机器学习基石 --PLA
本文是《机器学习基石》第二讲 Learning to Answer Yes/No 课程的笔记。主要介绍了机器学习的基本概念，以及感知机及其训练算法 PLA。
机器学习的基本概念
该讲以根据客户的特征来决定是否给客户发放信用卡的例子引出了机器学习要解决的问题：对于我们的问题，存在着一个未知的理想目标函数 \(f\) 能够满足我们的决策需求 (在该例子中就是根据给定用户的特征，输出是否给用户发放信用卡)，但是这个函数是未知的，我们只能从观测到的数据集 \(D\) 中通过算法 \(A\) 提取出一个近似的函数 \(g\) 来逼近理想的目标函数 \(f\)。而当选定了算法 \(A\) 后，选取 \(g\) 的集合 \(H\) 实际上也确定了 (例如目标函数是线性或非线性的)。
下图展示了上面提到的过程
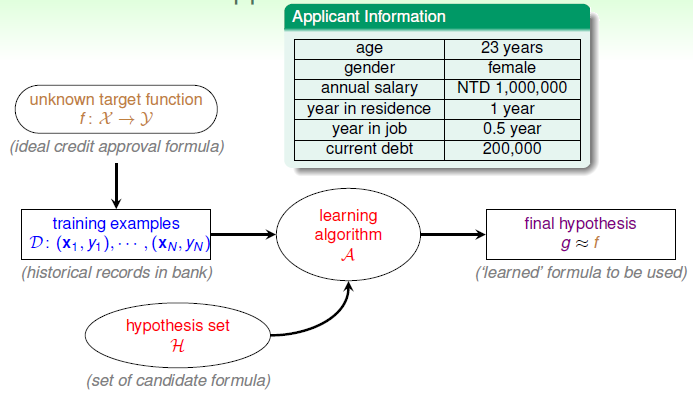
从上面概括了关于机器学习中的基本过程。但是在实际中通过机器学习解决问题的过程往往是的论述可知，机器学习中首先需要确定目前的一个问题，然后根据问题提出假设并依照假设去搜集数据，然后对数据进行特征提取、转换等，接着尝试通过不同算法去建模并验证。在这门课程中往往更关心数据特征的提取以及不同算法的研究，这固然很重要，但是实际中确认问题以及搜集相应的数据也是一个非常重要的步骤，不可忽视。
下面要介绍这门课程的第一个算法：
感知机
感知机是神经网络的基础，与线性回归（Linear Regression），逻辑回归（Logistics Regression）等模型也非常类似，是一种非常典型的线性模型。
原始的感知机算法用于解决二分类问题，其思想如下：假设样本有 \(d\) 个特征，但是每个特征的重要性不一样，因此各个特征的权重也不一样，对其进行加权后得到的总和假如大于某个阈值则认为归为其中一类，反之归为另一类。如在信用卡的例子中，通过感知机有如下的结果
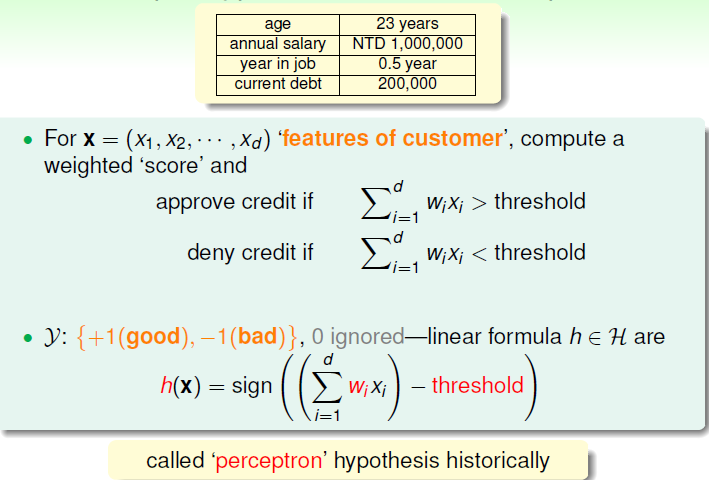
将上面的化为常数项，即可将得到更一般的表达形式如下
上面的 \(w\) 和 \(x\) 均是一个列向量。
PLA
上面只是说明了感知机这一算法的基本模型，但是感知机还要通过学习才能对样本进行正确的分类，这个学习的过程就是我们下面要讲的 PLA (Perceptron Learning Algorithm)。PLA 的过程如下
1）随机初始化参数 \(w\) 2）利用参数 \(w\) 预测每个样本点的值并与其实际的值比较，对于分类错误的样本点 \((x_n, y_n)\)，利用公式 \(w = w + y_nx_n\) 更新参数 \(w\) 的值 3）重复上面的过程直到所有的样本点都能够被参数 \(w\) 正确预测。
对于某个被预测错误的样本点，参数 \(w\) 更新的过程如下所示
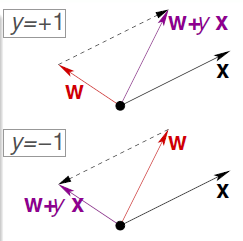
注意上面的算法的前提是所有的样本点都必须线性可分，假如样本点线性不可分，那么 PLA 按照上面的规则会陷入死循环中。如下是线性可分与线性不可分的例子)
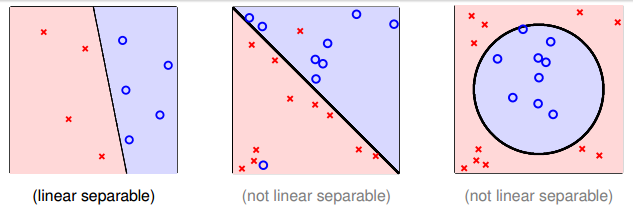
收敛性
上面提到只有当所有的样本均为线性可分时，PLA 才能将所有的样本点正确分类后再停下了，但是这仅仅是定性的说明而已，并没有严格的数学正面来支撑其收敛性，下面要讲的便是通过数学证明来说明 PLA 算法的收敛性。
建议中通过下面两页 PPT 来说明 PLA 的收敛性
上面讲的是随着参数 \(w\) 的更新，\(w_f^Tw_{t+1}\) 的值越来越大，也就是两者越来越相似（衡量两个向量相似性的一种方法就是考虑他们的内积，值越大，代表两者约接近，但是这里还没对向量归一化，所以证明并不严格，但是已经说明了两者具有这个趋势，下面是更严格的过程）
上面似乎只是说明了经过 T 次的纠错，\(w_t\) 的值会限制在一个范围内，但是并没有给出最终结论 \[\frac{w_f}{||w_f|| }\frac{w_T}{||w_T||} \ge \sqrt{T} * constant\] 的证明过程，因此这里对其推导过程进行描述。(注：这里的 \(w_f\) 是不变的，因此 \(w_f\) 与 \(w_f^T\) 是一样的)
假设经过了 T 次纠错，那由第一张 PPT 可知 \[\begin{align} w_f^Tw_T \ge w_f^Tw_{T-1} + \min_n y_nw_f^Tx_n \ge T\min_n y_nw_f^Tx_n \end{align}\]
而由第二张 PPT 可知
\[\begin{align}||w_T||^2 \le ||w_{T-1}||^2 + \max_n||x_n||^2 \le T\max_n||x_n||^2\\ ||w_T|| \le \sqrt{T} \max_n||x_n||\end{align}\]
综合上面的两条式子有
\[\begin{align} \frac{w_f^T}{||w_f^T||}\frac{w_T}{||w_T||} \ge \frac{T\min_n y_n^Tw_f^Tx_n}{||w_f^T||\sqrt{T} \max_n||x_n||} = \sqrt{T} \frac{\min_n y_n\frac{w_f^T}{||w_f^T||}x_n}{\max_n||x_n||} = \sqrt{T} * constant \end{align}\]
因此上面的命题得证。至此，已经可知道犯错误的次数 T 是受到某个上限的约束的。下面会给出这个具体的上限是多少。
又因为 \[1 \ge \frac{w_f^T}{||w_f^T||}\frac{w_T}{||w_T||} \ge \sqrt{T} * constant\\\ \frac{1}{constant^2} \ge T\]\[\begin {align} 即犯错的次数的上限为 $\frac {1}{constant^2} $, 假设令 $$\begin {align} \max_n||x||^2 = R^2, \rho = \min_n y_n\frac {w_f^T}{||w_f^T||} x_n \end {align}\]\[ 则有 \]\[\begin{align} T \le \frac{R^2}{\rho^2} \end{align}\]$$
这也说明了 PLA 会在有限步内收敛，而这也是后面的练习题里面的答案。
优缺点及改进
PLA 的优点和缺点都非常明显，其中优点是简单，易于实现，但是缺点是假设了数据是线性可分的，然而事先并无法知道数据是否线性可分的。正如上面提到的一样，假如将 PLA 用在线性不可分的数据中时，会导致 PLA 永远都无法对样本进行正确分类从而陷入到死循环中。
为了避免上面的情况，将 PLA 的条件放宽一点，不再要求所有的样本都能正确地分开，而是要求犯错的的样本尽可能的少，即将问题变为了 \[arg\min_w \sum_{n=1}^{N} 1\lbrace y_n \ne sign(w^Tx_n) \rbrace\]
这个最优化问题是个 NP-hard 问题，无法求得其最优解，因此只能求尽可能接近其最优解的近似解。讲义中提出的一种求解其近似解的算法 Pocket Algorithm。其思想就是每次保留当前最好的 \(w\), 当遇到错误的样本点对 \(w\) 进行修正后，比较修正后的 \(w\) 与原来最好的 \(w\) 在整个样本点上的总体效果再决定保留哪一个，重复迭代足够多的次数后返回当前得到的最好的 \(w\)。