《ImageNet Classification with Deep Convolutional Neural Networks》阅读笔记

发表于 标签 ，

ImageNet Classification with Deep Convolutional Neural Networks 这篇论文可以说是多层 CNN 用在图像领域的首次尝试（此前的 LeNet 也将 CNN 用在手写数字的识别上，但是没有用到连续多层 CNN）。文中提出的网络模型 AlexNet (设计者的名字叫 Alex) 在 ImageNet 2010、2012 年的比赛上取得的效果远远地优于传统方法，这篇文献最重要的工作是设计并验证了这样一个有多层卷积层的网络的有效性，对学术界和工业界的影响都很大。

本文主要介绍这篇文章中提出的网络模型 AlexNet，以及其他涉及到的一些知识，主要的介绍的内容有：CNN 的基础知识，AlexNet 的设计，训练和效果，以及对网络泛化（generalization）性能的一些探讨。

CNN 简介

CNN 全称是 Convolutional Neural Network，翻译做卷积神经网络，类似于我们常见的神经网络，CNN 也是一层一层连接起来的。顺便一提，这种 layer by layer 的网络叫做 feed-forward network，特点是无环，以区别于贝叶斯网络这种有环的网络

但是与传统的多层神经网络不同点在于，组成 CNN 的各个网络层不是常见的神经网络的里的网络层，而是由以下四种特殊的网络层组成

  1. 卷积层 (convolutional layer)
  2. 池化层 (pooling layer)
  3. ReLU 层 (ReLU layer)
  4. 全连接层 (fully connected layer)

下面分别介绍各个层的具体结构与作用

卷积层 (Convolutional layer)

卷积层是 CNN 中最重要的层，也是 CNN 名称的来源，卷积层里面有几个重要概念：核（kernel/filter)、卷积（convolution）、输出（activation map）。对照下图可以比较清晰的理解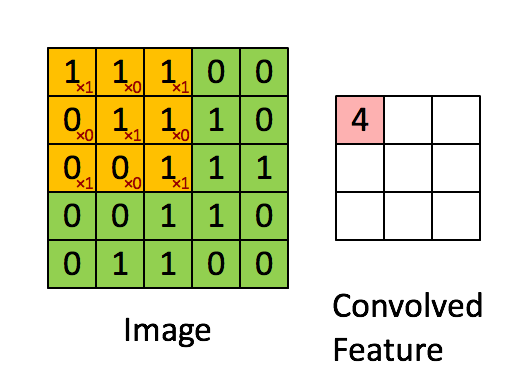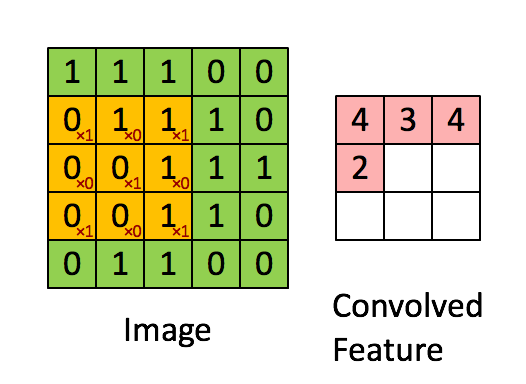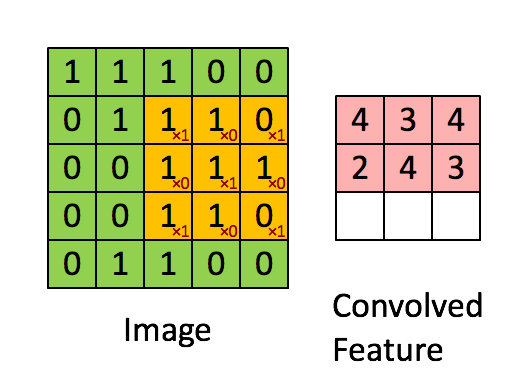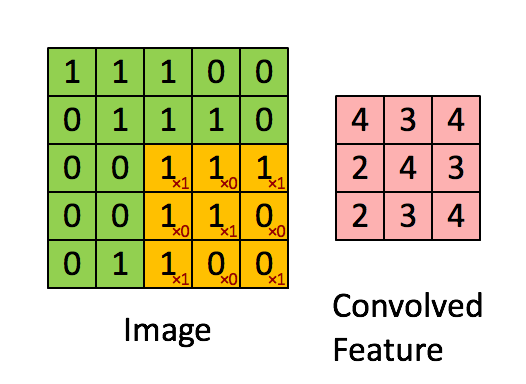

convolutional layer

核（kernel/filter): 移动的橙色正方形 卷积（convolution）：kernel 和 image 相应区域的点积 输出（activation map）：卷积的输出，图中的粉色区域（convolved feature）

卷积层的作用可以理解为特征抽取，这种设计来源于人脑里面的机制，但是我们也能够直观地理解这类操作的意义，假设说我们现在要观察一幅图像，往往是从左到右，从上到下来观察的，而相邻的区域往往具有相似性，对于小面积区域（也就是 kernel 覆盖的区域）可以用更少的数据来概括这部分的特征。

上面的图像只用了一个 kernel，我们将其看做是一个人观察这张图片得到的信息，那假如有更多的人观察这张图片，并将所有人观察到的信息综合起来，得到的信息是否会更加完备呢？答案是肯定的，这就涉及到了多个 kernel 的情况，具体如下图所示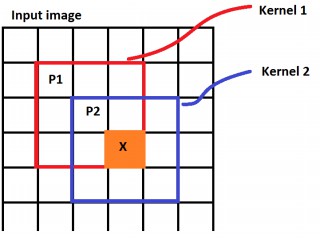

multiple_kernel.jpg-16.2kB

除了多个 kernel，图片也会有多个 channel，上图显示的 input image 只有一个 channel，但是实际中用于分类的图片往往是 RGB 图片，有 3 个 channel，分别是 red， blue，green，如下图所示

RGB channels

因此当输入的图片有多个 channel，并且用多个 kernel 去进行卷积的时候，过程会如下图所示（来源）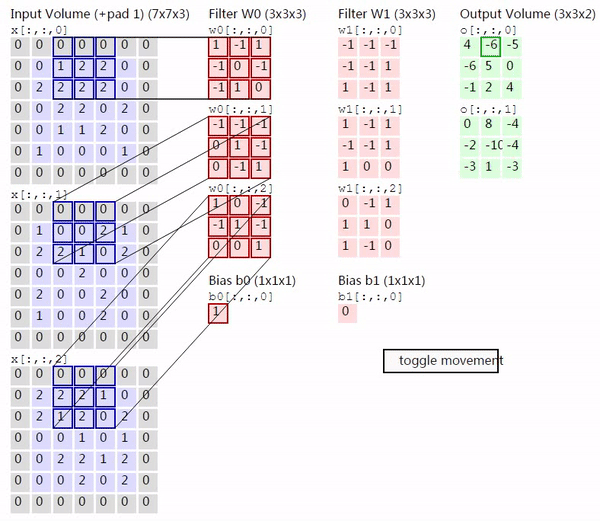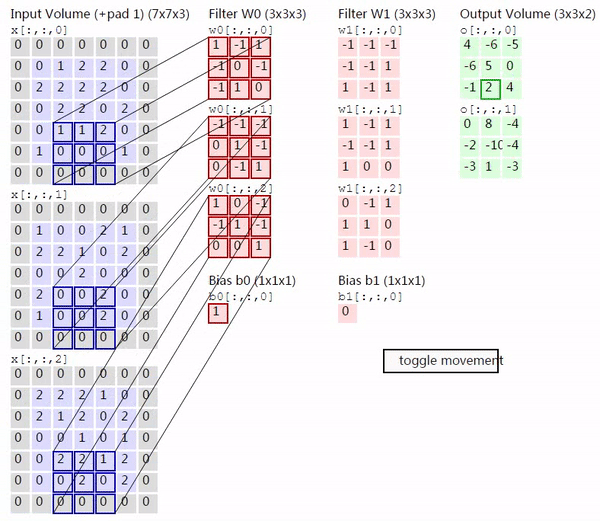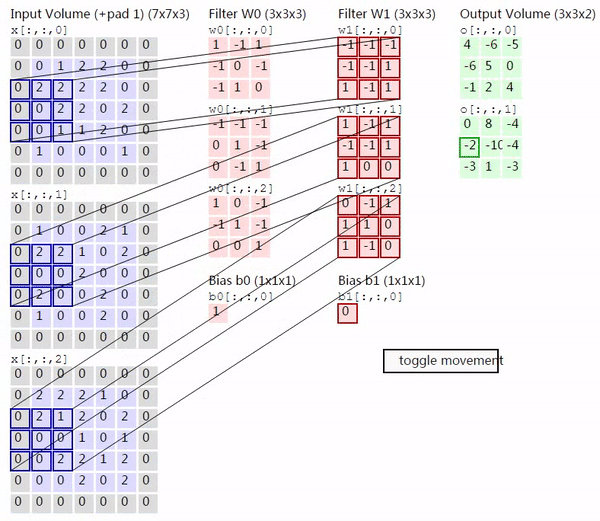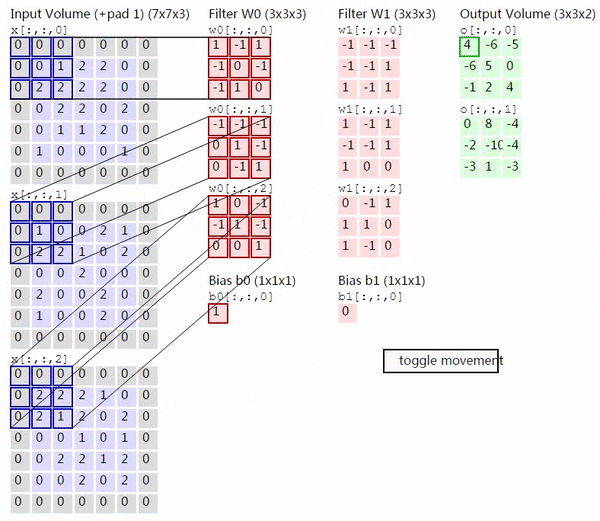

convolutional network

上图的左边是 input image 的三个 channel，中间是两个 kernel，右边是输出的两个 activation map。对于有多个 channel 的情况，每个 kernel 就不再是二维的，而是三维，除去表示 kernel 大小的两个维度，剩下的一个维度也叫深度，大小就是输入的 channel 的大小。将从各个 channel 得到的值加起来，就得到了对应的 activation map 相应位置的输出。这里需要注意的的是，无论输入有多少个 channel，每个 kernel 最终只产生一个 activation map。

池化层 (pooling layer)

池化类似于一种下采样（down sampling), 目的是要较少参数数量和计算量，如下所示是一个 max polling 的例子，其步长（stride）为 2，kernel 为 2 X 2。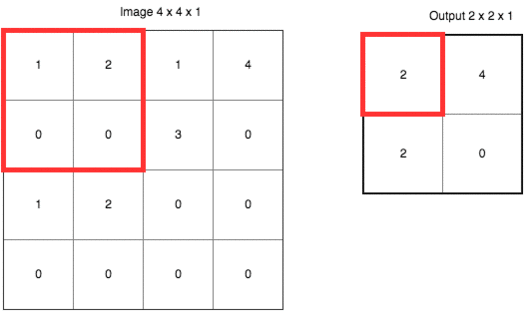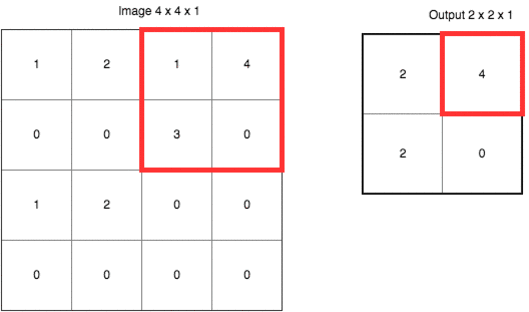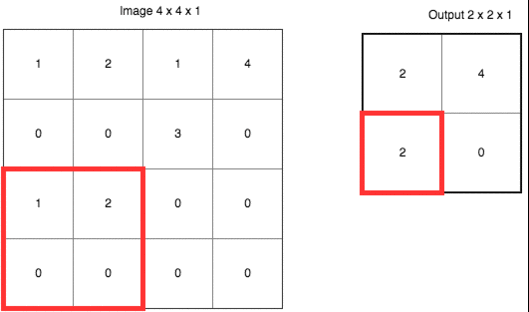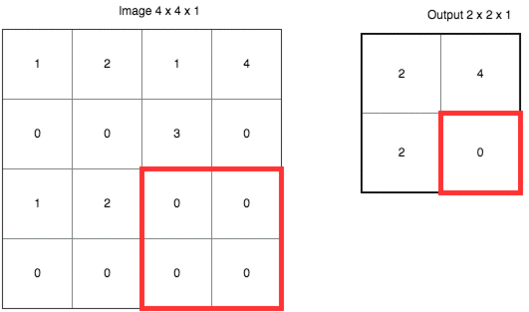

max pooling

max pooling 指的是每次取 kernel 中的最大值最为输出，除了 max pooling，还有 average pooling 等其他方式。除了上面提到的减少参数数量和计算量，池化还可以避免过拟合。

当上面的步长改为 1 后，kernel 移动过的区域会有重叠，我们称之为 overlapping pooling，如下图所示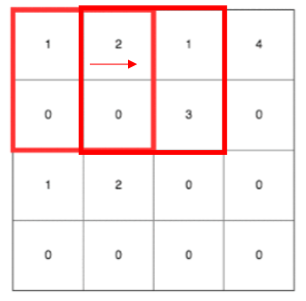

overlapping pooling

ReLU 层 (ReLU layer)

ReLU 的全称是 Rectified Linear Units，从严格意义上来讲，ReLU 只是一个激活函数，而不能称之为一个层。其函数表达式为 \(f(x) = max(0, x)\)，其图像如下所示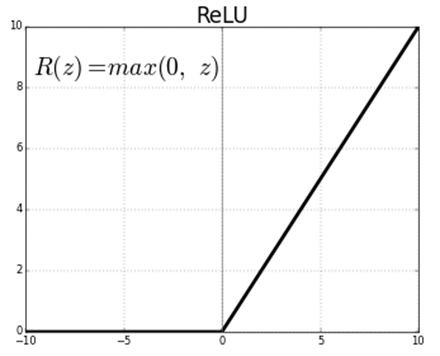

ReLU

ReLU 的主要作用是提升整个网络的非线性判别能力。关于选择 ReLU 作为激活函数而不是 sigmoid 或 tanh，后面会有详细说明。

全连接层 (fully connected layer)

全连接层就是我们常见的神经网络中的网络层，每个神经元都与前面或后面的各个神经元有连接，如下图所示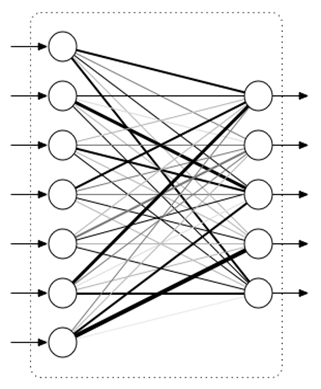

fully connected layer

由于全连接层的参数过多，在 CNN 中全连接层往往是作为最后几层用于输出。

网络的设计

上面介绍的四类 layer 是构成这篇论文中的 CNN 网络四种 layer，下面介绍论文中的 CNN 网络的结构及其特点。

网络结构总览

文中提出的 CNN 网络结构如下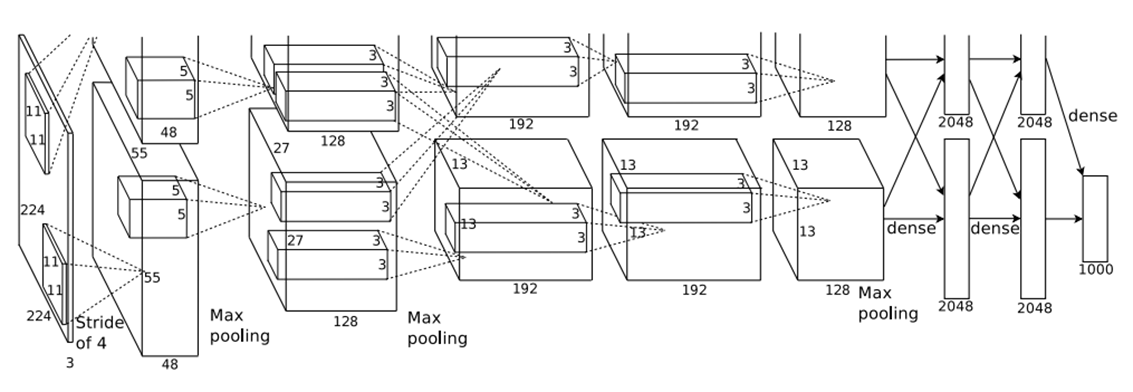

Alexnet

上图有以下几个特点

  1. 由 5 层卷积层 + 3 层全连接层构成，并且整个网络在两个 GPU 上训练
  2. 在第 1、2、5 层卷积层后添加了最大池化的操作
  3. 在每层卷积层和全连接层后都有 ReLU 激活函数

上图中网络就是 AlexNet，网络结构可以这样理解，首先上下两部分表示网络在两个 GPU 上训练，前五层表示 5 层卷积层，后三层表示 3 层全连接层；而立方体（最左边的是输入的图像，这里不算入）表示每层卷积层的输出，立方体里面的小立方体表示 kernel 的大小。

第一层卷积层采用了 48+48 共 96 个 kernel，输入的图像有三个 channel，但是前面提到无论有多少个 channel，一个 kernel 只会产生一个 activation map，所以图中的第一个立方体 48 表示输出的 48 个 activation map，而这 48 个 activation map 作为第二层卷积层的输入又成为了 48 个 input channels，依次类推，第二层卷积层采用了 128+128 共 256 个 kernel。

网络的特点

这个网络有三个特点并没有在上图中并不是非常显式地展示出来：分别是 ReLU Nonlinearity、Local Response Normalization 和 Overlapping Pooling。

ReLU Nonlinearity

ReLU 在前面已经简单地进行了介绍，这里要讨论的是为什么采用了 ReLu 作为激活函数而不是 其他的如 sigmoid 或 tanh。主要原因是 ReLU 能够更快地收敛，因为其能够在一定程度上避免梯度消失（vanishing gradient ）的现象。

要解释这个原因首先需要看看这三个函数的图像（ReLU 的图像上面已经给出）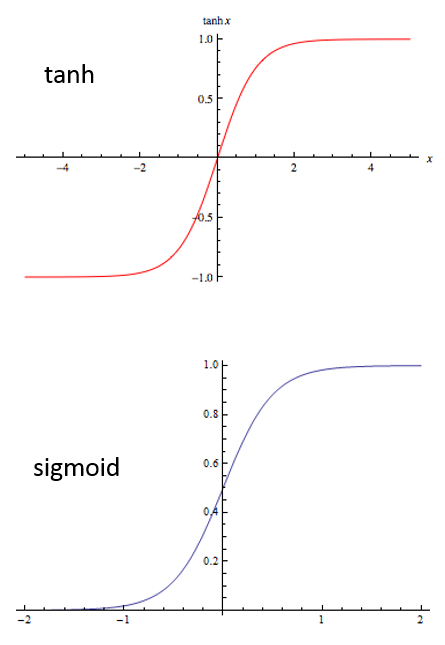

tanh 和 sigmoid

这两个激活函数的图像非常相似，均是两边平，中间陡。当通过反向传播（backpropgation）训练时，需要通过链式法则求出总的梯度，而当激活值很大或很小的时候，也就是对应到上面图像两边平缓的地方是，对这两个激活函数的求导结果几乎为 0， 从而导致相乘得到的总的梯度也几乎为 0，错误不能有效地传播到前面的层，修正前面层的参数。这种现象就称为梯度消失。

而对于 ReLU 函数，当激活值小于 0 的时候，也存在着相同问题，而且这时候导数完全是 0；但是大于 0 的时候 ReLU 的导数总是 1，因此大于 0 的时候不存在梯度消失的现象。也有人说当激活值小于 0 的时候会带来稀疏性的好处。

Local Response Normalization

Local Response Normalization 指的是对网络中经过 ReLU 层输出的结果进行正规化， 其正规化的公式如下所示：

\[\begin{align} b_{x,y}^i = a_{x,y}^i/(k + \alpha \sum_{j=\max(0, i-n/2)}^{\min(N-1, i+n/2)}(a_{x,y}^j)^2)^{\beta} \end{align}\]

上式中的 \(a_{x,y}^i\) 表示第 \(i\) 个 kernel 在位置 \((x,y)\) 的原始输出，而 \(b_{x,y}^i\) 表示正规化后的输出，\(N\) 表示所有 kernel 的数目。上式表明对某个 kernel 在某个位置的输出的正规化利用了与这个 kernel 相邻的 \(n\) 个 kernel 在相同位置的值进行。

而其他参数 \(k, n, \alpha, \beta\) 则是通过 cross-validataion 获得的参数，Local Response Normalization 分别被应用到第一层和第二层卷积层，文章里说这种方法分别将 top-1 error 和 top-5 error 降低了 1.4% 和 1.2%。

Overlapping Pooling

这个机制我们在前面谈到池化层的时候已经提到，文章里说这种方法分别将 top-1 error 和 top-5 error 降低了 0.4% 和 0.3%。

网络的训练

目标函数

文章中的问题是一个图像多分类的问题，多分类问题有若干种方法，在神经网络中最常用的就是 softmax

单纯从数学的角度来讲，softmax 只是一种向量变换方式，假设现在有一个长度为 \(k\) 的向量 \(z = (z_1,...z_k)\), 对其进行 softmax 变换后得到向量 \(\sigma(z)\), 其变换公式如下

\[\begin{align} \sigma(z)_j = \frac{e^{z_j}}{\sum_{l=1}^k e^{z_l}}~~~(j=1,...k) \end{align}\]

变换后的向量 \(\sigma(z)\) 有一个重要特征，就是所有元素之和加起来为 1；从概率论的角度来考虑，很自然地可以将这个向量作为属于各个分类的一个概率分布，选择值最大的那个项对应的分类作为其分类。

这种 “自然” 也是有数学支撑的，实际上，softmax 的这个特性可以从 Generalized Linear Model 中推导出来。这里就不详细展开论述了。

有了概率分布，很自然地一个想法就是做极大似然估计，如下是一个 \(k\) 分类问题中，最大化 \(m\) 个 sample 的联合概率分布，其中 \(1 \lbrace . \rbrace\) 的含义为 \(1 \lbrace True \rbrace = 1, 1 \lbrace False \rbrace = 0\)，如 \(1 \lbrace 2=2 \rbrace = 1, 1 \lbrace 2=3 \rbrace = 0\)

\[\begin{align} \max \sum_{i=1}^{m} \sum_{j=1}^{k} 1 \lbrace y^{(i)} = j \rbrace \log \frac{e^{z_j}}{\sum_{l=1}^k e^{z_l}} \end{align}\]

在其前面添加一个负号和一个常数 \(\frac{1}{m}\) 可以将其转为如下的极小化问题

\[\begin{align} \min -\frac{1}{m} \sum_{i=1}^{m} \sum_{j=1}^{k} 1 \lbrace y^{(i)} = j \rbrace \log \frac{e^{z_j}}{\sum_{l=1}^k e^{z_l}} \end{align}\]

实际上，上面要最小化的目标函数是交叉熵损失（cross-entropy error），这个目标函数也可以通过交叉熵的定义推导出来。

训练算法

上面得到的最后是一个无约束的最优化问题，对于这类最优化问题有多种方法可用，其中最常用的是随机梯度下降（Stochastic Gradient Descent），但是这里没有用原始的 SGD， 而是采用了带有 momentum, weight decay 和 mini-batch 的 SGD。

momentum, weight decay 和 mini-batch 是三个非常重要的概念，这里简单说明他们的作用

momentum 指的是每次更新参数的梯度除了用当前迭代得到的梯度，还要加上前一次迭代得到的梯度，起作用是为了加快收敛，避免局部最优（如果问题非凸的话）

weight decay 实际上是 L2 regularization 微分后得到的项，其目的是为了防止过拟合。

mini-batch 则是指每个更新时不仅采用一个样本，而是采用多个样本，这种方法介于 BGD 和 SGD 之间。

其更新的规则如下所示，参数 ，\(v_i\) 被称作 momentum variable， $- 0.0005 w_i $ 是 weight decay 项，\(<\frac{\partial L}{\partial w}|_{w_i}>_{D_i}\) 则是从 mini-batch 为 \(D_i\) 中得到的 gradient， \(\epsilon\) 为步长。

\[\begin{align} &v_{i+1} = 0.9v_i - 0.0005 \epsilon w_i - \epsilon <\frac{\partial L}{\partial w}|_{w_i}>_{D_i}\\\ &w_{i+1} = w_i + v_{i+1} \end{align}\]

多 GPU 训练

前面已经提到了整个网络在两个 GPU 上训练， 原因是 GPU 能够并行的处理数据，训练速度较快，而同时一个 GPU 限制了模型的大小，因此用到了两个，两个 GPU 是并行的训练网络的，除了在第三层的卷积层两个 GPU 交换了数据用于 cross validation。与一个 GPU 训练的模型相比，两个 GPU 训练的模型分别将 top-1 error 和 top-5 error 降低了 1.7% 和 1.2%。

防止过拟合

为了防止过拟合，文章采用了两种方法，data augmentation 和 dropout。

data augmentation

data augmentation 指的是如何从提供的数据集中得到更多的数据，文中也采用了两种途径，其中一种是从原始图像（大小为 256 × 256）中抽出多个大小为 224 × 224 的块作为图像，因此一幅原始图像能够生成多个图像；另外一种途径就是在原始图像的像素上加上通过 PCA 从图像中抽取出来的信息，从而生成新的图像。这两种方法将 top-1 error 降低了 1%。

dropout

droupout 指的是每个神经元每次传递值时只有 50% 的概率工作，如下图所示，灰色的神经元指的是该神经元并没有工作。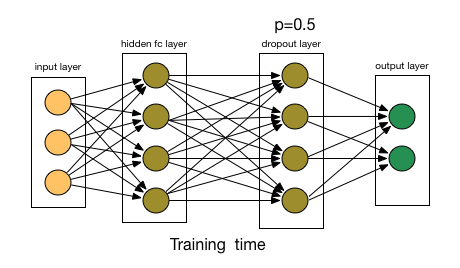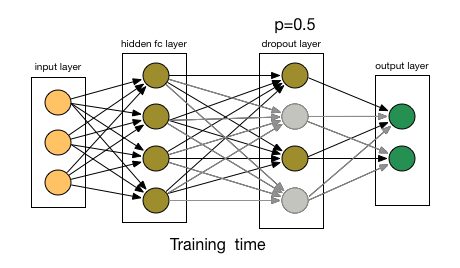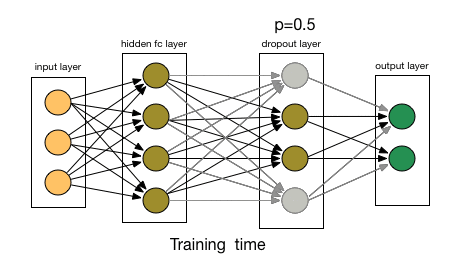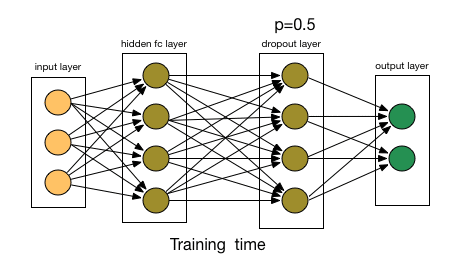

dropout

这种方法的好处是降低了神经元间的依赖性，使得每个神经元更加 robust。droupout 被添加在第一和第二层全连接层中。

网络的效果

文中采用的数据集是 ImageNet，这是一个有着约 14 million 张 labeled image 的图片集，每一年通过这个数据集会举办一次名为 ImageNet Large-Scale Visual Recognition Challenge (ILSVRC) 的比赛，就是一个图片多分类比赛，文中展示了上面提到的 cnn 网络在 2010 年和 2012 年比赛中的表现结果，结果如下所示

2010 年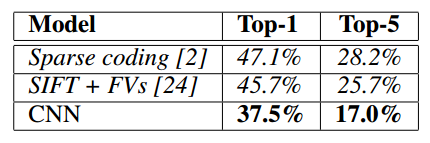

201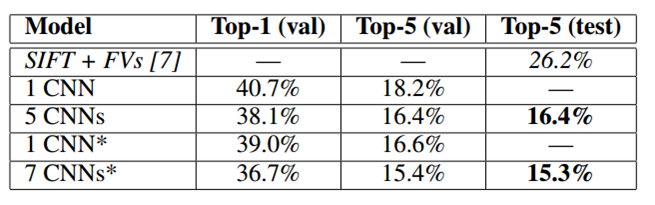0

2012 年 2012

其中 2012 年的表格中 5 CNNs 表示用了 5 个 CNN 做投票 ensemble 后的效果，CNN* 表示在原来的 5 层卷积层的基础上再增加一层卷积层。可以看到 CNN 所得到的结果要远远优于第二名的，而这也是当年这篇文章震惊了学术界和工业界的原因。

网络泛化能力的探讨

从上面的论述中可知，我们将多个卷积层和全连接层连在一起，然后加上 pooling，dropout 等操作，就构建了一个取得非常好效果的网络，很自然我们会问，这个网络为什么能够取得这么好的效果？或者说这个网络的泛化能力为什么会这么好，是不是有什么保证了其泛化误差不会过大？

在统计机器学习中，有一个叫 VC dimension 的概念，用于描述模型的复杂度，这个概念中的 VC bound 为泛化误差约束了一个 bound，但是这个概念需要很复杂的数学推导，这里我们略去这些推导。只说一个 VC dimension 给我们揭示的一个很直观的概念：要取得较好的泛化能力，用于训练模型的样本数目应该至少是参数数目的 10 倍。

这个理论在统计机器学习的 svm 等模型中都得到了较好的验证，但是文中提出的网络有 60 million 的参数和 1.25 million 的样本，因此这个条件远远没得到满足。但是网路却取得了很好的效果，这样看来，VC dimension 这个理论并适用于这个网络，实际上，不仅仅是这个网络，VC dimension 在深度学习中多个网络中也不适用。

而这一点，也被 2017 ICLR 的最佳论文 Understanding deep learning requires rethinking generalization指出，下图是从这篇论文的 presentation 中抽取的一张图片。

4 networks

图中四个宠物小精灵代表了四个著名的网络，随着 p/n 值越来越大，也就是 “样本 / 参数” 的比值越来越小，越不满足 VC dimension 提出的条件，但是泛化的误差却越来越小。

这篇最佳论文还做了很多其他实验，这里就不详细展开，但是从这篇文章并没有从理论上说明了这个网络泛化误差小的理论依据，也就是没有提出在深度学习领域适用的 “VC dimension”，而这一工作将会是未来深度学习发展中非常重要和有意义的工作。