凸优化总结

之前曾写过一篇最优化课程总结， 涉及到的内容较多也较细。而在最优化中，凸优化是最为常见而又最为重要的，因为凸优化有一个良好的性质：局部最优是全局最优，这个性质使得我们不需要去证明解是否会收敛到全局最优，或者如何避免局部最优。因此凸优化有广泛应用，在优化问题不是凸的时候，往往也会尝试将其变为凸问题便于求解。本文着重讲凸优化，算是对之前写的文章的一个拓展和补充。

本文主要讲述下面内容，凸优化的概念以及凸优化中的三类常见解法：梯度类方法，对偶方法和 ADMM 方法。

凸集，凸函数与凸优化

凸集

凸集的定义非常清楚

对于集合 \(K\) ，\(\forall x_1,x_2 \in K\), 若 \(\alpha x_1 + (1-\alpha)x_2 \in K\), 其中 \(\alpha \in [0,1])\), 则 \(K\) 为凸集

即集合中任意两点的连线均在凸集中，如在下图中左边的是凸集而右边的不是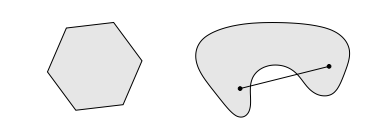

有时候需要对某个凸集进行放缩转换等操作，对凸集进行以下操作后，得到的集合依然是凸集

1. 凸集的重叠（intersection）部分任然为凸集
2. 若 \(C\) 为凸集，则 \[aC+b = \lbrace ax+b , x \in C, \forall a, b\rbrace\] 也为凸集
3. 对于函数 \(f(x) = Ax+b\), 若 \(C\) 为凸集，则下面得到的转换也为凸集，注意这里的 \(A\) 是矩阵 \[f(C) = \lbrace f(x):x\in C\rbrace\] 而当 \(D\) 是一个凸集的时候，下面得到的转换也是凸集 \[f^{-1}(D) = \lbrace x: f(x)\in D\rbrace\] 这两个转换互为逆反关系

常见的凸集有下面这些 (下式中 \(a, x, b\) 均为向量，\(A\) 为矩阵)

• 点（point）、线（line）、面（plane）
• norm ball: \(\lbrace x: ||x|| \le r\rbrace\)
• hyperplane: \(\lbrace x: a^Tx=b\rbrace\)
• halfspace: \(\lbrace x: a^Tx \le b\rbrace\)
• affine space: \(\lbrace x: Ax = b\rbrace\)
• polyhedron: \(\lbrace x: Ax < b\rbrace\)

polyheron 的图像为

凸函数

凸函数的定义如下

设 \(f(x)\) 为定义在 n 维欧氏空间中某个凸集 S 上的函数，若对于任何实数 \(\alpha(0<\alpha<1)\) 以及 S 中的任意不同两点 \(x\) 和 \(y\)，均有 \[f(\alpha x+ (1-\alpha)y) \le \alpha f(x) + (1-\alpha)f(y)\] 则称 \(f(x)\) 为定义在凸集 S 上的凸函数

凸函数的定义也很好理解，任意两点的连线必然在函数的上方，如下是一个典型的凸函数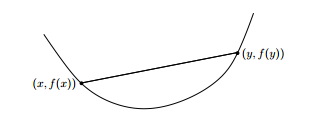

严格凸 (strictly convex) 与強凸 (strongly convex)

• 严格凸指的是假如将上面不等式中的 \(\le\) 改为 \(\lt\)， 则称该函数为严格凸函数。
• 严格凸指的是 \(\forall m > 0, f - \frac{m}{2}||x||_2^2\) 也是凸的，其含义就是该凸函数的 “凸性” 比二次函数还要强，即使减去一个二次函数还是凸函数

凸函数有几个非常重要的性质，对于一个凸函数 \(f\), 其重要性质 1. 一阶特性（First-order characterization）： \[f(y) \ge f(x) + \nabla f(x)(y - x)\] 2. 二阶特性（Second-order characterization）： \[\nabla^2f(x) \succeq 0\] 这里的 \(\succeq 0\) 表示 Hessian 矩阵是半正定的。 3. Jensen 不等式（Jensen’s inequality）：\[f(E(x)) \le E(f(x))\] 这里的 \(E\) 表示的是期望，这是从凸函数拓展到概率论的一个推论，这里不详细展开。 4. sublevel sets，即集合 \(\lbrace x:f(x) \le t\rbrace\) 是一个凸集

其中，一阶特性或二阶特性是一个函数为凸函数的充要条件，通常用来证明一个函数是凸函数。

常见的凸函数有下面这些

• 仿射函数 (Affine function): \(a^Tx + b\)

• 二次函数 (quadratic function), 注意这里的 \(Q\) 必须为半正定矩阵: \(\frac{1}{2}x^TQx + b^Tx+c(Q \succeq 0)\)

• 最小平方误差 (Least squares loss): \(||y-Ax||_2^2\) (总是凸的，因为 \(A^TA\) 总是半正定的)

• 示性函数（Indicator function）：\[I_C(X) = \begin{cases} 0&x \in C\\\ \infty & x \notin C\end{cases}\]

• max function: \(f(x) = max \lbrace x_1,...x_n \rbrace\)

• 范数（Norm）：范数分为向量范数和矩阵范数，任意范数均为凸的，各种范数的定义如下

向量范数

0 范数：$||x||_0 $= 向量中非零元素的个数 1 范数： \(||x||_1 = \sum_{i=1}^n |x_i|\) \(p\) 范数：\(||x||_p = (\sum_{i=1}^nx_i^p)^{1/p}~~(p > 1)\) 无穷范数: \(||x||_{\infty} = max_{i=1,...n} |x_i|\)

矩阵范数 > 核 (nuclear) 范数: \(||X||_{tr} = \sum_{i=1}^{r}\sigma_i(X)\) , (\(\sigma_i(X)\) 是矩阵分解后的奇异值，核范数即为矩阵所有奇异值之和) > 谱（spectral）范数：\(||X||_{op} = max_{i=1,...r}\sigma_i(X)\), 即为最大的奇异值

凸优化

对于下面的优化问题

\[\begin{align} &\min_x\quad f(x)\\\ &\begin{array}\\\ s.t.&g_i(x) \le 0,~i=1,\ldots,m\\\ &h_j(x)=0,~j=1,\ldots,r \end{array} \end{align}\]

当 \(f(x), g_i(x)\) 均为凸函数， 而 \(h_j(x)\) 为仿射函数（affine function）时，该优化称为凸优化，注意上面的 \(\min\) 以及约束条件的符号均要符合规定。

凸优化也可以解释为目标函数 \(f(x)\) 为凸函数而起约束围成的可行域为一个凸集。

常见的一些凸优化问题有：线性规划（linear programs），二次规划（quadratic programs），半正定规划（semidefinite programs），且 \(LP \in QP \in SDP\), 即后者是包含前者的关系。

线性规划问题一般原型如下 (\(c\) 为向量，\(D,A\) 为矩阵)

\[\begin{align} &\min_x\quad c^Tx\\\ &\begin{array}\\\ s.t.&Dx \le d\\\ &Ax=b \end{array} \end{align}\]

二次规划问题一般原型如下（要求矩阵 \(Q\) 半正定）

\[\begin{align} &\min_x\quad \frac{1}{2}x^TQx+c^Tx\\\ &\begin{array}\\\ s.t.&Dx \le d\\\ &Ax=b \end{array} \end{align}\]

而半正定规划问题一般原型如下 (\(X\) 在这里表示矩阵) \[\begin{align} &\min_X\quad CX\\\ &\begin{array}\\\ s.t.&A_iX \le b_i, i=1,...m\\\ &X \succeq 0 \end{array} \end{align}\]

梯度类方法

梯度类方法是无约束优化中非常常用的方法，其依据的最根本的事实就是梯度的负方向是函数值下降最快的方向。但是常用的 gradient descent 必须要求函数的连续可导，而对于某些连续不可导的问题（如 lasso regression），gradient descent 无能为力，这是需要用到 subgradient descent 和 proximal gradient descent.

gradient descent

梯度下降法的迭代公式为 \[x^{(k)} = x^{(k-1)} - t_k\nabla f(x^{(k-1)} )\]

上式中上标 \((k)\) 表示第 \(k\) 次迭代，而 \(t_k\) 表示步长，\(\nabla f(x^{(k-1)} )\) 表示在点 \(x^{(k-1)}\) 的梯度。

这里对于梯度下降主要讨论其步长选择的问题， 最简单直接的方式是固定每次的步长为一个恒定值，但是如果步长过大或过小时，可能会导致结果难以收敛或者收敛速度很慢。因此提出了可变长步长的方法，可变长步长的方法指的是根据每次迭代依照一定的规则改变步长，下面介绍两种：backtracking line search 和 exact line serach。

backtracking line search

backtracking line search 需要先选择两个固定的参数 \(\alpha, \beta\), 要求 \(0 < \beta < 1, 0<\alpha<1/2\)

每次迭代的时候，假如下式成立

\[\begin{align} f(x - t\nabla f(x)) > f(x) - \alpha t||\nabla f(x)||_2^2 \end{align}\]

则改变步长为 \(t = \beta t\), 否则步长不变。

这种方法的思想是当步长过大的时候 (即跨过了最优点)，减小步长，否则保持步长不变，如下式是一个简单的例子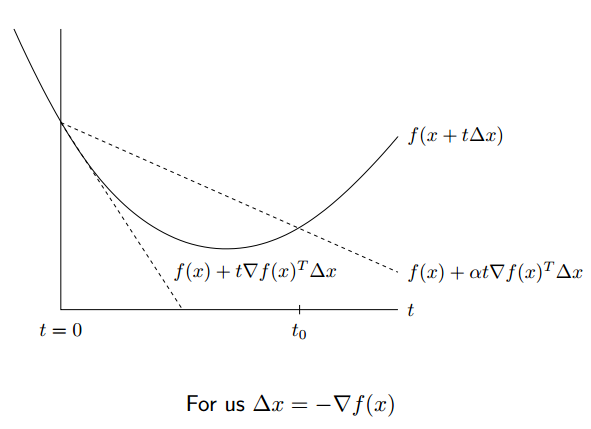

exact line serach

exact line serach 则是得到先计算出梯度 \(\nabla f(x^{(k-1)} )\), 然后代入下面的函数中，此时只有步长 \(t_k\) 是未知，因此可对 \(t_k\) 进行求导并令其为 0，求得的 \(t_k\) 即为当前的最优的步长，因为这个步长令当前迭代下降的距离最大。

\[\begin{align} f(x^{(k-1)} - t_k\nabla f(x^{(k-1)} )) \end{align}\]

这种方法也被称为最速下降法。

subgradient descent

subgradient 可以说是 gradient 的升级版，用于解决求导时某些连续不可导的函数梯度不存在的问题，我们知道，对于可微的凸函数有一阶特性，即

\[\begin{align} f(y) \ge f(x) + \nabla^T f(x)(y - x) \end{align}\]

加入将上面的 \(\nabla^T f(x)\) 换成 \(g^T\) 且不等式恒成立，则 \(g\) 被称为 subgradient，当函数可微时，\(\nabla f(x) = g\) ，但是若函数不可微，subgradient 不一定存在，下面是几个特殊函数的 subgradient 例子。

对于函数 \(f(x) = |x|\), 其图像如下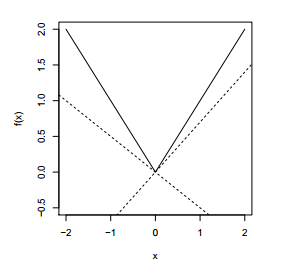

其 subgradient 为 \[g = \begin{cases}sign(x) &x \neq 0\\\ [-1,1] & x=0\end{cases}\]

对于函数 \(f(x) = ||x||_2\), 其图像如下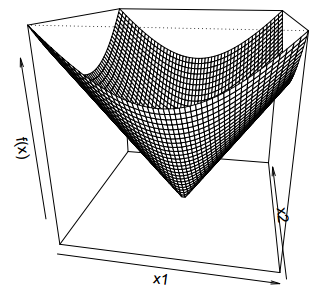

其 subgradient 为 \[g = \begin{cases} x/||x||_2&x \neq 0\\\ \lbrace z: ||z||_2 \le 1\rbrace & x=0\end{cases}\]

对于函数 \(f(x) = ||x||_1\), 其图像如下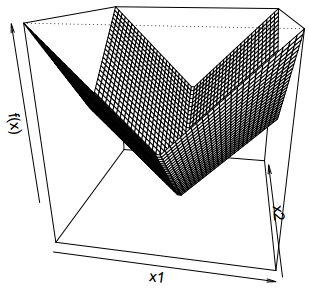

其 subgradient 为 \[g = \begin{cases} sign(x_i) &x_i \neq 0\\\ [-1,1] & x_i=0\end{cases}\]

对于两个相交的函数 \(f(x) = \max \lbrace f(x_1), f(x_2)\rbrace\), 设其函数图像如下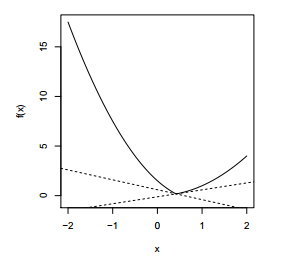

则其 subgradient 为 \[g = \begin{cases} \nabla f(x_1) &f(x_1) > f(x_2) \\\ \nabla f(x_2) &f(x_1) < f(x_2) \\\ [\min \lbrace \nabla f(x_1),\nabla f(x_2)\rbrace, \max \lbrace \nabla f(x_1), \nabla f(x_2)\rbrace] &f(x_1) = f(x_2)\end{cases} \]

而 subgradient descent 与 gradient descent 的不同地方就是当函数不可微的时候，将 gradient descent 中更新公式中的 gradient 换成 subgradient。下面看一个经典的 lasso regression 问题。

\[\begin{align} \min_{\beta \in \mathbb {R}^n} \frac{1}{2} ||y-\beta||_2^2 + \lambda ||\beta||_1~~(\lambda \ge 0) \end{align}\]

对目标函数求导并令其为 0，其中 \(||\beta||_1\) 项不可导，用前面提到的 subgradient 代替，则有以下等式

\[\begin{cases} y_i - \beta_i = \lambda sign(\beta_i) &\beta_i \neq 0\\\ |y_i - \beta_i| \le \lambda &\beta_i = 0 \end{cases}\]

则解可表示成

\[\beta_i = \begin{cases} y_i - \lambda & y_i > \lambda\\\ 0 &-\lambda \le y_i \le \lambda \\\ y_i + \lambda & y_i < -\lambda\end{cases}\]

上面实际上是简化了的 lasso regression， 因为更一般的 lasso 问题表示如下

\[\begin{align} \min_{\beta \in \mathbb {R}^n} \frac{1}{2} ||y-X\beta||_2^2 + \lambda ||\beta||_1~~(\lambda \ge 0) \end{align}\]

这时如果采用上面的解法，那么会得到

\[\begin{cases} X_i^T(y - X\beta) = \lambda sign(\beta_i) &\beta_i \neq 0\\\ |X_i^T(y - X\beta)| \le \lambda &\beta_i = 0 \end{cases}\]

上式并没有为这个 lasso 问题提供一个明确的解，这个问题可以通过下面要提到的 proximal gradient 进行求解，但是上面的式子一定程度上解释了 L1 regularization 的导致的参数的稀疏性的特点，从上面的表达式可知，只有当 \(X_i^T(y - X\beta) = \lambda sign(\beta_i)\) 时，对应的 \(\beta_i\) 才不为 0，而其他大多数的情况下 \(\beta_i\) 为 0.

proximal gradient descent

proximal gradient descent 也可以说是 subgradient 的升级版，proximal 通过对原问题的拆分并利用 proximal mapping，能够解决 subgradient descent 无法解决的问题（如上面的一般化 lasso 问题）。

一般来说，这类方法将目标函数描述成以下形式

\[\begin{align} f(X) = g(x) + h(x) \end{align}\]

上面的 \(g(x)\) 是凸且可微的， 而 \(h(x)\) 也是凸的，但是不一定可微。则 proximal gradient descent 的迭代公式为

\[\begin{align}x^{(k)} = x^{(k-1)} - t_kG_{t_k}(x^{(k-1)})\\\ G_{t}(x) = \frac{x - prox_{th}(x-t\nabla g(x))}{t}\\\ prox_{th}(x) = argmin_{z\in \mathbb {R}^n} \frac{1}{2t}||x-z||_2^2+h(z)\end{align}\]

上面 \(prox_{th}(x)\) 表示对函数 \(h\) proximal mapping。这里仅给出结论，证明过程略，接下来以上面没有解决的一般化的 lasso 问题为例讲述这种方法的应用。

\[\begin{align} \min_{\beta \in \mathbb {R}^n} \frac{1}{2} ||y-X\beta||_2^2 + \lambda ||\beta||_1~~(\lambda \ge 0) \end{align}\]

记 \(g(\beta) = \frac{1}{2} ||y-X\beta||_2^2, h(\beta) = \lambda ||\beta||_1\)

则有 \[\begin{align} prox_{th}(\beta) = argmin_{z \in \mathbb {R}^n} \frac{1}{2t}||\beta - z||_2^2+h(z) \end{align}\]

这个问题通过前面的 subgradient 方法已经解出来，结果为

\[z_i = \begin{cases} y_i - \lambda t & y_i > \lambda t\\\ 0 &-\lambda t \le y_i \le \lambda t\\\ y_i + \lambda t & y_i < -\lambda t\end{cases}\]

将上面的解记为 \(S_{\lambda t}(y)\), 同时 \(\nabla g(\beta) = - X^T(y-X\beta)\)

代取上面列出的 proximal gradient descent 列出的迭代公式，则 \(\beta\) 的迭代公式如下

\[\begin{align} \beta^{(k)} = S_{\lambda t}(\beta^{(k-1)} + t_kX^T(y-X\beta^{(k-1)})) \end{align}\]

其中 \(t_k\) 为步长。

这种方法之所以比 subgradient 方法更加一般化，是因为 \(prox_{th}(x)\) 对于绝大部分的 \(h\) 是易求的。

对偶方法与 KKT 条件

对偶理论在最优化中非常重要，其中具有代表性的两条定理是弱对偶定理和强对偶定理，弱对偶定理告诉了我们最优化的目标的上界 ( max 问题) 或下界 (min 问题)，而强对偶定理告诉了当 KKT 条件满足的时候，可以通过对偶问题的解推出原问题的解。

弱对偶条件总是成立，而强对偶需要在 Slater's condition 成立时才成立，该条件描述如下

对于优化问题

\[\begin{align} &\min_x\quad f(x)\\\ &\begin{array}\\\ s.t.&g_i(x) \le 0,~i=1,\ldots,m\\\ &h_j(x)=0,~j=1,\ldots,r \end{array} \end{align}\]

假如存在可行解 \(x'\) 使得 \(g_i(x') < 0(i=1,...m)\), 即不等式约束严格成立（注意同时等式约束也要成立，否则就不是可行解了），那么称 Slater's condition 成立，同时强对偶也成立。

线性规划对偶

对于形如下面的线性规划问题

\[\begin{align} &\min_x\quad c^Tx\\\ &\begin{array}\\\ s.t.&Ax = b\\\ &Gx \le h \end{array} \end{align}\]

其对偶问题为

\[\begin{align} &\min_{u,v}\quad -b^Tu - h^Tv\\\ &\begin{array}\\\ s.t.&-A^Tu - G^Tv = c\\\ & v \ge 0 \end{array} \end{align}\]

对于 LP 问题，其对偶的特殊性在于只要存在原问题存在可行解，那么 Slater's condition 一定成立，因此强对偶也成立.

LP 对偶问题的一个经典的例子是最大流 (max flow) 问题和最小割 (min cut) 问题.

拉格朗日对偶

对于更一般的非 LP 问题的对偶问题，需要用到拉格朗日对偶理论得到，并称该问题为拉格朗日对偶问题。

这个方法可以说是对求解等式约束的拉格朗日乘子法的一个推广。

对于下面的优化问题

\[\begin{align} &\min_x\quad f(x)\\\ &\begin{array}\\\ s.t.&g_i(x) \le 0,~i=1,\ldots,m\\\ &h_j(x)=0,~j=1,\ldots,r \end{array} \end{align}\]

其増广拉格朗日函数为

\[\begin{align} L(x,u,v) = f(x) + \sum_{i=1}^m u_ig_i(x) + \sum_{j=1}^r v_jh_j(x)~~(u_i \ge 0) \end{align}\]

则原问题的拉格朗日对偶函数为

\[\begin{align} g(u,v) = \min_x L(x,u,v) \end{align}\]

且原问题的对偶问题为

\[\begin{align} &\max_{u,v}\quad g(u,v)\\\ &\begin{array}\\\ s.t.&u_i \ge 0,~i=1,\ldots,m \end{array} \end{align}\]

上面得到对偶问题的简单推导流程如下：

首先原问题的目标函数加上约束可以表示为

\[\begin{align} f(x) = \max_{u,v} L(x,u,v) \end{align}\]

原因是在增广拉格朗日函数中，假如 \(x\) 违反了约束条件 (即 $ g (x) > 0 $ )，那么 \(f(x)\) 会趋向无穷大；而不违反约束条件时，\(u\) 必须取 0 才能使得目标最小。

进一步，原问题可以表示为 \[\min_x \max_{u,v} L(x,u,v) \]

而由于下式恒成立（弱对偶定理）

\[\begin{align} \min_x \max_{u,v} L(x,u,v) \ge \max_{u,v} \min_xL(x,u,v) \end{align}\]

因此将 \(\min_xL(x,u,v)\) 作为对偶函数， \(\max_{u,v} \min_xL(x,u,v)\) 作为对偶问题。

假设现在找到了对偶问题，并且对偶问题比原问题要容易求解得多，也求出了对偶问题的解，那么该转化去求原问题的解，这里就要用到下面的 KKT 条件。

KKT 条件

KKT 条件是非线性规划领域中最重要的理论成果之一，是确定某点是最优点的一阶必要条件，只要是最优点就一定满足这个条件，但是一般来说不是充分条件，因此满足这个点的不一定是最优点。但对于凸优化而言，KKT 条件是最优点的充要条件。

同样地

对于下面的优化问题

\[\begin{align} &\min_x\quad f(x)\\\ &\begin{array}\\\ s.t.&g_i(x) \le 0,~i=1,\ldots,m\\\ &h_j(x)=0,~j=1,\ldots,r \end{array} \end{align}\]

其増广拉格朗日函数为

\[\begin{align} L(x,u,v) = f(x) + \sum_{i=1}^m u_ig_i(x) + \sum_{j=1}^r v_jh_j(x)~~(u_i \ge 0) \end{align}\]

则 KKT 条件为

\[\begin{cases} \nabla_x L(x,u,v) = 0\\\ u_ig(x) = 0\\\ u_i \ge 0\\\ g_i(x) \le 0, h_j(x)=0 \end{cases}\]

因此其实只要能够求解出上面的联立方程组，得到的解就是最优解（对于凸优化而言，非凸的问题一般用 KKT 来验证最优解）。

但是上面的方程组往往很难求解，一些特殊情况下解是有限的，可以分类讨论；但是更一般的情况下可能的解是无限的，因此无法求解。这里要结合上面的拉格朗日对偶问题得到的解进行求解。

求解之前，首先要知道下面的定理 > 假如一个问题满足强对偶，那么 \(x',u',v'\) 是原问题和对偶问题的最优解 \(\longleftrightarrow\) \(x',u',v'\) 满足 KKT 条件。

因此通过对偶问题求得 \(u',v'\) 后，带入上面的 KKT 条件即可求出 \(x'\) 。

svm 是利用拉格朗日对偶和 KKT 条件进行求解的经典问题，这里不详细展开，有兴趣的可以参考 Andrew Ng 公开课中关于 svm 的那章或这篇文章。

ADMM

ADMM (Alternating Direction Method of Multipliers) 是解决带约束的凸优化问题的一种迭代解法，当初提出这个算法最主要的目的是为了在分布式环境 (Hadoop, MPI 等) 中迭代求解这个问题，关于这方面的资料可参考这里

ADMM 将要解决的问题描述成以下形式

\[\begin{align} &\min_x\quad f_1(x_1) + f_2(x_2)\\\ &\begin{array}\\\ s.t.& A_1x_1+A_2x_2 = b \end{array} \end{align}\]

这里省略证明过程，直接给出 ADMM 的迭代公式

\[\begin{align} &x_1^{(k)} = argmin_{x_1} f_1(x_1) + \frac{\rho}{2}||A_1x_1+A_2x_2^{(k-1)} - b + w^{(k-1)}||_2^2\\\ &x_2^{(k)} = argmin_{x_2} f_2(x_2) + \frac{\rho}{2}||A_1x_1^{(k)} + A_2x_2 - b + w^{(k-1)}||_2^2\\\ &w^{(k)} = w^{(k-1)} + A_1x_1^{(k)} + A_2x_2^{(k)} - b \end{align}\]

上式中的 \(\rho\) 是事先选择的参数，可以选择定值，选择定值的时候会遇到跟梯度下降固定步长的类似问题，因此也可以根据每次迭代情况改变 \(\rho\) 的值，具体可参考这篇文献。

实际中，难点在于把一个问题变为 ADMM 求解的形式，即上面列出的优化问题的形式。下面给出一个例子说明这个问题，这个例子是一个更一般的 lasso regression 问题，称为 fused lasso regression.

\[\begin{align} \min_{\beta \in \mathbb {R}^n} \frac{1}{2} ||y-X\beta||_2^2 + \lambda ||D\beta||_1~~(\lambda \ge 0) \end{align}\]

一般的 lasso regression 问题中 \(D = I\). 下面用 ADMM 的形式表示上面的问题

\[\begin{align}\min_{\beta \in \mathbb {R}^n，\alpha \in \mathbb {R}^n} \frac{1}{2} ||y-X\beta||_2^2 + \lambda ||\alpha||_1~~(\lambda \ge 0)\\\ s.t. D\beta - \alpha = 0\end{align}\]

将这个问题映射到上面的优化问题的模式有

\[\begin{align}\frac{1}{2} ||y-X\beta||_2^2\rightarrow f_1(x1) \\\ \lambda ||\alpha||_1 \rightarrow f_2(x_2)\\\ D\beta - \alpha = 0 \rightarrow A_1x_1+A_2x_2 = b\end{align}\]

则根据上面的迭代公式计算（对问题变量求导且令结果为 0）可得到下面的迭代公式

\[\begin{align} &\beta^{(k)} = (X^TX+\rho D^TD)^{-1}(X^Ty+\rho D^T(\alpha^{(k-1)}-w^{(k-1)})\\\ &\alpha^{(k)} = S_{\lambda/\rho}(D\beta^{(k)}+w^{(k-1)})\\\ &w^{(k)} = w^{(k-1)} + D\beta^{(k)} - \alpha^{(k)} \end{align}\]

而对于无约束的优化也可以通过 ADMM 求解，例如对于下面的问题

\[\begin{align} \min_x \sum_{i=1}^B f_i(x) \end{align}\]

将其表示为 ADMM 的形式如下

\[\begin{align}\min_{x_1,..x_B,x} \sum_{i=1}^B f_i(x_i)\\\ s.t. x_i = x,~~i=1,..B\end{align}\]

则 ADMM 的迭代规则如下

\[\begin{align} &x_i^{(k)} = argmin_{x_i} f_i(x_i)+\frac{\rho}{2}||x_i-x^{(k-1)}+w_i^{(k-1)}||~(i=1,..B)\\\ &x^{(k)} = \frac{1}{B} \sum_{i=1}^B (x_i^{(k)} + w_i^{(k-1)})\\\ &w_i^{(k)} = w_i^{(k-1)} + x_i^{(k)} - x^{(k)}~(i=1,..B) \end{align}\]