本文主要以LeetCode上的几道题目: 684.
Redundant Connection 、 685.
Redundant Connection II 和 721.
Accounts Merge 为例讲解并查集(merge–find
set )这种数据结构的应用。
说到并查集,不得不提的是最小生成树,因为并查集的最经典的应用地方便是解决最小生成树的
Kruskal 算法。
最小生成树
有两个经典的算法可用来解决 最小生成树
问题: Kruskal
算法 和 Prim
算法 。其中 Kruskal
算法中便应用了并查集这种数据结构,该算法的步骤如下
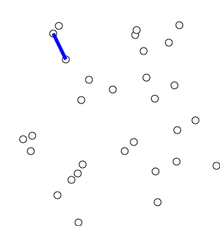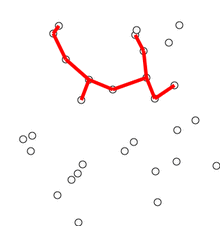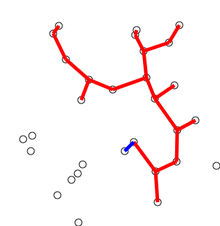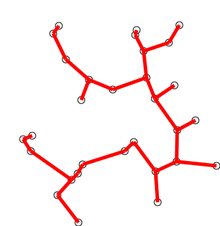
新建图G,G中拥有原图中相同的节点,但没有边
将原图中所有的边按权值从小到大排序
从权值最小的边开始,如果这条边连接的两个节点于图G中不在同一个连通分量中,则添加这条边到图G中
重复3,直至图G中所有的节点都在同一个连通分量中
该算法的动图显示如下(摘自维基百科)
KruskalDemo.gif-415.5kB
Kruskal 算法很简单,实际上 Kruskal
算法是一种贪心算法,并且已被证明最终能够收敛到最好结果。而在实现 Kruskal
算法时,则需要用到并查集这种数据结构来减小算法的时间复杂度。下面将详细介绍这种数据结构。
在介绍并查集前,顺便介绍一下 Prime 算法,Prime
算法也是一种贪心算法,而且也被证明了最终能够得到最好的结果,只是两者的侧重点不同,
Kruskal 算法维护的是一个边的集合,而 Prime
算法则同时维护了一个边的集合和一个点的集合,Prim 算法的过程如下
输入:一个加权连通图,其中顶点集合为V,边集合为E;
初始化:Vnew = {x},其中x为集合V中的任一节点(起始点),Enew =
{};
重复下列操作,直到Vnew = V:
在集合E中选取权值最小的边(u, v),其中u为集合 Vnew
中的元素 ,而v则是V中没有加入Vnew的顶点(如果存在有多条满足前述条件即具有相同权值的边,则可任意选取其中之一);
将v加入集合Vnew中,将(u, v)加入集合Enew中;
输出:使用集合Vnew和Enew来描述所得到的最小生成树。
其动图描述如下(摘自维基百科)
PrimAlgDemo.gif-51.1kB
并查集
在上面描述的 Kruskal 算法中,第三步是
从权值最小的边开始,如果这条边连接的两个节点于图G中不在同一个连通分量中,则添加这条边到图G中
而判断这条边连接的两个节点是否在同一个连通分量中,
实际上就是判断加入了这条边后,是否会与原来已经添加的边形成环路 ,并查集正是高效的实现了这个功能。
并查集主要有三种操作:MakeSet,Find 和 Union。
MakeSet 是初始化操作,即为每个 node
创建一个连通分量,且这个 node
为这个连通分量的代表,这里连通分量的代表指的是当连通分量中有多个点时,需要从这些点中选出一个点来代表这个连通分量,而这个点也往往被称为这个连通分量的
parent(意思即指这个点是其他点的 parent)Find 是指找到这个点所属的连通分量的 parentUnion
是指将两个连通分量合并成一个连通分量,并选出代表这个连通分量的新的
parent
那么怎么通过上面这几种操作判断某条边是否会与原来的边形成环路呢? 具体操作如下
给定一条边,为这条边的两个顶点执行 Find 操作,假如两个顶点的 parent
一样,那么说明这两个点已经在同一个连通分量中,再添加就会导致闭环
当两个点的 parent 不同,即两个点在不同的连通分量时,需要通过 Union
操作将这两个连通分量连起来
重复 1、2 步操作直到所有边遍历完
在具体实现,往往并不需要集合这种数据结构,而是仅仅通过数组即可,比如说有
n 个点,那么就创建一个长度为 n
的数组,每个下标代表一个点,而下标对应的值则代表这个点的 parent。
并查集还有两个重要的概念 path compression 和 union by
rank,目的均是降低时间复杂度,下面会详细说明。
现在通过具体的题目来讲解上面提到若干概念
Redundant Connection
684.
Redundant Connection
这道题目实际上就是要找到一个无向图中形成环路的最后那条边(输入保证了所有边会形成回路)。首先,看一种最简单的解决方法
1 2 3 4 5 6 7 8 9 10 11 12 class Solution : def findRedundantConnection (self, edges ): parents = range (1001 ) for edge in edges: v1, v2 = edge[0 ], edge[1 ] if parents[v1] == parents[v2]: return edge tmp = parents[v2] for i in xrange(len (parents)): if parents[i] == tmp: parents[i] = parents[v1] return None
这种方法中每次 Find 的时间复杂度为 \(O(1)\) (即 parents[v1] 操作), 每次 Union
则需要遍历所有的点,时间复杂度是 \(O(n)\) ,总体时间复杂度是 \(O(mn)\) , \(m\) 为边的数目,而 \(n\) 为点的数目。
而我们也可以改变思路,就是进行 Union
操作时不再将某个连通分量中所有点的 parent 改为另一个连通分量的
parent,而是只改变那个连通分量的代表;这样进行 Find
操作的时候只需要递归的查找即可,下面为这种思路对应的代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 class UnionFindSet (object ): def __init__ (self ): self.parents = range (1001 ) def find (self, val ): if self.parents[val] != val: return self.find(self.parents[val]) else : return self.parents[val] def union (self, v1, v2 ): p1, p2 = self.find(v1), self.find(v2) if p1 == p2: return True else : self.parents[p1] = p2 return False class Solution (object ): def findRedundantConnection (self, edges ): """ :type edges: List[List[int]] :rtype: List[int] """ ufs = UnionFindSet() for edge in edges: if ufs.union(edge[0 ], edge[1 ]): return edge
这个方法每次 Union 的时间复杂度为 \(O(1)\) , 但是每次 Find 的时间复杂度是 \(O(n)\) ,所以总体时间复杂度还是 \(O(mn)\) ,
那么有没有一种改进总体时间复杂度的方法呢?
答案就是上面提到的 path compression 和 union by rank。
path compression 指的是在上面的递归的 Find
操作中,将最终得到的结果赋给递归过程中经过的所有点,从而降低连通分量的高度,实际上可以将一个连通分量当做一颗树,树的每个节点都连着其
parent ,而 path compression
则相当于将搜寻路径中的所有点直接连到最终的那个 parent
上,因此能够降低树的高度。
降低树的高度有什么好处?那就是能够降低查找的时间复杂度,从 \(O(n)\) 降为了 \(O(logn)\) ,
因为原来的递归搜索实际上是在一颗每个节点只有一个子节点的树上进行搜索,树的高度即为点的个数,而通过
path compression 则能够有效降低树的高度。
另外一个问题就是进行 Union
操作时,需要将高度低的树连接到高度较高的树上,目的是为了减少 Union
后的整棵树的高度,这就是 union by rank, rank 代表的就是树的高度。
采用 path compression 和 union by rank 后,Find 的时间复杂度变为了
\(O(logn)\) , Union 的时间复杂度为 \(O(1)\) , 因此总体时间复杂度是 \(O(mlogn)\) , \(m\) 为边的数目,而 \(n\) 为点的数目。改进后的代码如下
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 class UnionFindSet (object ): def __init__ (self ): self.parents = range (1001 ) self.rank = [0 ] * 1001 def find (self, val ): """find with path compression""" if self.parents[val] != val: self.parents[val] = self.find(self.parents[val]) return self.parents[val] def union (self, v1, v2 ): """union by rank, check whether union two vertics will lead to a cycle""" p1, p2 = self.find(v1), self.find(v2) if p1 == p2: return True elif self.rank[p1] > self.rank[p2]: self.parents[p2] = p1 elif self.rank[p1] < self.rank[p2]: self.parents[p1] = p2 else : self.rank[p2] += 1 self.parents[p1] = p2 return False class Solution (object ): def findRedundantConnection (self, edges ): """ :type edges: List[List[int]] :rtype: List[int] """ ufs = UnionFindSet() for edge in edges: if ufs.union(edge[0 ], edge[1 ]): return edge
Redundant Connection II
685.
Redundant Connection II
从前面的无向图升级到了有向图,对应的要求从原来的仅要求不形成环路升级到在不形成环路的基础上,拓扑必须要是一棵合法树,也就是每个点只能有一个父节点,例如
[[2,1],[3,1]] 这两条边虽然没有形成环路,但是 1
有两个父亲节点(2和3),因此不是一棵合法的树。
由于题目说明了输入只有一条不合法的边,因此首先可以统计一下这些边中是否存在某个点有两个父亲节点,假如有,则需要移除的边必定为连着这个点的两条边中的一条 ,通过上面
Union-find
的方法,可以判断出假如移除掉连着这个点的第一条边时,是否会形成回路。如果会,则说明需要移除第二条边,否则直接移除第一条边。
如果统计的结果中没有点含有两个父亲节点,那么可以直接通过第一题的方法直接找到形成回路的最后那条边。AC的代码如下
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 class UnionFindSet (object ): def __init__ (self ): self.parents = range (1001 ) self.rank = [0 ] * 1001 def find (self, val ): """find with path compression""" if self.parents[val] != val: self.parents[val] = self.find(self.parents[val]) return self.parents[val] def union (self, v1, v2 ): """union by rank, check whether union two vertics will lead to a cycle""" p1, p2 = self.find(v1), self.find(v2) if p1 == p2: return True elif self.rank[p1] > self.rank[p2]: self.parents[p2] = p1 elif self.rank[p1] < self.rank[p2]: self.parents[p1] = p2 else : self.rank[p2] += 1 self.parents[p1] = p2 return False class Solution (object ): def findRedundantDirectedConnection (self, edges ): """ :type edges: List[List[int]] :rtype: List[int] """ redundant_edges = None count = {} for e in edges: if e[1 ] not in count: count[e[1 ]] = [] count[e[1 ]].append(e) if len (count[e[1 ]]) == 2 : redundant_edges = count[e[1 ]] break if redundant_edges: ufs = UnionFindSet() for edge in edges: if edge == redundant_edges[1 ]: continue if ufs.union(edge[0 ], edge[1 ]): return redundant_edges[0 ] return redundant_edges[1 ] else : ufs = UnionFindSet() for edge in edges: if ufs.union(edge[0 ], edge[1 ]): return edge
Accounts Merge
这道题目虽然也用到了并查集的数据结构,但是与前面的两道题目又有点不同,主要体现在两个方面
节点不再以数字标识,因此标识 parents 的数据结构要从 array 变为
map
不需要判断是否形成闭环,而要返回最终各个集合内的元素;在这个操作中需要注意的是不能直接利用存储各个节点的
parent 的 map 直接为每个节点找到其 parent, 因为并非各个节点都进行了
path compression。对应有两种方法 (1)借助 find 方法找到各个节点的parent
(2) 对存储各个节点的 parent 的 map 再进行一次 path compression,
然后直接在 map 中找到各个节点的 parent 对应的方法入下
方法(1)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 class Solution (object ): def accountsMerge (self, accounts ): """ :type accounts: List[List[str]] :rtype: List[List[str]] """ owners, parents = {}, {} for account in accounts: owners[account[1 ]] = account[0 ] for i in xrange(1 , len (account)): parents[account[i]] = account[i] for account in accounts: p = self.find(account[1 ], parents) for i in xrange(1 , len (account)): parents[self.find(account[i], parents)] = p unions = {} for account in accounts: for i in xrange(1 , len (account)): p = self.find(account[i], parents) unions.setdefault(p, set ()) unions[p].add(account[i]) result = [] for k, v in unions.items(): result.append([owners[k]] + sorted (v)) return result def find (self, email, parents ): if parents[email] != email: parents[email] = self.find(parents[email], parents) return parents[email]
方法(2)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 class Solution (object ): def accountsMerge (self, accounts ): """ :type accounts: List[List[str]] :rtype: List[List[str]] """ owners, parents = {}, {} for account in accounts: owners[account[1 ]] = account[0 ] for i in xrange(1 , len (account)): parents[account[i]] = account[i] for account in accounts: p = self.find(account[1 ], parents) for i in xrange(1 , len (account)): parents[self.find(account[i], parents)] = p for k, v in parents.items(): if k!=v: parents[k] = self.find(parents[v], parents) unions = {} for k, v in parents.items(): if v not in unions: unions[v] = set () unions[v].add(k) result = [] for k, v in unions.items(): result.append([owners[k]] + sorted (v)) return result def find (self, email, parents ): if parents[email] != email: parents[email] = self.find(parents[email], parents) return parents[email]