《Forecasting High-Dimensional Data》阅读笔记

发表于 2018-11-15 标签计算广告，机器学习

《Forecasting High-Dimensional Data》是 Yahoo! 一篇关于流量预估的论文。在合约广告中，需要提前预估某个定向下的流量情况，从而进行合理的售卖和分配。但是由于定向的组合非常多（广告主的多样的需求导致的），而工程上不允许为每个可能的定向预估其流量，因此这篇论文提出了先预估一些基本定向的流量，然后通过 correlation model 从基本定向的流量计算出各种定向下的流量情况，具有较强的工程性，也是之前提到的文章《Budget Pacing for Targeted Online Advertisements at LinkedIn》中采用的流量预估方法。

问题定义

前面简单提到了文章解决的问题的背景，文章将一个最基本的定向（如性别为男）称为一个 attribute，而每个广告主的需要的流量就是若干个 attribute 的 combination，因此 combination 的数量是非常庞大的，文章要求的就是如何有效地预估所有 combination 的流量情况。

一个最直观的思路就是统计出某个 combination 的历史数据，然后训练模型并进行预估。但是这个方法最致命的地方在于统计 combination 的历史数据以及模型训练所需的耗时在实际中是无法容忍的，需要数小时（文章要求需要在数百毫秒内返回某个 combination 的流量预估值）。那可以将这些放到离线来做么？答案也是不可以的，因为我们不知道哪些 combination 在未来会用到，因此所有的 combination 都需要进行预估，而这个数量过于庞大了。

解决思路

文章提出的解决思路是先对一小部分有代表性的 combination 进行上面的历史统计和预估操作，这里的有代表性的流量可以从统计的历史数据中得到（如访问量最多的 combination 等），也可以手工选择等；然后结合文章提到的 correlation model，可以从这一小部分的 combination 中预估出所有的 combination 的流量情况。

下面具体详细介绍整体的解决思路

系统总览

文章提出的方法系统图如下，每个的 Historical Data Point 实际上就是一个历史 query，包含了某些 attribute 的组合，这些数据主要有两个用途

（1）送入到 Historical Data Aggregator 中对某些有代表性的 Selected Attribute Combinations 进行历史统计，并通过模型进行时间序列的预估，这里的时间序列预估使用了 SARIMA 模型（2）用于构建 Correlation Model，并与上面若干 Selected Attribute Combinations 的预估结果共同对在线的 query 返回预估值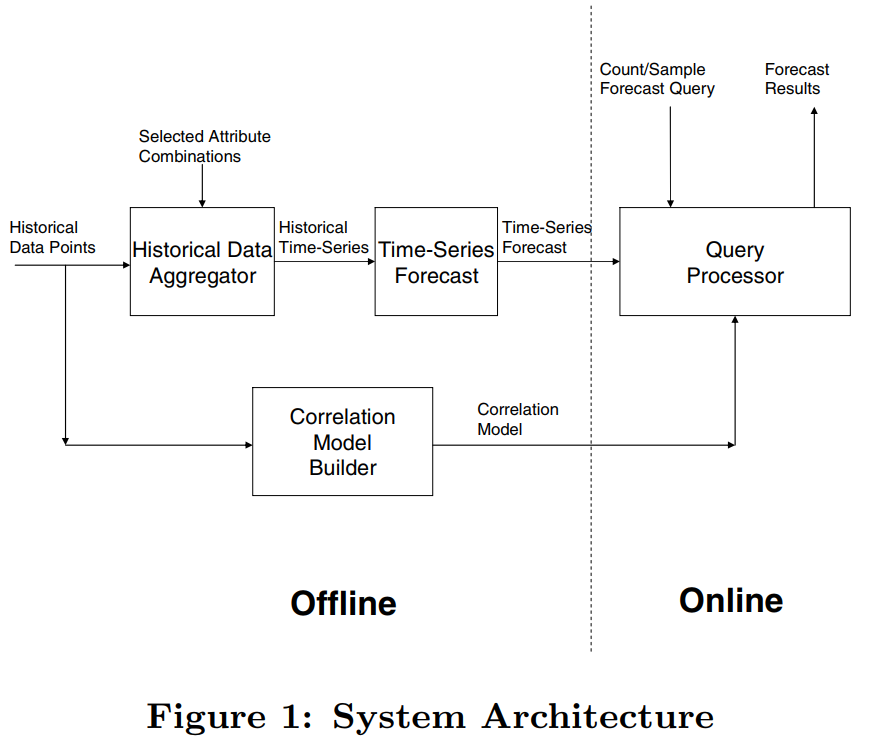

可以看到文章的重点在于 correlation model 的构建以及 correlation model 在 online 部分是如何工作的。

Correlation Model

上文提到了对一部分有代表性的 combination（也就是上图中的 Selected Attribute Combinations）进行时间序列预估，这里记为 \(Q = \lbrace Q_1, Q_2,... Q_m \rbrace\), 称其为 base queries。则对于一个在线的 query \(q\), 其预估步骤如下

选择 \(Q\) 中某个 base query \(Q_k\), 使得 \(q \subseteq Q_k\)
计算 \(Q_k\) 在未来时间 \(T\) 内的流量，记为 \(B(Q_k, T)\)
计算 \(q\) 在 \(Q_k\) 中出现的概率，记为 \(R(q|Q_k)\)
返回 \(q\) 的预估结果为 \(B(Q_k, T) \times R(q|Q_k)\)

Correlation Model 所做的事情就是第 3 步：计算比例。

而在第一步中，必然会存在某个 \(Q_k\)，使得 \(q \subseteq Q_k\) , 为什么呢？

假设总共有 n 个 attribute，那么只要将每个 attribute 作为一个 base query（这样 \(Q\) 中便有了 n 个 base queries），则 attribute 的任意 combination 肯定会属于 Q 中的某几个 base queries 的。那如果不止一个 \(Q_k\)，使得 \(q \subseteq Q_k\) 时该怎么办？这时候就需要选择一个最小的 \(Q_k\), 这里的最小指的是不存在某个 \(Q_l\) 同时满足 \(q \subseteq Q_l\) 且 \(Q_l \subseteq Q_k\)。举个简单的例子，假如有两个 base queries \(Q1 = a_1 , Q_2 = a1 \wedge a_2\), 则对于某个 query \(q = a1 \wedge a_2 \wedge a_3\)，应该选择 \(Q_2\) 作为 \(Q_k\)。

下面分别讲述文中提到的三种 correlation model

Full Independence Model (FIM)

FIM 实际上就是个 Naive Bayes，假设了每个 attribute 是相互独立的，也就是

\[\begin{align} R(Gender = male \wedge Age < 30|Q_k) = R(Gender = male|Q_k) \times R(Age < 30|Q_k) \end{align}\]

也就是只要为 \(Q_k\) 每个单独的 attribute 计算其比例 \(R(.| Q_k)\) 即可。具体计算方法如下

\[\begin{align} R(a_i|Q_k) = \frac{|a_i \in (Q_k \wedge P_t)|}{|Q_k \wedge P_t|} \end{align}\]

Partwise Independence Model (PIM)

将所有的 attribute 都认为是相互独立的显然是不合理的，因为有某些 attribute 之间是相互关联的，比如说年龄和收入一般是存在关联的，因为 PIM 实际上就是将某些可能有关联的 attribute 的比例一起计算。即

\[R(Gender = male \wedge Age < 30 \wedge Incom > 10000|Q_k) = R(Gender = male|Q_k) \times R(Age < 30 \wedge Incom > 10000|Q_k)\], 而比例的计算公式也跟上面的类似

Sampling-based Joint Model(SJM)

上面的两种方法均假设了 attribute 之间的的相互独立性，这依然会存在一定的局限性，能够完全避免独立性的假设呢？这篇文章提出的 Sampling-based Joint Model (SJM) 就避免了独立性的假设。

虽然说是 model ，但是方法还是统计，只是为了避免数量太大，首先做了 sampling，选出经过 sample 后的数据并记为 \(S\)，然后计算 base query \(|Q_k|\) 在 \(S\) 中的数量 \(|Q_k \cap S|\), 这部分会在离线做，然后在线来了一个 query \(q\) 后，会计算在 \(S\) 中满足 \(q\) 的数量并记为 \(n\)。则比例计算公式就很简单了

\[\begin{align} R(q|Q_k) = \frac{n}{|Q_k \cap S|} \end{align}\]

整个过程思路非常简单，没有涉及到 attribute，因此也没有 attribute independent 的假设。但是关键的问题在于如何高效地算出上面的分子和分母的那些计数。论文使用的是 bitmap index, 且使用了论文 Optimizing bitmap indices with efficient compression 中提出的关于 bitmap index 的一种改进方法。

实验效果

数据

实验采用的数据是 Yahoo！部分页面过去一年的历史访问数据，其中一半用于进行 time-series forecasting，另一半用于验证效果（按时间划分），且对于某些 combination 用了过去四年累积的数据进行 forecasting。Correlation Model 则用了过去一周的数据进行训练，且 SJM 采样得到了 20 million 的数据。

评估指标

工程上的评估指标有 speed 和 space，就是时间和空间的评估。

效果上的评估指标主要就是 accuracy，采用的是 absolute percentage error (APE), 假设预估值为 \(F\), 真实值为 \(A\), 则 APE 的定义如下

\[\begin{align} APE = \frac{|F-A|}{A} \end{align}\]

APE 针对的是单个 query，但是往往希望的是验证一系列 query 的效果，其指标为 Root Mean Square Error (RMSE)，定义如下，\(w_q\) 表示每个 query 的权重，这个值被设为 query 在过去两年的合约中出现的次数

\[\begin{align} RMSE = \sqrt{\frac{\sum_{q \in Q}w_qAPE^2(q)}{\sum_{q \in Q}w_q}} \end{align}\]

效果对比

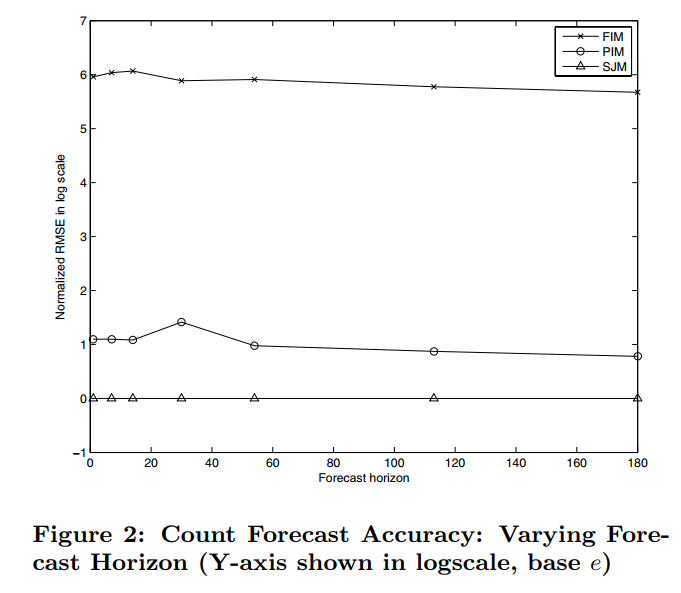
下面是三个模型的 RMSE（取了对数）效果对比，横轴的 forecast horizon 表示预估未来多少天的时的效果。可以看到假设 attribute independent 会降低最后的效果。

除此之外，每个模型在进行 online 是返回结果的耗时都要小于 50 毫秒；且 FIM 和 PIM 模型的内存占比大概是 500 MB，因为这两个模型只需要存储比例值和预估的趋势曲线，但是 SJM 的内存大概到了 20GB（20 million 的 data points），空间主要由 bit-map index 消耗。