EE 问题概述

发表于 2019-01-05 标签计算广告，机器学习

EE (Exploitation & Exploration) 问题在计算广告 / 推荐系统中非常常见，甚至在更广义的范围上，任意决策问题都会牵涉到 EE 问题。简单来说，这个问题就是要解决的是在决策时到底是根据已有经验选择最优的策略 (Exploitation)，还是去探索一些新的策略来提升未来的收益 (Exploration)。本文主要介绍解决这个问题的三种比较常见的方法：随机方法，UCB 方法，Thompson sampling 方法，侧重于方法的具体流程和基本思想。

MAB 建模

EE 问题一般会通过 MAB (Multi-Armed Bandit) 进行建模，如下所示，所有 arm 就是每次决策中可作出的选择，拉下某个 arm 表示作出了相应的选择。

MAB 符号化表述如下

MAB 可表示为一个二元组 <$A, R$>
$A$ 表示为一系列可能的动作，$R(r|a)$ 则表示给定动作下的奖赏的分布，
每一时刻根据给定策略从 $A$ 选择动作 $a_t$, 同时环境根据分布 $R(r|a)$ 生成奖赏 $r_t$
目标是最大化奖赏之和 $\sum_{t=1}^T r_t$

上面的第 3 步的策略就是下面要介绍的 EE 问题的解决方法，除去随机方法，UCB 方法和 Thompson sampling 方法的思想均是通过定义每个 arm 的收益的期望，然后选择收益期望最大的 arm。UCB 是频率学派的思想，认为每个 arm 的收益期望是固定的，通过试验记录得到其历史收益状况，然后加上一个 bound 构成了收益期望；Thompson sampling 则是贝叶斯学派的思想，认为 arm 的收益期望服从一个特定的概率分布，通过试验记录更新分布的参数，然后从每个 arm 的分布中产生收益期望。

而根据一个 arm 的历史试验记录判断其优劣又有两种方法，因而也衍生了两类 bandit 问题：Bernoulli Bandit 和 Contextual Bandit。在 Bernoulli Bandit 中，认为每个 arm 的优劣（即当前试验是否产生收益）是服从伯努利分布的，而分布的参数可以通过历史收益状况求解；而在 Contextual Bandit 中，没有直接定义出一个概率分布来描述每个 arm 的优劣，而是假设了 arm 的优劣和描述 arm 的特征组成的向量 $x$ 存在一个线性关系：$x^T \theta$，参数 $\theta$ 可通过历史样本求解和更新。

UCB 方法和 Thompson sampling 方法均可解决这两类问题，UCB 解决 Bernoulli Bandit 的方法有 UCB1，UCB2 等，解决 Contextual Bandit 的方法有 LinUCB 等；而 Thomson Sampling 解决 Bernoulli Bandit 时采用了 Bernoulli 分布和 Beta 分布，解决 Contextual Bandit 时采用了两个正态分布。后面会详细介绍这些方法。

随机方法

$\epsilon$-greedy

$\epsilon$-greedy 是一种最简单的随机方法，原理很简单：每次决策时，以 1 - $\epsilon$ 的概率选择最优的策略，以 $\epsilon$ 的概率随机选择任意一个策略；并且在每次做出决策获取到真实的 reward 后更新每个决策的收益情况（用于选择最优策略）。伪代码实现可参考 Multi-Armed Bandit: epsilon-greedy

$\epsilon$-greedy 存在着以下几个比较显著的问题

$\epsilon$ 是个超参数，设置过大会导致决策随机性过大，设置过小则会导致探索性不足
$\epsilon$-greedy 策略运行一段时间后，对各个 arm 的收益情况有所了解，但没有利用这些信息，仍然不做任何区分地随机 exploration（会选择到明显较差的 item）
$\epsilon$-greedy 策略运行一段时间后，但仍然花费固定的精力去 exploration，浪费了本应该更多进行 exploitation 机会

针对第 2 个问题，可以在 $\epsilon$-greedy 策略运行一段时间后，选择出收益最高的前 $n$ 个 arm，然后 exploration 时从这 $n$ 个 arm 中随机选择。

针对第 3 个问题，可以设置进行 exploration 的概率 $\epsilon$ 随着策略进行的次数而逐渐下降，比如说可以取如下的对数形式，$m$ 表示目前进行了 $m$ 次的决策

\[\begin{align} \epsilon = \frac{1}{1 + \log(m+1)} \end{align}\]

Softmax

通过 Softmax 进行的 Exploration 也称为 Boltzmann Exploration，这个方法通过一个温度参数来控制 exploration 和 exploitation 的比例，假设各个 arm 的历史收益为 $\mu_0$, $\mu_1$, ......, $\mu_n$, 温度参数记为 $T$，则选择某个 arm 时参考的指标为

\[\begin{align} p_i = \frac{e^{\mu_i/T}}{\sum_{j=0}^{n} e^{\mu_j/T}}(i=0, 1,...., n) \end{align}\]

当温度参数 $T=1$, 上面的方法就是纯粹的 exploitation；而当 $T \to \infty$ 时，上面的方法就是纯粹的 exploration，因此，可以控制 $T$ 的范围来控制 exploration 和 exploitation 的比例。某些文献也会将 $1/T$ 称为学习率。一个很直观的想法就是让 $T$ 随着策略运行次数的增加而下降，这样便可让策略从偏向 exploration 转为偏向 exploitation。

但是，这篇 paper Boltzmann Exploration Done Right 证明了单调的学习率（即 $1/T$）会导致收敛到局部最优，并提出了一种针对不同的 arm 采用不同的学习率的方法，但是形式已经不是上面的 softmax 形式了。文章涉及的证明和公式符号较多，这里不再展开阐述，感兴趣读者可自行参考。

UCB 方法

假如能够对每个 arm 都进行足够多次的试验，根据大数定律，次数越多，这些试验结果统计得到的收益便会约接近各个 arm 真实的收益。然而在实际中，只能对各个 arm 进行有限次的试验，因此这会导致根据统计得到的收益跟真实的收益存在一个误差，UCB 的核心就在于如果预估这个误差 (也就是 UCB 中的 B (bound))，然后将 arm 统计的收益加上其通过 UCB 方法计算出来的 bound 进行排序，选择最高的那个。

UCB1

UCB1 方法的理论基础是 Hoeffding's inequality，该不等式的定义如下

假设 $X_1, X_2...X_n$ 是同一个分布产生的 $n$ 个独立变量，其均值为 $\overline{X} = \frac{1}{n}\sum_{i=1}^n X_i$, 则如下公式成立 \[\begin{align} p(|E[X] - \overline{X}| \le \delta) \ge 1 - 2e^{-2n\delta^2} \end{align}\]$$

更直观地说，该不等式表明了 $n$ 个独立同分布的变量的均值与该变量的真实期望的误差小于某个预设的阈值 $u$ 会以概率 $1 - e^{-2nu^2}$ 恒成立。

回到我们的问题，可以将 $X_1, X_2...X_n$ 看做某个 arm 在 $n$ 次试验中获得的收益，则通过上面的式子可以设定一个 $\delta$ 使得公式成立，然后用 $\overline{X} + \delta$ 来近似真实的收益 $E(X)$；理论上也可用 $\overline{X} - \delta$，但是 UCB 方法会用上界，这也是 UCB 中 U (upper) 的含义。那么现在的问题便是 $\delta$ 该选多大了？

UCB1 方法中将 $\delta$ 设为如下公式，公式中的 $N$ 表示目前所有 arm 试验的总次数，$n$ 表示某个 arm 的实验次数

\[\begin{align} \delta = \sqrt{\frac{2\ln{N}}{n}} \end{align}\]

直观地看上面定义的 $\delta$, 分子的 $N$ 对所有的 arm 是相同的，分母的 $n$ 则表示某个 arm 目前为止试验的次数，如果这个值越小，那么 $\delta$ 便越大，相当于 exploration；而当各个 arm 的 $n$ 相同时，实际上就是在比较各个 arm 的历史收益情况了。

UCB1 方法的流程如下，该图摘自 Optimism in the Face of Uncertainty: the UCB1 Algorithm

可以看到 UCB1 的 bound 完全是由 Hoeffding's inequality 推导出来的，而除了 Hoeffding's inequality，其他的一些 inequality 也能够推导出相应的 bound，Reinforcement Learning: Exploration vs Exploitation 中就提到了一些其他的 inequality

Bernstein’s inequality
Empirical Bernstein’s inequality
Chernoff inequality
Azuma’s inequality
.......

UCB2

从名字上基本就可以猜出 UCB2 是 UCB1 的改进，改进的地方是降低了 UCB1 的 regret 的上界，regret 指的是每次能获得的最大的收益与实际获得的收益的差距，这部分涉及到较多的数学证明，这里略去这部分，详细可参考 Finite-time Analysis of the Multiarmed Bandit Problem。UCB2 算法的流程如下，图片同样摘自 Finite-time Analysis of the Multiarmed Bandit Problem

从流程图上可知，UCB2 与 UCB1 相似，也是为每个 arm 计算一个 bound，然后根据 arm 的历史收益和 bound 选出 arm ，只是对这个 arm 不止试验一次，而是试验 $\tau(r_j+1) - \tau(r_j)$ 次。上面的 $a_{n, r_j}$ 和 $\tau(r)$ 定义如下，由于 $\tau(r)$ 要为整数，因此取了上界

\[\begin{align} a_{n,r} = \sqrt{\frac{(1+\alpha)\ln(ne/\tau(r))}{2\tau(r)}} \end{align}\]

\[\begin{align} \tau(r) = \lceil (1+\alpha)^r\rceil \end{align}\]

上面式子中的 $\alpha$ 是个超参数，根据上面给出的论文中的实验结果 (如下图所示)，这个值不能取得太大，论文建议值是 0.0001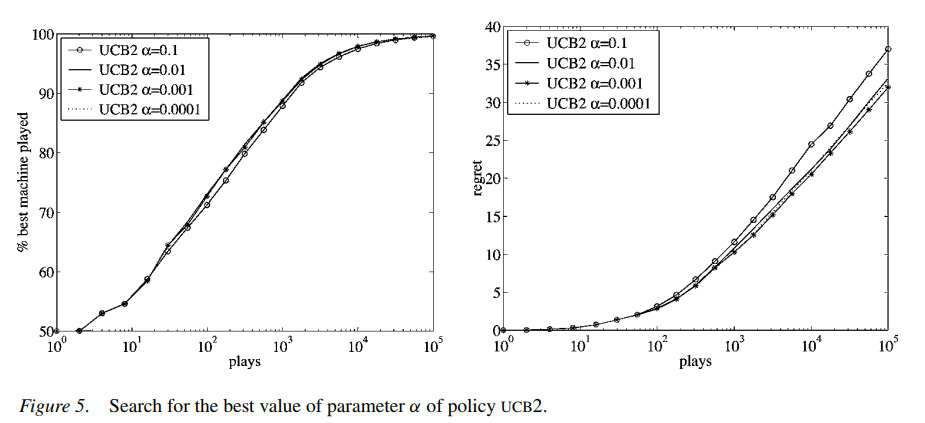

LinUCB

上面的 UCB1 和 UCB2 算法都是解决 Bernoulli Bandit 问题的，也就是假设每个 arm 的优劣是服从伯努利分布，而根据历史记录计算出的 $\overline {x}_j$（获得收益的试验次数和总试验次数的比值）其实就是伯努利分布的参数。

这样基于统计的方法很简单，但是问题也比较显著，因为 arm 的收益会跟多个因素有关（比如说某个 arm 在早上选择时没有收益，但是晚上就有了），利用这些信息可以预估得更准确；而基于统计的方法则忽略了这一点。

区别于 Bernoulli Bandit，这类利用了上下文信息的问题就是上面提到的 Contextual Bandit 问题，而 LinUCB 就是要解决这个问题的。 LinUCB 中没有直接定义出一个概率分布来描述每个 arm 的历史收益状况，而是假设了 arm 的优劣和描述 arm 的特征的向量 $x$ 存在一个线性关系： $x^T \theta$

实际上这是一个经典的 Linear Regression (收益不在局限于 0 和 1) 问题，$x$ 是 arm 的特征组成的向量 (需要根据具体的问题选择特征), $\theta$ 则是模型的参数，每一次的试验就是一条样本，label 为具体的收益。

通过历史样本可以求解出 $\theta$, 则在每次选择选择 arm 时，LinUCB 会用 $x^T \theta$ 来替换掉 UCB1 或 UCB2 中的 $\overline {x}_j$，但是这还不是 LinUCB 的全部，作为 UCB 类方法，LinUCB 中还是有个 bound 的，因为毕竟从历史记录只能对 arm 进行有限次的试验，预估出来的收益情况与真实的还是存在差距的。

UCB1 中推到出 bound 的 Hoeffding's inequality 不能直接应用到 LinUCB 中，而关于 linear regression 的 bound 最早是在这篇论文 Exploring compact reinforcement-learning representations with linear regression 中提出的，这里不详细展开具体的证明过程了。提出 LinUCB 的论文 A Contextual-Bandit Approach to Personalized News Article Recommendation 直接采用了这一结论，其表达形式，如下所示

\[\begin{align} p(|x_j^T\theta_j - E(r|x_j)| \le \alpha \sqrt{x_j^T(D_j^TD_j+I)^{-1}x_j}) \ge 1- \delta \end{align}\]

即对于某个 arm $j$, 计算出来的 $x_j^T\theta_j$ 与实际的期望相差小于 $ $ 的概率要大于 $1- \delta$, 其中 $D_j$ 是 arm $j$ 前面每次被观察到的特征组成的矩阵，比如说 arm $j$ 前面被观察了 $m$ 次，且特征组合成的向量的维度为 $d$, 则 $D_j$ 的大小为 $m$ X $d$, $I$ 为单位向量，而 $\alpha = 1 + \sqrt{\ln(2/\delta)/2}$ , 因此，只要根据概率选定 $\delta$，则各个 arm 的 bound 便可通过 $\alpha \sqrt{x_j^T(D_j^TD_j+I)^{-1}x_j}$ 求出。

因此 LinUCB 算法流程如下，算法同时包含了选择 arm 的方式和更新 linear regress 模型。

上面的每个 arm 的 linear model 的参数都是独立的，论文针对这对点设计了这些 model 共享的一些参数，即将原来某个 arm $j$ 计算出来的 $x_j^T\theta_j$ 换成了 $x_j^T\theta_j + z_j^T \beta$, $\beta$ 是各个模型共享的的参数，$z_j^T$ 则是这些参数对应的特征。对应这种情况，也有了论文的第二种算法

Thompson sampling 方法

前面的 UCB 方法采用的都是频率学派的思想，即认为评判某个 arm 的优劣的指标是个定值，如果有无限次的试验，便可准确地计算出这个值，但是由于现实中只能进行有限次的试验，因此预估出来的值是有偏差的，需要通过另外计算一个 bound 来衡量这个误差。

而下面要介绍的 Thompson sampling 方法采用的则是贝叶斯学派的思想，即认为评判某个 arm 的优劣的指标不再是个定值，而是服从着某种假定的分布 (先验)，通过观察到的历史记录去更新这个分布的参数 (似然)，得到了新的分布参数 (后验), 然后不断重复这个过程。当需要进行比较时，从分布中随机产生一个样本即可。

Bernoulli Bandit

前面提到，Bernoulli Bandit 假设某个 arm 的优劣服从伯努利分布，即每次是否获得收益的服从参数为 $\theta$ 的伯努利分布

$p(reward | ) Bernoulli() $

UCB 方法中的 UCB1 和 UCB2 都是通过简单的历史统计得到 $\overline {x}_j$ 来表示 $\theta$ 的，但是贝叶斯学派则认为 $\theta$ 服从着一个特定的分布，根据贝叶斯公式有

\[\begin{align} p(\theta|reward) = \frac{p(reward|\theta) p{(\theta)}}{p(reward)} \propto p(reward|\theta) p{(\theta)} ＝Bernoulli(\theta) p(\theta) \end{align}\]

$p(\theta|reward)$ 表示根据观察到的实验收益情况更新的后验概率，且由于似然 $p(reward|\theta)$ 为伯努利分布，为了保持共轭便于计算；先验分布 $p(\theta)$ 选择为了 Beta 分布，即 $Beta(\alpha, \beta)$，而两个分布相乘 $Bernoulli(\theta)*Beta(\alpha, \beta)$ 会得到一个新的 Beta 分布，简单来说，就是

当 $Bernoulli(\theta)$ 的结果为 1，则会得到 $Beta(\alpha + 1, \beta)$
当 $Bernoulli(\theta)$ 的结果为 0，则会得到 $Beta(\alpha, \beta + 1)$

因此，Bernoulli Bandit 中的 Thompson Sampling 步骤如下，图片摘自 A Tutorial on Thompson Sampling

Contextual Bandit

在 Bernoulli Bandit 中，我们假设 arm 是否获得收益是服从伯努利分布的，即 $p(reward | \theta) \sim Bernoulli(\theta)$

而在 Contextual Bandit 中，我们假设获得的收益和特征向量存在一个线性关系，即 $reward = x^T $，因此无法像前面一样直接通过似然 $p(reward | \theta) \sim Bernoulli(\theta)$ 来更新 $\theta$

但是根据前面解决 Bernoulli Bandit 的思路，只要定义 $p(reward|\theta)$ 和 $p(\theta)$ 为合适的共轭分布，那么就可以使用 Thompson Sampling 来解决 Contextual Bandit, 因为根据贝叶斯公式有如下的公式

\[\begin{align} p(\theta|reward) \propto p(reward|\theta) p{(\theta)} \end{align}\]

理论上，只要 $p(reward|\theta)$ 和 $p(\theta)$ 为共轭即可，但是考虑到假设的分布的合理性，参考这篇论文 Thompson Sampling for Contextual Bandits with Linear Payoffs，分别对这两个分布都采用正态分布的形式，论文给出了较多的数学证明，这里略去证明，直接给出最终结论

对于 $p(reward|\theta)$ ，由于估计 reward 为 $x^T\theta$ ，因此假设真实的 reward 服从以 $x^T\theta$ 为中心、 $v^2$ 为标准差的正态分布，即 $p(reward|\theta) \sim \mathcal{N}(x^T\theta, v^2)$, $v$ 的具体含义后面会给出

为了运算上的便利性， $p(\theta)$ 一般会选择与 $p(reward|\theta)$ 共轭的形式；由于 $p(reward|\theta)$ 是正态分布，那么 $p(\theta)$ 也应该是正态分布（正态分布的共轭还是正态分布）

为了便于给出后验概率的形式，论文首先定义了如下的等式

\[\begin{align} B(t) = I_d + X^TX \end{align}\]

\[\begin{align} \mu(t) = B(t)^{-1}(\sum_{\tau = 1}^{t-1} x_{\tau}^Tr_{\tau}) \end{align}\]

上面的 $t$ 表示某个 arm 第 $t$ 次的试验，$d$ 表示特征的维度，$X$ 的含义与 LinUCB 中介绍的一致，即是这个 arm 前 $t-1$ 次的特征组成的矩阵，在这个例子中其维度大小为 ($t-1$) X $d$, $r_{\tau}$ 则表示前面 $t-1$ 次试验中第 $\tau$ 次获得的 reward。

则 $p(\theta)$ 在 $t$ 时刻服从正态分布 $\mathcal{N}(\mu(t), v^2B(t)^{-1})$, 而 $p(\theta)$ 与 $p(reward|\theta)$ 相乘计算出来的后验概率 $p(\theta|reward) \sim \mathcal{N}(\mu(t+1), v^2B(t+1)^{-1})$

前面提到的 $v$ 的定义为 $v = R\sqrt{9d\ln(\frac{t}{\delta})}$，该式子中的 $t$ 和 $d$ 的含义与上面的相同，而 $R$ 和 $\delta$ 是需要自定义的两个常数，均是用在两个不等式中约束 regret bound 的，其中 $R \ge 0$ ,$0 \le \delta \lt 1$, 具体的等式可参考原始论文，这里不再展开。

当 $t = 1$ 也就是在最开始一次试验都没有的时候， $p(\theta)$ 会被初始化为 $\mathcal{N}(0, v^2I_d)$,

而每次选择 arm 的策略跟上面的 Bernoulli Bandit 类似：每个 arm 的 $p(reward|\theta)$ 分布分别产生一个 $\theta$, 然后选择 $x^t\theta$ 最大的那个 arm 进行试验。

小结

本文主要介绍了几种针对 EE 问题的策略，除了最简单的随机方法，UCB 和 Thompson Sampling 是这个问题两种比较典型的方法，两个方法的思想均是为每个 arm 计算出一个收益值，然后根据这个值进行 ranking 然后选择值最大的 arm。

UCB 采用的是频率学派的思想，计算的收益值是历史收益加上一个 bound，可以认为历史收益是 Exploitation，而 bound 则是 Exploration；而 Thompson Sampling 方法中每个 arm 的收益值会从一个分布中产生，没有明显的 Exploitation 和 Exploration，但也可以认为从分布中较大概率产生的值是 Exploitation ，而较小概率产生的值是 Exploration。另外，文中重点是介绍这些方法的具体做法，更多关于这些方法的理论基础和数学推导可参考下面这些文献。

参考：

开栏：智能决策系列
推荐系统的 EE 问题及 Bandit 算法
Reinforcement Learning: Exploration vs Exploitation
Multi-Armed Bandits and the Gittins Index
Boltzmann Exploration Done Right
Optimism in the Face of Uncertainty: the UCB1 Algorithm
Finite-time Analysis of the Multiarmed Bandit Problem
Exploring compact reinforcement-learning representations with linear regression
A Tutorial on Thompson Sampling
A Contextual-Ba ndit Approach to Personalized News Article Recommendation