超参搜索中的 Bayesian Optimization 方法

发表于 2019-07-10 标签机器学习

机器学习中存在着众多的超参数，如 model 中的超参，optimizer 中的超参，loss function 中的各种超参等，这些超参需要使用者根据经验设定，并根据训练结果进行调整，因为这些超参的最优值跟不同任务、不同数据集相关，没有一个非常通用的经验值。

这一步骤往往繁琐耗时，为了简化这一过程，有了 Hyperparameter optimization 的研究，其目的是自动搜索最优的超参。超参搜索最常见的方法是 grid search，random search，当然也有更高级的方法如基于启发式方法的 heuristic search、基于统计学的 bayesian optimization 等，本文主要介绍超参搜索中的 Bayesian Optimization 方法，这是超参搜索比较常见的做法，Google 也将这部分作为一个 service 提供在 Google Cloud 上。本文主要介绍 Bayesian Optimization 中的 GPR (Gaussian Process Regression) + GP-BUCB (Gaussian Process Regression-Batch Upper Confidence Bound) 方法。

更准确地说， Bayesian Optimization 应该是一个算法框架，其目的是为了推断那些不能显示给出函数形式的 black-box function，而在超参搜索中，这个函数指的是将超参数 \(x\) 映射至最终的收益 \(y\) 的那个函数，这里的收益不一定是 loss，还可以是 loss 与评估指标的融合，如在 ctr 预估中可以将 y 定义为：\(y = \alpha_1 \* auc - \alpha_2 \* logloss\)

常见的 Bayesian Optimization 方法由两部分组成，高斯过程回归 (Gaussian Process Regression, GPR) 和 EE (Exploration Exploitation) trade-off, 下面分别介绍这两部分的具体过程

高斯过程回归 (GPR)

首先，从名字上看，高斯过程回归是一种回归方法，而回归就是给一堆已知的 x 和 y，然后当拿出一个新 x 的时候，能够预测出对应的新 y，但是不同于常见的回归方法最终预测出一个值，高斯过程回归最终预测的是新的 y 的分布

那高斯体现在哪里？顾名思义，Bayesian Optimization 是一种贝叶斯方法，而贝叶斯方法往往少不了先验，而在这里高斯其实是作为一种先验，即我们认为所有的 y 服从一个零均值的多维的联合高斯分布（注意这里每个 y 自己也服从一个一维高斯分布），相比于一维高斯分布，多维高斯分布将原来的均值变为了均值向量，方差变为了协方差矩阵，（可参考多维高斯分布是如何由一维发展而来的？了解如何从一维高斯分布推广至多维高斯分布)

至于过程 (process), 则是指随机过程 (stochastic process), 这里指的是多个服从高斯分布的随机变量组成了一个随机过程，但是这里点对于我们理解 GPR 不重要。

推导 GPR 可从 Weight-space 角度或 Function-space 角度进行，具体可参考 Gaussian Processes for Machine Learning 中 p7-p35 部分，这里为了简单起见只从 Function-space 进行描述，并且会尽可能通过直观的方式描述这一点，某些符号与上面的 pdf 可能不一致

在训练集中，假设我们有 3 个 x, 记为 \(x_1、x_2、 x_3\), 以及这 3 个点对应的 y, 记为 \(f_1、f_2、f_3\)，由于假设所有的 y 服从一个均值为 0 的多维联合高斯分布，因此可写成如下形式 (下面图片摘自这篇文章）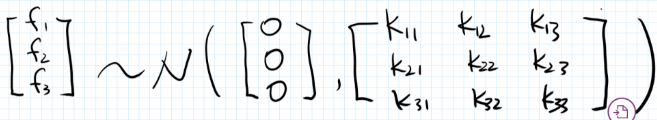

现在问题关键是模型的协方差矩阵 K 从哪儿来，为了解答这个问题，进行了另一个重要假设：

如果两个 x 比较相似（即离得比较近），那么对应的 y 值的相关性也就较高，即加入 x3 和 x2 离得比较近，则认为 f3 和 f2 的 correlation 要比 f3 和 f1 的 correlation 高。换言之，协方差矩阵是 X 的函数而不是 y 的函数

那么怎么衡量两个 x 比较相似？这个选择很多了，下面是一些简单的例子，在 GPR 中常用的是 RBF kernel（就是 SVM 中的那个 kernel，理论上，SVM 中的任意 kernel 在这里都适用）简单来说，RBF 隐式地对 x 进行了升维并计算内积，提升了表达能力。

协方差

\[\begin{align} k(x_1, x_2) = E[(x_1 - E(x_1))*(x_2 - E(x_2)] \end{align}\]

相关系数

\[\begin{align} k(x_1, x_2) = \frac{E[(x_1 - E(x_1))*(x_2 - E(x_2)]}{\sigma_{x_1}\sigma_{x_2}} \end{align}\]

RBF kernel

\[\begin{align} k(x_1, x_2) = \exp(-\frac{||x_1 - x_2||_2^2}{2\sigma^2}) \end{align}\]

则当有新的 \(x_\*\) 要预测新的 \(f^\*\) 时，由于假设所有的 y (即 f) 服从一个均值为 0 的多维联合高斯分布，因此可写成如下形式，而由于协方差矩阵是 \(x\) 的函数，因此，下图中的 \(K\) 和 \(K_\*\) 都可计算出来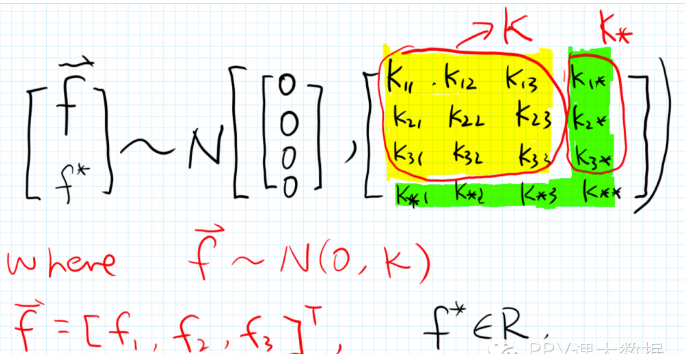

其中 \(K_\*\) 的计算方式如下，\(k\) 就是上面提到的衡量两个 \(x\) 有多近的函数，在 GPR 中也被称为 convariance function

\[\begin{align} K_\* = [k(x_\*, x_1), k(x_\*, x_2), k(x_\*, x\*_\*3)]^T \end{align}\]

有了所有 \(f\) 的联合分布，根据多维高斯分布的性质，可计算出 \(f^\*\) 的分布如下，即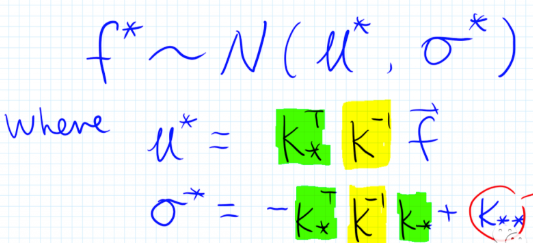

从上面的计算过程可知，GPR 的效果非常依赖于衡量两个 \(x\) 的相似度的函数 \(k\), 而 RBF kernel 中存在着超参 \(\sigma\), 因此 GPR 还会根据得到的样本进行 MLE，进而更新 RBF kernel 中的超参数，其中要最大化的是样本的 log marginal likelihood, 其定义如下

\[\begin{align} \log p(y|x,\theta) = -\frac{1}{2}\log|K| - \frac{1}{2} (y-\mu)^TK^{-1}(y-\mu)-\frac{n}{2}\log(2\pi)\end{align}\]

因此，得到已有的样本后，将上面式子中的协方差矩阵 \(K\) 中的超参数 \(\sigma\) 视为未知变量，便可通过梯度下降等方法更新超参数

sklearn 中提供的 GPR 的实验，具体的使用方法及实现可参考 GaussianProcessRegressor

通过上述的推导可知，对于每个新 \(x_\*\), GPR 会预估出这个 \(x_\*\) 对应的 \(y_\*\) 的分布 (分布的具体形式为高斯分布)，而分布中均值表示 \(y_\*\) 的预估值，方差则在一定程度上表示对这个预估值的置信程度（方差越大，预估值越不置信）

因此，GPR 的预估值天然就具备了 EE (Exploration&Exploitation) 的属性，而这也是 Bayesian Optimization 第二步需要解决的问题，解决的方法有很多选择，其中可以贪婪地选择均值最大的，也可以综合考虑均值和方差，这个选择的策略在 Bayesian Optimization 中也被称为 acquisition function；本文主要讲述其中的一种策略：UCB（Upper Confidence Bound)。

EE tradeoff

假设现在有了 10000 组候选超参，通过 GPR 分别预测出 10000 组对应的均值和方差，那么该选择哪一组超参？这个问题可以很自然地通过 MAB(Multi-armed bandit) 建模，而选择期望收益最高的策略在 Bayesian Optimization 中也被称为 acquisition function，acquisition function 有多种选择，其中最常用的便是 UCB

Gaussian Process Optimization in the Bandit Setting: No Regret and Experimental Design 中最早提出了一种应用在 GPR 中的 UCB 方法，也称为 GP-UCB，其方法的流程如下图所示

上面的算法流程中每次迭代都是选择出一个 \(x_t\) ，通过训练或实验获得其真实的 \(y_t\), 并根据真实的结果更新 RBF kernel 中的超参数；而选择 \(x\) 根据的是其对应的均值和方差的加权求和的值，其中方差权重的值 \(\beta_t\) 的选择跟 regret bound（MAB 中的概念）有关，上面的 paper 中证明了这一点，具体证明过程可参考原文，这里只给出最终的结论

即 \(\beta = 2\log(|D|t^2\pi^2/6\delta)\), 其中 \(|D|\) 为当前样本的个数，\(\delta\) 需要根据置信程度选择，\(\delta\) 越小，表示选择越为保守，更偏向于 Exploitation

GP-UCB 方法每次只能选择一个 \(x\) 进行试验，因此 Parallelizing Exploration–Exploitation Tradeoffs with Gaussian Process Bandit Optimization 中对 GP-UCB 进行了简单的改进，每次能够选择多个 \(x\) 并行进行试验，其算法流程如下

上面的 fb 函数定义为 \(fb[t] = \lfloor (t-1)/B\rfloor B\), 则 \(fb[0] = ...fb[B] = 0, fb[B+1] = ... fb[2B] = B\)，即每次选择 B 组超参进行同时搜索，然后才根据反馈更新各组超参对应的 y 的均值，这种方法与在 GP-UCB 中直接选择 B 个最大的区别是这种方法在这 B 次迭代中，每次都会根据选择了的 \(x\) 和 \(y\) 更新 RBF kernel 中的超参数，进而在下一次能够更新协方差矩阵

新广告或者说冷启动问题中也常常涉及到 EE 的问题，这里对两者的异同进行简单的比较

其中最主要的差别是在新广告的中每个 arm (一个新广告) 的收益是不能通过一次试验确定的，而在超参搜索中每个 arm (一组超参) 的收益通过一次试验就能确定了

在新广告的 EE 问题中，正是由于 arm 的收益是不确定的，所以才需要多次的试验结果来确定每个 arm 的期望收益

频率学派认为只要每个 arm 能够进行足够多次的实验，那每个 arm 的收益便可通过后验数据统计得到，但是正因为无法进行足够多次的实验，才会在不够置信的历史收益基础上增加一个 bound 作为 arm 的收益，而这就是 UCB 的主要思想，如果考虑每次请求上下文那就是 Lin-UCB

贝叶斯学派则认为每个 arm 的收益服从着特定的分布，首先会给每个 arm 一个收益的先验分布，然后通过试验获得似然并更新先验分布获得后验，然后后验作为下一次的先验；通过迭代这个过程让每个 arm 的分布更加接近真实分布，而这就是 Thomson Sampling 的思想，如果不考虑上下文，便是 Beta 先验 + Bernoulli 似然；如果考虑了上下文，便是 Gaussian 先验 + Gaussian 似然 n

关于这一类型的 EE 问题可参考 EE 问题概述

而在超参搜索的 EE 问题中，问题就没那么复杂了，只要超参选定了，那么只要用这组超参进行模型的训练或 AB 实验，其收益是确定的 (在其他实验条件基本确定下)

小结

本文主要介绍了超参搜索中的 Bayesian Optimization 中常用的 GPR+GP-UCB 组合。GPR 是一种贝叶斯回归方法，能够回归出 y 的分布而不是一个具体的值，其使用也不限于 Bayesian Optimization 中；而 GP-UCB 与冷启动新广告中的 UCB 等 bandit 算法也不完全相同，主要原因是在超参搜索中的一组超参 (arm) 的收益通过一次试验便能够确定了，而一个新广告（arm) 的收益在一次试验中并无法完全确定，其方法的区别可参考 EE tradeoff 部分。