《Bid Optimization by Multivariable Control in Display Advertising》阅读笔记
推荐与广告可以说是很多互联网公司的两个重要业务,其中推荐是为了 DAU 的增长,或者说流量的增长,而广告则是利用这些流量进行变现。两者的要解决的问题也很相似,都是在每条流量到来的时候,要从一个庞大的候选集中选出 topk 个候选返回,基本都采用 召回 + 精排 的架构,中间还可能插入粗排,本质上都是在效果与工程之间做 trade-off。
如果说两者技术上最大的 diff,笔者认为是出价,因为在广告场景中引入了广告主 (advertiser) 这一角色,因此我们除了考虑用户体验,还需要满足金主爸爸们的诉求(如跑量、成本等),才能带来持续的收入增长,而金主爸爸们表达其诉求的最直接的手段就是出价,其含义就是愿意为每个 click/convert 付出多少钱 (truthful telling)。这带出来的就是 bidding 这一研究领域,关于这个领域在 rtb-papers 中有很多相关的 paper。
本文主要讲的是 2019 KDD 阿里的 Bid Optimization by Multivariable Control in Display Advertising,这篇 paper 解决了出价的两个的核心问题:出价公式和调价策略,从最优的出价公式的推导到出价控制器的构建,文章的总体的建模思路非常值得学习,整个推导的 paradigm 能够推广到更一般的出价场景,实践性也较强,推荐读原文。
出价从技术上可认为主要由两大部分组成:出价公式和控制器,比如说常见的 cpc 出价公式是 bid * ctr, 最常见的控制器则是 PID。出价公式我们能比较好理解,那为什么要控制器来调价而不是按照广告主给的出价来投呢?笔者认为主要有以下两个原因
- 为了满足广告主的各种诉求;如需要匀速投放时,即在一天内均匀地花完预算,这样就需要通过控制器来控制运算花费曲线趋势与大盘流量曲线的趋势保持一致;如需要保成本时,需要通过控制器在成本高了时压价, 低了时提价;需要跑量同时允许在成本有略微上涨时,可以在成本可控的情况下更激进一点出出价
- ctr/cvr 的预估不是完全准确的;常见的 ctr/cvr 高估时,容易导致超成本,因为这时候计算出来的 ecpm = bid×ctr×cvr 也相当于是高估了;其根本原因是在 ctr/cvr 预估中没有一个绝对的 ground truth, 我们能拿到的是点击 / 转化与否,但是要预估的则是点击 / 转化的概率
前面提到,paper 中主要讲了两部分内容,最优出价公式的推导和控制器,下面描述的内容也会主要从这两方面进行描述
最优出价公式
paper 中要解决的场景是在保住点击成本和预算时,最大化广告主的在所有参竞价值 (value),因此这个优化问题可写成如下形式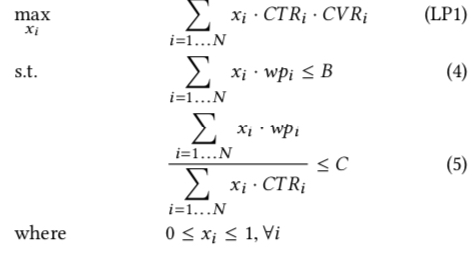
上式中的各个符号含义如下
- \(N\), 广告计划的总的可参竞次数 (opportunities)
- \(x_i\), 第 i 次竞价获胜的概率
- \(wp_i\), 第 i 次竞价的 winning price,即 bid price 要大于等于这个值才能获胜
- \(B\), 计划的总预算
- \(C\), 计划设置的点击成本
值得注意的是,我们不需要直接求解出上面的最优化问题的解,而只是需要求出取值为最优时的的解形式,然后作为最优出价公式,也就是说我们并不关心上面的 \(x_i\) 的最优解取值,而关心的是其他变量满足什么样的形式时,\(x_i\) 的解是最优的
paper 原始推导
paper 通过最优化中的对偶理论将上面的原问题 (primal problem) 转为对偶问题 (dual problem),如下图所示;对偶理论的详细描述可参考 最优化计算课程总结 中对偶理论这一节内容或 Duality Theory 这个讲义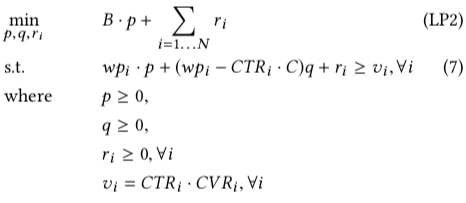
上图中的 \(p,q,r\) 都是对偶问题中变量,对应于原问题中的三类约束:预算,成本和对 \(x\) 的范围的约束,根据互补松弛定理 (Complementary Slackness) ,可得到下面两个式子,互补松弛定理的详细描述同样可参考上面的两个链接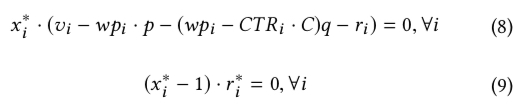
上面的公式中 \(x_i^{*}\) 和 \(r_i^{*}\) 分别表示原问题和对偶问题的最优解,后面带 * 上标的符号均表示最优解,至此为止,上面都是基于最优化理论推导出来的一些公式,但是接下来这一步就有点跳了,paper 中直接令最优出价公式为
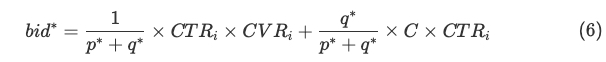
则上面那些公式中表示给广告主带来的价值 \(v_i\) 可写成 \(v_{i} = bid_{i} - wp_{i}\), 将公式(6)代入这个式子,再将 \(v_i\) 代入上图中的公式 (8),可得到下面的公式(10)及其分类讨论的结果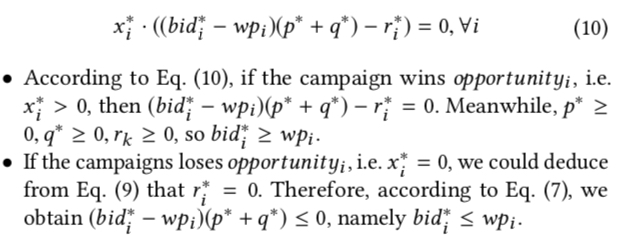
上面的两个分类讨论的结果实际上表明了无论最优解 \(x^*\) 是赢得这次竞价 (\(x=1\)) 还是输掉这次竞价 (\(x=0\)),按照公式 (6) 进行出价时,总能保证解是最优的
另一种推导思路
之所以说上面最后的推导有点跳,是因为公式 (6) 所表示的那一坨最优出价公式是怎么给出来的?随便拍脑袋似乎不太可能,paper 中并没有针对这一点详细描述,笔者在这里尝试提供另一个求解的思路,就是利用拉格朗日对偶来推导出最优出价公式,关于这部分内容可参考 凸优化总结 中的拉格朗日对偶部分
对于原问题即上图中的 LP1, 可写出其増广拉格朗日函数为 (暂时忽略 \(x\) 的值的约束)
\[\begin{align} L(x,p,q) = \sum_{i=1\dots N}-x_iCTR_iCVR_i + p(\sum_{i=1\dots N}x_iwp_i-B) + q(\sum_{i=1\dots N}x_i(wp_i-CTR_iC)) \end{align}\]
上式中的 \(p>=0,q>=0\),则原问题可写成如下形式, 详细推导过程可参考上面的凸优化总结的链接
\[\begin{align} \max_{p, q}\min_{x_i}L(x,p,q) \end{align}\]
如果是要求出这个问题的解,还需要转为拉格朗日对偶问题,通过 SMO 等算法进行求解,但是我们这里不需要确切的解,而是只需要最优解的表达式,因此可令 \(\frac{\partial{L(x,p,q)}}{\partial{x}}=0\), 求解可得
\[\begin{align} wp_i = \frac{1}{p+q} × CTR_{i} × CVR_{i} + \frac{q}{p+q} × C × CTR_{i} \end{align}\]
可以看到,winning price \(wp_i\) 推导出来的形式跟上面给的公式 (6) 中的最优出价公式的形式是一样的!!!
但是上面的推导中的仍有一些问题,上面求解的是最优的 \(wp_i\),bid 这个变量没有显示地出现在增广拉格朗日函数中,但是可近似认为两者是相等的;其次是,\(x_i\) 本身的约束 (即取值在 0~1 之间) 没有显式的考虑进增广拉格朗日函数中,针对这一点,笔者的理解是在解决最优化问题时可以忽略某个条件,然后在求解出来之后基于这个条件做分类讨论,而这一部分实际上就是原始 paper 在推导出公式 (10) 后做的分类讨论。
小结
综合考虑上面两部分的推导,可以得到最优的出价公式如上面公式 (6) 所示,公式中的 \(p\) 和 \(q\) 是两个超参,是对偶问题中需要求解的变量,如果需要求解,意味着需要拿到参竞的所有后验数据,但是实际中在参竞时就需要通过这些参数给出参竞的 bid,这似乎就成了一个先有鸡还是先有蛋的问题了,后面会通过控制器描述如何解决这一问题,具体思想就是不直接求解原始的最优化问题,而是通过近似的方式来逐渐逼近最优解
回到公式 (6) 的最优出价公式,如果将其写成 c_bid * ctr 的形式,有如下公式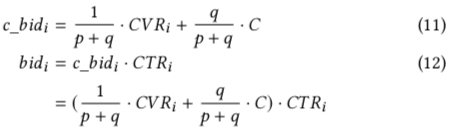
如果更直观的画出来如下图所示,从图中可知,哪怕 CVR 为 0 时,bid 也不一定为 0,这跟常见的 ecpm = bid×ctr×cvr 不太一样,这可理解为一些 cvr 低但是 ctr 高的流量也是可以拿的;此外,c_bid 的直线会过两个定点: (-qC, 0) 和 (pC, C), 后面在控制器中会详细描述这两个点的具体含义。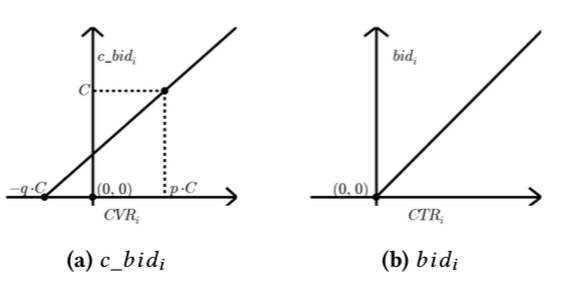
调价策略
前面提到,最优出价公式中的 \(p\) 和 \(q\) 的最优解求解需要拿到参竞后的后验数据,但是 bid 是要在参竞的时候就给出来,因此这就成了一个先有鸡还是先有蛋的问题。针对这个问题,最直观的一个想法是,我们 可不可以用历史数据来求出最优的 \(p\) 和 \(q\), 然后应用到下一时刻的出价中? paper 中也提到了这一点,答案是 no,因为这个方法假设了参竞流量的分布是基本不变的,但是竞价环境是一个受多个因素影响的动态变化环境 (包括参竞流量、ctr、cvr 等),即历史的最优不会是未来的最优。在实际的实践中,笔者的实践经验的确是这样的。
由于竞价环境是实时变化的,因此需要动态调价,在调价策略中,需要先明确两个点:调控的目标和调控的变量。以最经典的 PID 控制器为例,如下图所示,调控的目标是 \(r(t)\) 与 \(y(t)\) 尽可能接近,调控的变量是 \(x(t)\)。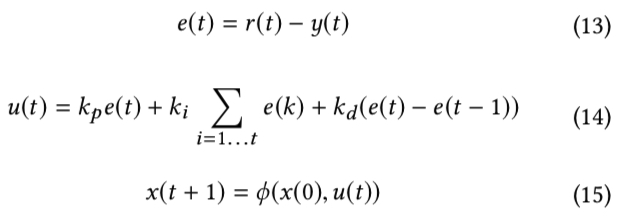
每次调整变量时,需要通过公式 (13) 计算出当前的 error,然后通过公式 (14) 计算出控制型号 \(u(t)\)(其中 \(k_p\)、\(k_i\)、\(k_d\) 是三个拍定的超参),最后利用 \(u(t)\) 通过公式 (15) 的调控公式 (actuator model) \(\phi(x(0), u(t))\) 得到最终调整后的值
PID 对于单变量的控制可以说是比较常用和有效的方法,但是我们的上面提到的问题是一个多变量控制问题,其中控制变量是 \(p\) 和 \(q\),控制目标是控制好预算花费并保点击成本 ; 对于这个问题,一个很直观的想法就是通过双 PID 分别进行独立调控,但是这些控制变量之间往往不是相互独立的,因此双 PID 不是最优的 , 后面会详细描述这一点。
参数分析
下面首先会分析控制变量 \(p\) 和 \(q\) 分别影响哪些控制目标
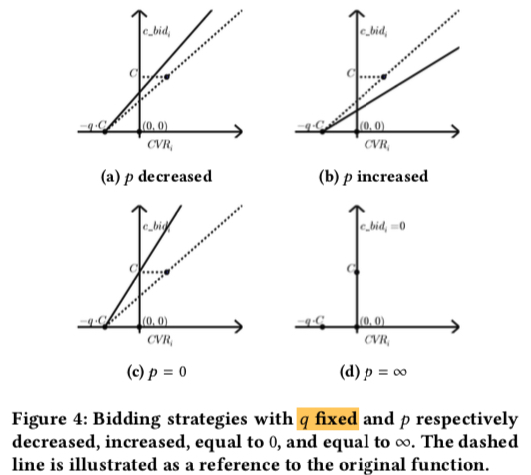
如下图 4 是固定 \(q\),改变 \(p\) 时,c_bid 的变化,其中虚线表示改变前的出价,实线表示改变后的出价;从图中可知
- 出价的直线始终通过 (-qC, 0) 这个点
- 随着 \(p\) 的减小,出价的直线的斜率逐渐增大,表示出价更高,同时消耗的 budget 也会更多;而随着 \(p\) 增大导致的结果则是刚好相反
- 当 \(p\) 取最小值即 0 时,表示没有 budget 的限制,出价公式退化为 \(C×CTR+\frac{1}{q}CTR×CVR\), 公式第一项可以认为是只按照点击出价来保点击成本 \(C\),第二项则是为了达到 \(\max v=CTR×CVR\) 的目标
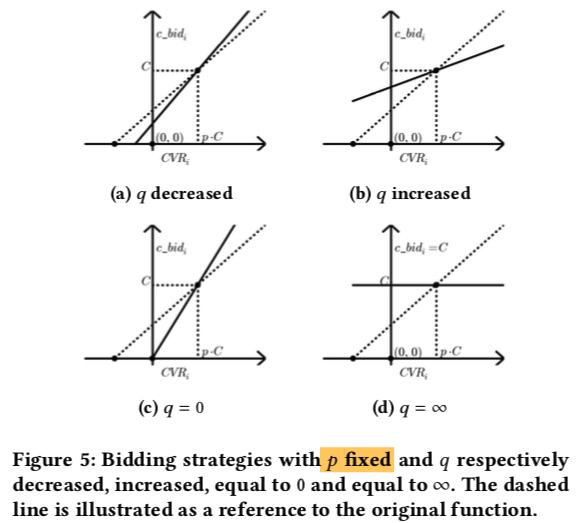
同理可画出下图 5 中固定 \(p\),改变 \(q\) 时,c_bid 的变化; 从图中可知
- 出价的直线始终通过 (pC, C) 这个点
- 随着 \(q\) 的减小,出价的直线的斜率逐渐增大,表示对于 CVR 比 pC 更高的流量出价更高,CVR 比 pC 更低的流量出价更低 , 而随着 \(q\) 增大导致的结果则是刚好相反
- 当 \(q\) 取最小值即 0 时,表示没有点击成本的限制,此时的出价公式退化为 \(\frac{1}{p}CTR×CVR\),代表出价成本的符号 \(C\) 没有出现的出价公式中,总体表示要达到 \(\max v=CTR×CVR\) 的目标,同时通过 \(q\) 来控制预算
控制器
通过上面的分析可知,参数 \(p\) 是被用来控制预算的使用,而参数 \(q\) 则是被用来控制点击成本;其实这与我们上面推导最优出价公式时对应的约束条件是一致的。
因此,一种最简单的策略是用两个独立的 PID 来分别调控变量 \(p\) 和 \(q\),调控的目标则是预算和点击成本。如下图所示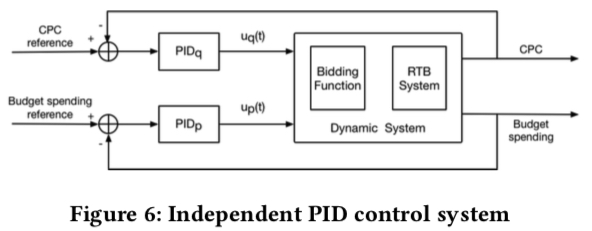
但是我们前面也提到,这两者并不是完全独立的,比如说为了保点击成本进行提价或降价也会影响到预算的使用,反之亦然。因此两个完全独立的 PID 并不是最优的选择,而是在控制中要考虑两个变量相互的影响
Model Predict Control(MPC) 中有关于这类问题的研究,但是 paper 中并不直接采用这个方法,因为 paper 中认为 "modelling the highly non-linear RTB environment is costly and even impratical"; 而是通过一个线性模型去拟合。笔者认为其可行的原因是调控往往会分为多个时间片,然后在每个时间片内进行调控,而在每个时间片内用直线去拟合,理论上只要把时间切得足够小,最终总体也能拟合出非线性的曲线。
主要的建模思想是通过两个 linear regression model 直接建模变量 \(p、q\) 和目标 cost、CPC 的关系 (即原文的 model the bidding environment with respect to cost and CPC)具体的做法如下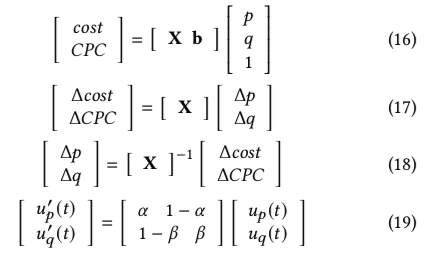
上图中的公式 (16) 里的 \(X\) 和 \(b\) 分别表示 2×2 的矩阵和 2×1 的矩阵,如果展开后其实就是两个 linear regression model
进一步地,公式 (17) 表示的是给定需要控制的目标 \(\Delta cost\) 和 \(\Delta CPC\)(调价是分时间片进行调控的,在每次调控前都可以根据当前累积消耗和成本等后验数据,进而进行计算当前时间片需要调控得到的 \(\Delta cost\) 和 \(\Delta CPC\)),可以对 p 和 q 分别进行 \(\Delta p\) 和 \(\Delta q\) 的调控达到目标,笔者这里有个疑问,为什么这里的 b 可以被约去,
虽然 paper 中没有直接提到,但是笔者认为其实到了公式 (17) 已经可以进行调控了,只是调控的方式跟 paper 中不太一样,这里简单描述一下。首先需要获取公式 (17) 中 \(X\),而 \(X\) 中的参数其实是可通过训练数据获取,训练的数据集 从当前时间往前的若干个个时间片内的 (\(\Delta p\), \(\Delta q\), \(\Delta p\), \(\Delta q\)),然后 \(X\) 就可以通过常规的训练方式获取;这样在每个时间片调价时,只需要计算好的 \(X\) 和下一时间片的调控目标:\(\Delta cost\) 、 \(\Delta CPC\) ,便能通过 grid search 得到最优的 \(\Delta q\) 和 \(\Delta p\)。
公式 (18) 是在公式 (17) 基础上乘上矩阵 \(X\) 的逆便得到;公式 (19) 则是 paper 中提出的调控方式:首先通过上面的 PID 调控公式 (14) 可以将公式 (18) 中的 \(\Delta cost\) 、 \(\Delta CPC\) 变为 \(u_{p}(t)\)、\(u_{q}(t)\); 同时只用两个变量 \(\alpha\) 和 \(\beta\) 来近似矩阵 \(X\) 的逆(理论上应该有 4 个的),并认为 \(p\)、\(q\) 的 control signal (通过公式 (14) 获取) \(u'_{p}(t)\)、\(u'_{q}(t)\) 是 \(u_{p}(t)\)、\(u_{q}(t)\) 的线性组合;paper 称这样做的好处是 makes the controller more robust and stable against the changing environment, paper 中称 \(\alpha\) 和 \(\beta\) 是从训练集中获取的 (详见下面的实验效果环节)
因此,根据公式 (19), 总体的调控系统变为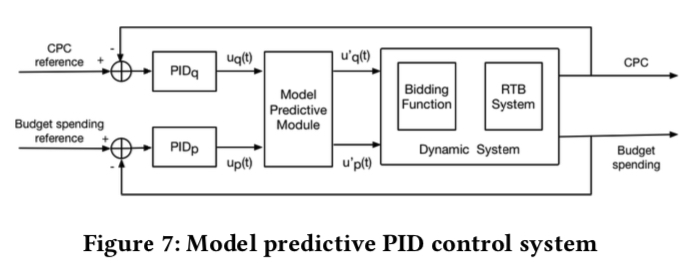
实验设置与效果评估
基本设置
paper 中并没有进行在线实验,而是通过离线方式进行评估
采用的数据集是 taobao 40 个计划总共 20M 条 bid log,每条 bid log 的关键信息是 \(wp_i、 CTR、CVR\);同时根据时间划分了训练集和测试集
评估指标主要有两个
- \(CPC_{ratio}\): 表示保住点击成本的计划的比例
- \(Value_{ratio}\):表示按最优出价公式重新投放时,每个计划获取的 value 与其理论最优的比值 (\(\le 1\))
实现细节
除此之外,paper 中通过 PID 计算 control signal 时,会对 err 进行加权,而传统的 PID 中所有的 err 的权值都是一样的,其加权方法如下公式 (21) 所示,而前一章提到的 \(u_{q}(t)\) 计算方式如公式 (22) 所示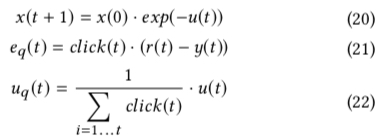
除了对 err 进行加权,上面的公式(20)也很有意思,就是每次通过 control signal 调整目标 zhi 值 \(x\) 时,不是基于上一次的值 \(x(t)\),而是基于最开始的值 \(x(0)\)
此外,调价的频率是每小时调整一次,PID 中涉及的超参 (\(k_p、 k_i、 k_d\)) 以及公式 (19) 中的 \(\alpha\) 和 \(\beta\) 都是在训练集中通过 grid serach 找到的
因此,总体的实验步骤如下
- 基于训练数据集计算出最优的 \(p\) 、\(q\) 作为其初始值
- 在测试数据集上用上面的最优出价公式和调价策略进行模拟竞价
(3)当计划的 budget 消耗完或者所有的日志回放完成则终止
效果对比
实验效果如下图所示,其中图 8 是 budget 消耗的情况,图 9 是成本情况,同时左边的图是实时指标,右边的图是累积指标;从图中可知,budget 消耗的幅度无论是实时还是累积都拟合得比较好,而点击成本虽然在实时上由波动,但是累积的成本是比较稳定的。
除此之外,paper 还与其他的一些方法进行了比较,结果如下图所示,其中 I-PID 和 M-PID 是本文提出的方法,分别表示 PID 是否相互独立的,从结果可知,采用了 paper 中的出价公式且考虑控制变量的关系的调价方式的效果是最好的,也印证了我们前面提到的两个完全独立的 PID 并不是最优的选择,而是在控制中要考虑两个变量相互的影响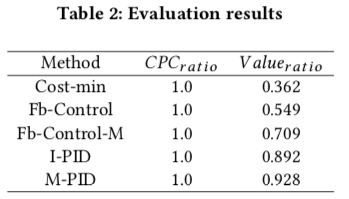
小结
综上,这篇 paper 首先将要求解的方法建模成一个最优化的问题,然后通过对偶理论求解出这个最优化问题的最优解的形式,而不是它的解;接着描述了多变量调控系统中一种考虑控制变量间相互关系的调控策略,并通过实验结果证明这种策略的效果要优于只通过两个独立的 PID 分别调控的效果;美中不足的是没有做在线实验,毕竟离线实验的环境变基本就定下来了,重新进行竞价也不会改变这个环境,不像线上变化那么剧烈;但是 paper 中的总体建模思路还是非常值得学习的,可以作为一个 paradigm 推广到更一般的出价场景。