Delayed FeedBack In Computational Advertising
转化是有延迟的,即在点击发生后过一段时间用户可能才会发生转化,且往往转化漏斗越深,延迟的时间越长;在计算广告中,delayed feedback 主要影响下面两个场景
- CVR 模型的训练
- 基于后验的调价策略
对于场景 1,影响体现在(1)过早把样本送入模型,把最终会转化但是还没回传 label 的事件当做负例,导致模型低估(2)过晚把样本送入模型,即让所有样本都等待一个足够长的时间才送入模型,导致模型没能及时更新
对于场景 2,影响体现控制器控制 cost/value=target 时,分母会小于实际值,导致控制的不稳定
本文主要介绍三篇 paper 针对这个问题在场景 1 的一些解决思路,其中涉及到的一些方法也能应用到场景 2 中(而如果问题 1 能被较好地解决,也能基于预估值而不是后验数据进行调价)
第一篇 paper 是较早提出的一个解决方法,引入了一个隐变量辅助建模,同时对延迟时间单独建模,总体建模思路比较值得学习
第二篇 paper 是对第一篇 paper 的拓展,第一篇 paper 是通过指数分布建模回传延迟的时间的,而这篇 paper 则借鉴了 KDE (Kernel density estimation) 来学习任意分布去建模回传延迟时间
第三篇 paper 则是比较了几种方法在离线数据和在线实验的效果,改动主要是在 loss function 上;其中就包括了第一篇 paper 的方法,以及其他一些利用了 positive-unlabeled learning/importance sampling 等方法推导出来出新的 loss
Modeling Delayed Feedback in Display Advertising(2014)
这篇 paper 是 criteo 在 2014 年发表的一篇对 delayed feedback 建模的 paper,建模思路比较值得学习。针对这篇 paper 可参考之前写过的一篇文章
《Modeling Delayed Feedback in Display Advertising》 阅读笔记
A Nonparametric Delayed Feedback Model for Conversion Rate Prediction(2018)
这篇 paper 是在第一篇 paper 基础上对回传延迟函数做了改进,第一篇回传延迟使用了指数分布来建模,这里则借助了 KDE(Kernel density estimation) 的思想用任意分布来代替第一篇 paper 的指数分布,而这正是 paper 名字中 nonparametric 意思的含义。
基本符号定义跟第一篇 paper 差不多
Paper 中主要通过 Survival analysis 的方法来推导,简单来说,survival analysis 主要研究如下领域
Survival analysis is a branch of statistics for analyzing the expected duration of time until one or more events happen, such as death in biological organisms and failure in mechanical systems.
Paper 中使用到的 survival analysis 概念和推论如下
第一篇 paper 其实也用了上面的推论,\(f(t)\) 是指数分布的 pdf,\(s(t)\) 是指数分布的 cdf,而 \(h(t)\) 则是第一篇 paper 中的 \(\lambda(x)\)
而从上面的表达可知,求解出 \(s(t)\) 的关键是求出 hazard function \(h(x)\), hazard function 的含义是当前时刻第一次发生事件的 event rate; 相比于第一篇直接令 \(h(x) = \lambda(x) = w\_dx\), 这里借鉴了 Kernel density estimation 的思想将 hazard function 写成如下形式(\(L\) 是一个超参,表示时间轴上的 \(L\) 个 pseudo-points)
\[\begin{align} h(d_i; x_i, V) = \sum_{l=1}^{L}\alpha_l(x_i;V)k(t_l, d_i) \end{align}\]
下图更直观地描述了这种形式是如何拟合任意分布的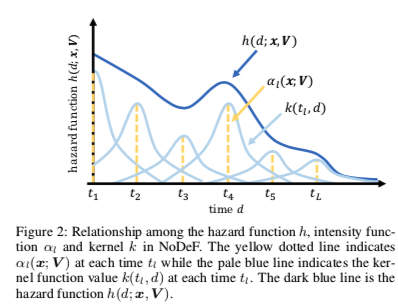
上面中的 \(\alpha_l, k\) 定义如下,直观来看,\(\alpha_l\) 表示当前的 pseudo-point 对总体的 hazard function 的贡献,\(k(t_l, \tau)\) 表示离当前的 pseudo-point \(t_l\) 越近的训练样本,对当前的 pseudo-point \(t_l\) 的参数 \(V_l\) 的影响越大(想象 bp 时各个 \(V_l\) 的 gradient)
\[\begin{align} \alpha_l(x_i; V) = (1+\exp(-V_{l}^{T}x_i))^{-1} \end{align}\]
\[\begin{align} k(t_l, \tau) = \exp(-\frac{(t_l-\tau)^2}{2h^2}) \end{align}\]
写出了 hazard function 后,根据公式(2)有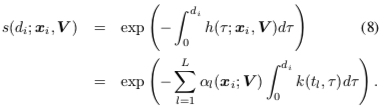
则 paper1 的的回传延迟概率可写成如下形式
\[\begin{align} p(d_i|x_i, c_i = 1) = s(d_i; x_i, V )h(d_i; x_i, V) \end{align}\]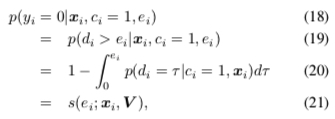
训练的算法就跟 paper1 中的 EM 算法一样
上面这种形式是借鉴了 KDE 的思想,KDE 可以理解为一种可写出任意分布的 pdf 的方法,关于这部分的推导这里有一个直观的回答:什么是核密度估计?如何感性认识?
Addressing Delayed Feedback for Continuous Training with Neural Networks in CTR prediction(2019)
这是 Twitter 发的一篇 paper,主要对比了几种方法在 delayed feedback 问题上的效果
Faked nagative weighted
Delay feedback 的问题也可以从另一个角度去理解,观察到的样本的分布是 biased distribution \(b\), 但是需要求解真实的样本的分布 \(p\) 的期望;而 importance sampling 是解决这个问题的一个方法,这个方法在 Wikipedia 上的简单介绍如下
In statistics, importance sampling is a general technique for estimating properties of a particular distribution, while only having samples generated from a different distribution than the distribution of interest
zhihu 上一个更通俗的解释见 重要性采样(Importance Sampling),则 paper 中的可将真实分布的期望写成如下形式
\[\begin{align} E_p[\log f_{\theta}(y|x)] = E_b[\frac{p(x,y)}{b(x,y)} f_{\theta}(y|x)] \end{align}\]
即在观察到的 biased distribution \(b\) 上对样本进行加权 \(w(x,y) = \frac{p(x,y)}{b(x,y)}\),则 loss function 可写成如下形式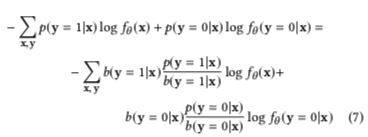
这个方法会将所有的样本在一开始都当做负样本,然后在正样本回传时多传一个正样本,假设 \(N\) 是全部样本,\(M\) 是其中的正样本,则有
\[\begin{align} b(y=1|x) = \frac{M}{M+N} = \frac{\frac{M}{N}}{1+\frac{M}{N}} = \frac{p(y=1|x)}{1+p(y=1|x)} \end{align}\]
\[\begin{align} b(y=0|x) = 1- b(y=1|x)= \frac{1}{1+p(y=1|x)} \end{align}\]
即上面公式 (7) 可被写成下面公式 (10), 即需要给分布 \(b\) 中的正样本加的权重为 \(1+p(y=1|x)\), 负样本的权重为 \(p(y=0|x)(1+p(y=1|x))\)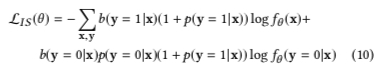
但是这里的 \(p\) 是未知的,因此 paper 中利用了模型的预估值 \(f_{\theta}\) 来近似
此外,importance sampling 也被应用在强化学习中的 off-policy 策略中,简单来说就是通过行为策略 (behavior strategy) \(b\) 产生的序列分布来优化目标策略 (target strategy) \(π\) 价值函数,关于 on-policy 与 off-policy 的区别可参考这个回答 强化学习中 on-policy 与 off-policy 有什么区别? )
Fake negative calibration
这个方法直接让模型学习 biased distribution \(b\), 然后基于上面 Faked nagative weighted 中推导出来的公式反推出 \(p(y=1|x)\) 的概率,即由
\[\begin{align} b(y=1|x) = \frac{M}{M+N} = \frac{\frac{M}{N}}{1+\frac{M}{N}} = \frac{p(y=1|x)}{1+p(y=1|x)} \end{align}\]
可推出
\[\begin{align} p(y=1|x) = \frac{b(y=1|x)}{1-b(y=1|x)} \end{align}\]
这种方法可以认为是一种 post calibration,除此之外,也有一种方法是在训练的时候就做了纠正的,也叫做 prior correction,基本思路就是在训练的时候对预估的 logit 做一层转换,简单推导如下
假设真实的分布下,正样本的数量是 \(P\),负样本的数量是 \(N\),
则 serving 是输出的概率值应该是
\[\begin{align} \frac{P}{P+N} = \frac{1}{1+e^{-x}} \end{align}\]
但是在 training 时,由于上面的机制使得每条样本都会以负样本的形式出现一次, 同时假设会对负样本采样,采样率为 \(r\), 则有
\[\begin{align} \frac{P}{r*(P+N)+P} = \frac{1}{1+e^{-x^{*}}} \end{align}\]
通过对上面的变换有
\[\begin{align} \frac{P}{r*(P+N)+P} = \frac{P/(P+N)}{r+P/(P+N)} = \frac{1/(1+e^{-x})}{r + 1/(1+e^{-x})} \end{align}\]
则令
\[\begin{align} \frac{1/(1+e^{-x})}{r + 1/(1+e^{-x})}=\frac{1}{1+e^{-x^{*}}} \end{align}\]
可推导出
\[\begin{align} x^{*} = -(\ln r+ \ln(1+e^{-x})) \end{align}\]
即在训练时计算 logit,不使用 \(\frac{1}{1+e^{-x}}\) 而是使用 \(\frac{1}{1+e^{-x^{*}}}\)
Positive-Unlabeled Learning
paper 关于里面基本没有推导,详细的推导可参考 Learning Classifiers from Only Positive and Unlabeled Data, 基本思路跟第一篇比较像,这里就不详细展开了,主要引用了里面一些关键的推导步骤
A key assumption about the training data is that they are drawn randomly from \(p(x,y,s)\), and for each tuple \(< x,y,s >\) that is drawn, only \(< x,s >\) is recorded. Here \(s\) is the observed label and \(y\) is the actual label, which might not have occurred yet. Along with this, it is assumed that labeled positive examples are chosen completely randomly from all positive examples, i.e. \(p(s = 1|x, y = 1) = p(s = 1|y = 1)\)
基于上面的 assumption 有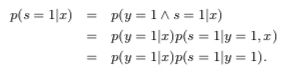
The value of the constant \(c = p(s = 1|y = 1)\) can be estimated using a trained classifier \(g\) and a validation set of examples. Let \(V\) be such a validation set that is drawn from the overall distribution \(p(x, y, s)\) in the same manner as the nontraditional training set. Let \(P\) be the subset of examples in \(V\) that are labeled (and hence positive). The estimator of \(p(s = 1|y = 1)\) is the average value of \(g(x)\) for \(x\) in \(P\). That is \(\frac{1}{n}\sum_{x \in P}g(x)\)
求解环节,所有样本的 期望 /likelihook 可写成如下形式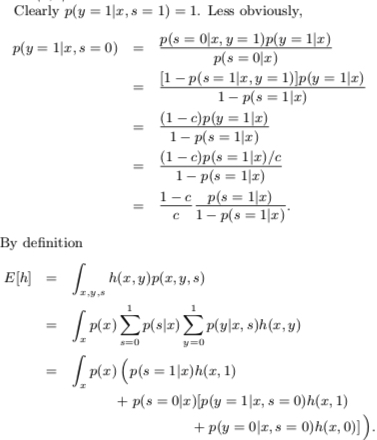
则最终的 loss 函数形式如下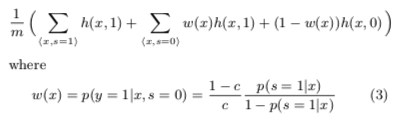
总结
本文主要介绍了对 delay feedback 问题的几种解决方法,其中第一篇 paper 引入了一个隐变量,同时对转化延迟和转化分别建模,建模思路比较值得学习;第二篇 paper 则是对第一篇 paper 的转化延迟模型做了改进;第三篇则介绍了几种在一开始将所有样本都当做负样本,并在正样本回传的时候再进一次模型,但是这样会导致 training 和 serving 不一致(正负样本比例不一致),对此 paper 也提出了几种解决方法。