Exposure Bias In Machine Learning

发表于 标签 ，

机器学习本质上是在学习数据的分布，其有效性的假设是模型 training 和 serving 时的数据是独立同分布 (Independent and Identically Distributed, IID) 的，但是在实际应用中，由于采样有偏、具体场景等约束， training 的样本与 serving 时的样本并不是 IID 的。在广告场景下，最典型的就是训练 cvr 模型时，训练样本都是 post clicked 的，但是 serving 时，cvr 模型面临的是所有被召回的样本；这类问题也被称为 exposure bias 或 sample selection bias，除了 exposure bias，position bias 等也是常见的 bias。

本文首先会简单介绍一些机器学习中的常见 bias，并着重介绍上面提到的 exposure bias (也叫 sample selection bias) 的在当前的一些解决思路， 笔者将其总结为 Data Augmentation、IPS 和 Domain Adaption 三大类方法。

Bias In Recommender System

除了本文要重点介绍的 exposure bias，这篇综述 Bias and Debias in Recommender System: A Survey and Future Directions 描述了当前的推荐系统中存在的若干种 bias，paper 将当前的推荐系统划分为 User、Data、Model 三个大模块，并将各个模块的 iteraction 导致的 7 种 bias 归纳成下图

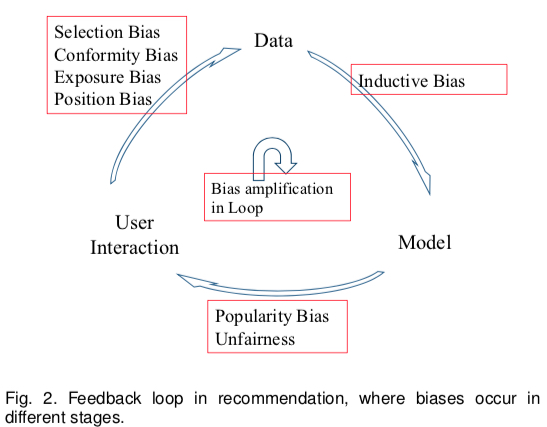
Bias in ML
  • User->Data: 产生训练数据的过程，也是 Bias 的最主要来源
    • Position Bias (implicit)：用户更倾向于和位置靠前的物品进行交互
    • Exposure/Observation Bias (implicit)：带标签的数据都是曝光过的，未曝光的数据无法确定其标签
    • Selection Bias (explicit)：用户倾向于给自己喜欢或者不喜欢的物品进行打分 (导致 exposure bias 的一个重要原因，不少 paper 将这个 bias 也当做 exposure bias)
    • Conformity Bias (explicit)：用户打分的分数倾向于和群体观点保持一致
  • Data->Model: 利用数据训练出模型的过程
    • Inductive Bias: 指的是模型为了泛化性而做出的一些 assumption，如 Occam's razor，SVM 假设线性可分的 assumption 等，这个 bias 没有带来显示的缺陷
  • Model->User Interaction: 指的是模型预估的过程
    • Popularity Bias：指的是长尾效应，热门物品会得到更高的曝光概率，因为模型会更倾向于推荐这些物品（unbalanced training data 引起）
    • Unfairness: 一些预估结果带有性别歧视、种族歧视等（unbalanced training data 引起

上面的各种 bias 的起因、影响以及一些解决思路可归纳为下表

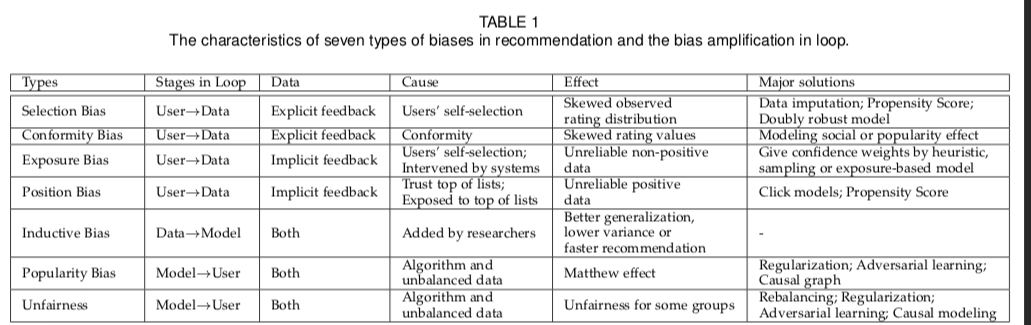
Bias details Table

可以看到，上面这些 bias 并不是孤立的，而是相互影响和恶化的，其中 position bias 和 exposure bias 又是最为常见且相关研究较多的一个领域，下面主要详细描述一些应对 exposure bias 的方法，值得注意的是，这里的 selection bias 跟 exposure bias 面临的问题是一致的，因此这里的方法也会一并归纳； bias 相应的方法可以参考上面的 paper。

Solutions to Exposure Bias

exposure bias 也被称为 Sample Selection Bias (SSB), 本质上是一个 training 和 serving 不一致的问题。这个问题往往是由于具体业务场景的限制，导致 training data 中的样本只是其 serving 时的很小一部分，因为其他的样本没被曝光 / 点击，导致了无法得到其 label。

如文章开头提到的 cvr 模型，对于那些不被点击的样本是无法得知其是否被转化的；同样地，在 ctr 模型中，那些没有曝光机会的样本是无法得知其是否被点击的了；但是在 serving 阶段，ctr/cvr 模型面对的是所有的样本，而其中有很多是从未曝光过的，因此便导致了一个 training 与 serving 不一致的问题。

针对这个问题，当前有以下几种解决思路 (不限于上面综述的 paper)

  1. Data Augmentation：这个是最朴素的想法，就是尽可能将那些没进入训练数据集的样本利用上，因此不少研究也是给 unobserved/unclicked 的样本打上一个相对准确的 label；而这里面也主要分为下面三类方法
  • 最粗暴的是把所有未曝光的样本当做 negative sample，然后基于不同策略给这些样本不同的权重
  • 训练一个 imputation model，然后通过 imputation model 来预估未曝光样本的 label
  • 通过 multitask 的方式建模，训练使用前一转化目标的全量样本 (ESMM)

  1. IPS(Inverse Propensity Score): 这个方法的假设是样本被曝光或点击服一个伯努利分布，然后从概率论推导出：只要给每个曝光的样本加权 (权重即为 inverse propensity score)，最终在曝光的样本上求得的期望等于在全量样本上的期望；实际上，这个方法的思想就是 importance sampling

  2. Domain Adaption: 类似 transfer learning 的思想，将曝光 / 点击的样本视为 source domain，全部样本视为 target domain；通过 domain adaption 的一些方法去进行 debias

Data Augmentation

上面提到了，最朴素的想法是将那些未被观测到的样本利用上，而这里面又可分为三大类方法：all nagative with confidence、imputation model 和 multitask learning

all nagative with confidence

第一类方法是将所有未被观测到的样本都当做负样本，而这里的核心是如何给每个样本一个合理的 confidence，其实就是样本的加权，上面提到的综述中介绍了三种方法，分别是 Heuristic、Sampling、Exposure-based model

  • Heuristic 尝试将 user activity level、user preference、item popularity、user-item feature similarity 等作为 (user, item) pair 的 confidence, 其思想都是认为用户活跃度越高、商品越热门、用户 - 商品匹配度越高，该样本的可信度 (confidence) 越高；但是这种方法往往可行性不够高，因为这个 confidence 实际的值是比较难获取的，其量纲以及需要对庞大的数据集都生成这个 confidence，难度是很大的。

  • Sampling：TODO

  • Exposure-based mode：TODO

imputation model

第二种方法也很直观，就是训练一个 imputation model 为那些未曝光 / 点击的样本打上标签，然后基于这些 imputed label 来训练模型；而 imputation model 可单独训练，也与目标的模型做 joint
training；这个方法的弊端也很明显，就是生成的 imputed label 缺少绝对的 ground truth 来衡量其效果，实际上，这个是所有直接为样本生成 label 的方法的弊端。

multitask learning

第三种方法是基于 multitask 的方法，主要思想就是同时建模当前的任务及其更浅一层的任务，进而间接利用那些没被曝光 / 点击的数据；其中为人熟知的是阿里在 2018 年发表的 ESMM, Entire Space Multi-Task Model: An Effective Approach for Estimating Post-Click Conversion Rate，这篇 paper 主要针对的是 cvr 模型中缺少未点击的样本带来的 bias，增加了两个 auxiliary task (CTR 和 CTCVR) 来缓解这个问题，总体的模型结构如下图所示

ESMM

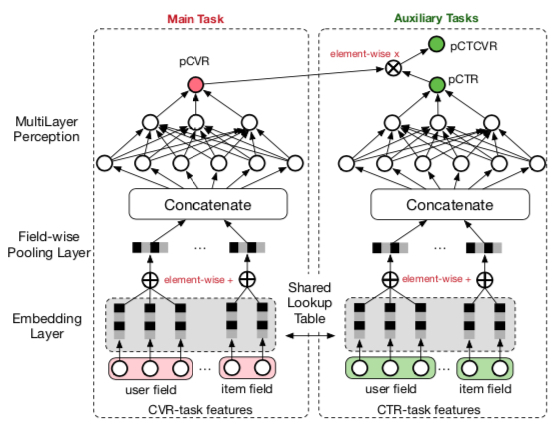
训练的 loss function 如下所示 (\(y\) 表示点击事件，\(z\) 表示转化事件)

\[\begin{align} L(\theta_{ctr},\theta_{cvr}) &= \sum_{i=1}^{N}l(y_i,f(x_i;\theta_{ctr})) \notag \\\ &+\sum_{i=1}^{N}l(y_i\& z_i,f(x_i;\theta_{ctr})×f(x_i;\theta_{cvr})) \notag \end{align}\]

可以将模型利用的样本视为 (show, click, convert) pair 对，则相比传统 cvr 模型，ESMM 能够利用那些曝光未点击的样本 (即下表中最后一列，0/1 表示对应的中间链路事件是否发生)

showclickconvert
111
110
100

在预估时，通过如下条件概率公式，能够从统计意义上保证 cvr 的值是无偏的

\[\begin{align} p(z=1|y=1,x) = \frac{p(y=1,z=1|x)}{p(y=1|x)} \end{align}\]

实验效果如下，各种方法的具体含义如下

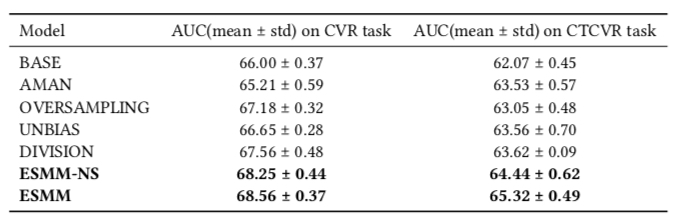
ESMM 效果对比
  • BASE: 普通建模 CVR 模型
  • AMAN: 对负样本做 negative sampling
  • OVERSAMPLING: 对正样本做 over sampling
  • UNBIAS: 参考 这篇 paper 将 pCTR 当做 rejection probability
  • DIVISION: 分别建模 pCTR 和 pCTCVR，然后利用上面的公式计算 pCVR
  • ESMM-NS: 不 share bottom 的 ESMM
  • ESMM: share bottom 的 ESMM

IPS(Inverse Propensity Score)

Inverse Propensity Score 的做法是为每个有 label 的样本预估一个 propensity score (倾向性得分)，其含义直观来说就是样本进入训练集 (被标记 label) 的概率，如对于 CTR 模型，propensity 就是曝光的概率，对于 CVR 模型，propensity 就是点击的概率

IPS 实际上借鉴了 Importance Sampling 的思想，通过给每个样本一个概率值作为权重，从统计学上证明了基于观测到的数据求得的期望与全量数据的期望是一致，其推导过程可简单描述为如下方式

记 \(L\) 是观测到 label 的样本数，\(L'\) 则是同时包含了那些没被观测到的样本 (\(L' \gg L\)); 则无偏的优化目标应该是 (\(y_i\)、\(p_i\) 分别表示 label 与预估值)

\[\begin{align} \min \sum_{i=1}^{L'} l(y_i, p_i) \tag{1} \end{align}\]

现在令第 \(i\) 个样本的是否被观测到记为 \(O_i \in \lbrace 0, 1 \rbrace\)，则可假设 \(O_i\) 服从一个伯努利分布即 \(O_i \sim Bern(z_i)\), 这里的 \(z_i\) 是样本 \(i\) 被观测到的概率，则上面的优化问题可写成如下形式

\[\begin{align} Loss &= \sum_{i=1}^{L'} l(y_i, p_i)\notag \\\ &= \sum_{i=1}^{L'} \frac{l(y_i, p_i)}{z_i} E_{O}(O_i)\notag \\\ &= E_{O}(\sum_{i=1}^{L'} \frac{l(y_i, p_i)}{z_i} O_i)\notag \\\ &= \sum_{i=1}^{L} \frac{l(y_i, p_i)}{z_i}\notag \end{align}\]

则上面问题 (1) 可被写成如下形式， 即可通过观测到的数据进行模型的训练，而 \(z_i\) 可利用 label 为是否被观测到的数据进行训练，训练方式可以是单独训练或与这个 task 做 joint training。

\[\begin{align} \min \sum_{i=1}^{L} \frac{l(y_i, p_i)}{z_i} \tag{2} \end{align}\]

而如果套用 importance sampling 的方法，其实也能得到上面问题 (2) 的形式，在观测到的样本中， 样本 \(i\) 被采样的概率是 \(z_i\), 而在全部样本中，由于每个样本都会被采样到，因此其采样概率是 1，即加权的系数是 \(\frac{1}{z_i}\)

此外，也有方法同时融合了第一类方法中的 imputation model 和这里的 IPS 方法，被称为 Doubly Robust Method，则其损失函数可写成如下形式（\(\sigma_i\) 是通过 imputation model 得到的 label）

\[\begin{align} \min \sum_{i=1}^{L} (\frac{l(y_i, p_i)}{z_i} - l(\sigma_i, p_i)) + \sum_{i=1}^{L'} l(\sigma_i, p_i) \end{align}\]

上述方法在 Improving Ad Click Prediction by Considering Non-displayed Events 有较为详细的描述，可以参考一下

Domain Adaption

Domain Adatption 可以认为是 transfer learning 的一个子领域，根据 wiki 的说法其目标是

aim at learning from a source data distribution a well performing model on a different (but related) target data distribution.

这个说法比较宽泛，实际中用到的方法可分为下面四大类 (from wiki)，实际上跟我们上面提到的方法的思想都比较相似

  1. Reweighting algorithms: reweight the source labeled sample such that it "looks like" the target sample (in terms of the error measure considered).
  2. Iterative algorithms：iteratively "auto-labeling" the target examples
  3. Search of a common representation space：construct a common representation space for the two domains
  4. Hierarchical Bayesian Model：build a factorization model to derive domain-dependent latent representations allowing both domain-specific and globally shared latent factors

而在 Exposure Bias 场景下，观测到的数据被当做 source domain，全量数据被当做 target domain，利用 domain adaption 解决 exposure bias 比较有代表性的 paper 是阿里在 2020 发表的 ESAM，ESAM: Discriminative gDomain Adaptation with Non-Displayed Items to Improve Long-Tail Performance

ESAM (Entire Space Adaption Modelling) 跟上面提到的 ESMM (Entire Space Multi-Task Model) 名字很相似，要解决的问题也很相似，但是前者是召回场景， 后者是 cvr 场景；

ESAM 总体如下所示，各符号含义如下（基本上就是向量化召回的涉及到的概念）

  • \(q\): query
  • \(d^s\): 有曝光的 item
  • \(d^t\): 没有曝光的 item
  • \(f_q\), \(f_d\): 将 query 和 item 映射成 embedding 的函数
  • \(v_{q}\), \(v_{d}\): query 和 item 被 \(f_q\), \(f_d\) 映射出来的 embedding
  • \(f_s\): 计算 \(v_{q}\), \(v_{d}\) 相似性的函数，常见的是內积
  • \(L_s\): 基于 \(f_s\) 吐出的预估值 \(S_{c_{q,d^s}}\) 计算的损失函数，常见的有 point-wise、pair-wise、list-wise 三大类
  • \(L_{DA}\)、\(L_{DC}^{c}\)、\(L_{DC}^{p}\): paper 中提出的缓解 exposure bias 的三种途径，以 loss 形式叠加在原始的 \(L_s\) 上，也是下文要重点展开描述的部分
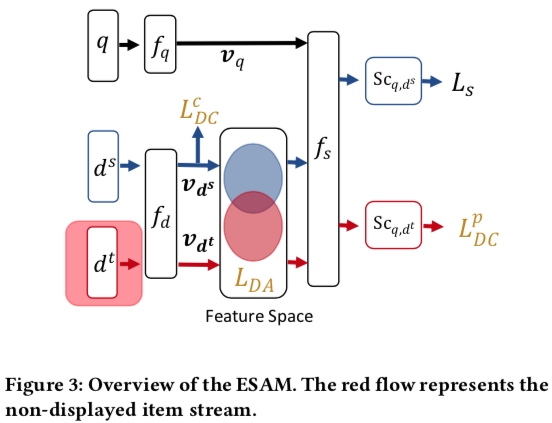
ESAMOverview

ESAM 的核心在于叠加在原始损失函数 \(L_s\) 上的三项：\(L_{DA}\)、\(L_{DC}^{c}\)、\(L_{DC}^{p}\)，下面会分别描述这三项的含义和计算方式

\(L_{DA}\)：Domain Adaptation with Attribute Correlation Alignment

这个 loss 项的出发点是两个特征在 source domain 和 target domain 中的相关性是保持一致的，如下图所示，左边的图认为 price 跟 brand 是具有强相关的、brand 跟 material 中度相关、price 跟 material 弱相关，而 \(L_{DA}\) 这个损失项是基于下面两个假设产生的

  1. 相关性在 source domain 和 target domain 都是一致的
  2. 原始的特征 (即 price、brand、material) 会被映射到 embedding 中某一维或几维
L_DA

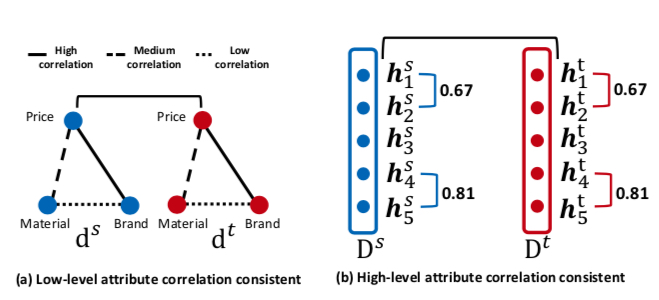
因此，可以设计 loss 项令两个特征的相关性在 source domain 和 target domain 尽可能保持一致 , 而这里的相关性可采用协方差

因此，\(L_DA\) 项计算方式如下，令 \(D^{s} = \lbrack v_{d_1^s};v_{d_2^s};\dots v_{d_n^s} \rbrack \in \mathbb{R}^{n×L}\) 为 n 个 source domain 样本映射出来的 embedding matrix，而 \(D^{s} = \lbrack v_{d_1^t};v_{d_2^t};\dots v_{d_n^t} \rbrack \in \mathbb{R}^{n×L}\) 则是 n 个 target domain 样本映射出来的 embedding matrix, 每个 \(v\) 是一个长度为 \(L\) 的向量

如果将每个 embedding 相同的维度提取出来作为一个 vector \(h\)，则 \(D^{s}\) 和 \(D^{t}\) 也可写成如下形式，每个 \(h\) 是一个长度为 \(n\) 的向量

\(D^{s}=\lbrack h_{1}^{s},h_{2}^{s};\dots h_{L}^{s} \rbrack \in \mathbb{R}^{n×L}\)
\(D^{t}=\lbrack h_{1}^{t},h_{2}^{t};\dots h_{L}^{t} \rbrack \in \mathbb{R}^{n×L}\)

则 \(L_{DA}\) 计算方式如下

\[\begin{align} L_{DA} &= \frac{1}{L^2}\sum_{(j,k)}({h_j^s}^T{h_k^s} - {h_j^t}^T{h_k^t})^2 \notag \\\ &= \frac{1}{L^2} ||Cov(D^s) - Cov(D^t)||_F^2 \notag \end{align}\]

上式中的 \(Cov(D^s) \in \mathbb{R}^{L×L}\) 和 \(Cov(D^t) \in \mathbb{R}^{L×L}\) 分别代表 source domain 和 target domain 的 covariance matrix，此外，笔者认为上面的公式其实表达不完全准确，因为 covariance 计算还需要减去均值的，上面并没有这么做

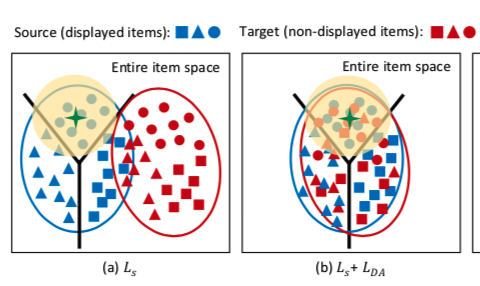
加上改了这一项后，可以认为 source domain 和 target domain 在向量空间中的分布变化如下

ESAM_L1

\(L_{DC}^{c}\)：Center-Wise Clustering for Source Clustering.

第二项 loss \(L_{DC}^{c}\) \(L_{DC}^{c}\) 跟人脸识别中最早提出的 center loss 很相似，就是让相同类型的样本在向量空间中尽可能接近，在广告的场景下这个类型可以是 click、non-click、purchase 等；此外，还会令不同类型的样本在向量空间中的距离尽可能远；这个思想比较好理解

而为了定义出距离，会为每一个类型定义出一个聚类中心，聚类中心会被参数化；具体计算方式如下

\[\begin{align} L_{DC}^{c} &= \sum_{j=1}^{n} \max(0, ||\frac{v_{d_j^s}}{||v_{d_j^s}||} - c_{q}^{y_j^s}||_{2}^{2} - m_1) \notag \\\ &+ \sum_{k=1}^{n_y} \sum_{u=k+1}^{n_y} \max(0, m2 - ||c_{q}^{k} - c_{q}^{u}||_{2}^{2})\notag \end{align}\]

上面的公式中 \(m_1\) 和 \(m_2\) 分别是两个 margin，表示样本距离其类簇距离小于 \(m_1\) 和 类簇之间的距离大于 \(m_2\) 的情况下无需优化；同时假设所有样本有 \(n_y\) 种类型，第 \(k\) 种类型 (即样本 label 为 \(Y_k\)) 样本的 center 是 \(c_{q}^{k}\)，其定义为当前训练样本中类型为 \(k\) 的样本的向量的中心，表示如下 (\(\delta(cond)\) 函数的值为 1 (cond=true) 或 0 (cond=false))

\[\begin{align} c_q^k = \frac{\sum_{j=1}^{n} \delta(y_j^s = Y_k)\frac{v_{d_j^s}}{||v_{d_j^s}||}}{\sum_{j=1}^{n} \delta(y_j^s = Y_k)} \end{align}\]

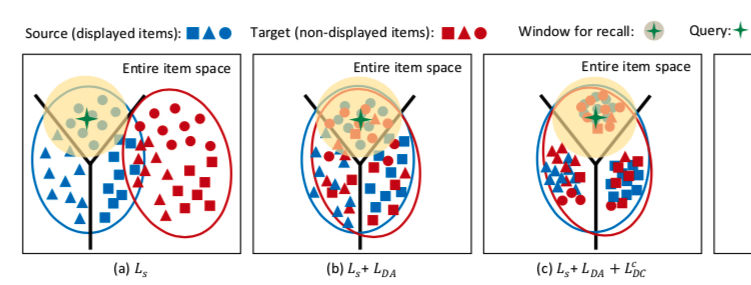
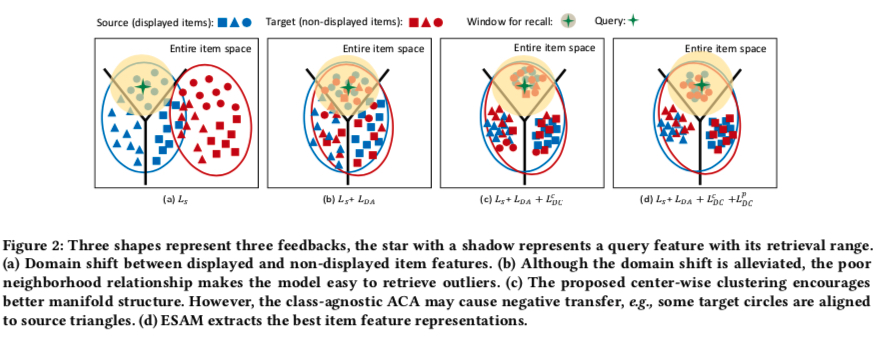
则加入 \(L_{DC}^{c}\) 这一项后，source domain 和 target domain 在向量空间中的分布变化如下，可以看到，虽然 target domain 中的样本具有高内聚性，但是其聚类的簇可能是错误，其原因是对于 target domain 中的样本，目前为止都没有加入 label 信息，而这便是下一项 loss \(L_{DC}^{p}\) 要解决的问题

ESAM_Loss2

\(L_{DC}^{p}\)：Self-Training for Target Clustering.

从这项 loss 的描述中的 self training，可以猜测其做法是为 target domain 中 unlabeled 的样本打上标签用于训练模型，这是 semi supervised learning 中常见做法，而 paper 中并没有直接为 unlabeled 的样本打上标签，而是通过 loss \(L_{DC}^{p}\) 较为巧妙地实现了这一点，其表达如下

\[\begin{align} L_{DC}^{p} = -\frac{\sum_{j=1}^{n} \delta(S_{c_{q,d^t}} < p_1 | S_{c_{q,d^t}} > p_2)S_{c_{q,d^t}} \log S_{c_{q,d^t}}} {\sum_{j=1}^{n} \delta(S_{c_{q,d^t}} < p_1 | S_{c_{q,d^t}} > p_2)} \end{align}\]

其中 \(p_1\) 和 \(p_2\) 是两个阈值，表示含义是样本的置信度达到一定程度才认为其是负样本 / 正样本，则这个 loss 的目标会让预估值小于 \(p_1\) 的样本预估值更接近 0，预估值大于 \(p_2\) 的样本的预估值更接近 1，原因见可以看下面画出的 \(-p(x) \log p(x)\) 的函数，直接令这一项最小即可达到 self-training 的目标

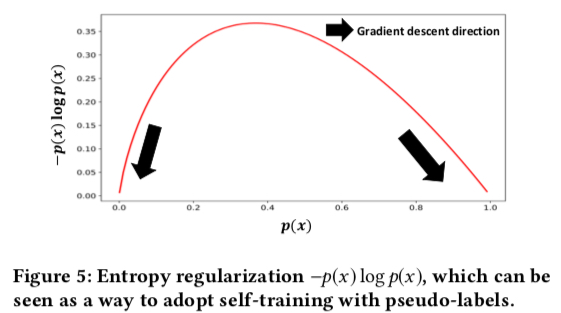
Entropy regularization

加入 \(L_{DC}^{p}\) 这一项后，source domain 和 target domain 在向量空间中的分布变化如下，也是 ESAM 的最终形态

ESAM_Loss3

则最终的 loss 为下式所示，其中 \(\lambda_1\), \(\lambda_2\), \(\lambda_3\) 是三个超参，通过 gradient descent 即可求解

\[\begin{align} L_{all} = L_s + \lambda_1 L_{DA} + \lambda_2 L_{DC}^{c} + \lambda_3 L_{DC}^{p} \end{align}\]

Summary

综上，本文主要针对 exposure bias 介绍了三大类方法，分别是 Data Augmentation、IPS 和 Domain Adaption，三类方法主要思想如下

  1. Data Augmentation: 即利用那些 unlabeled 的样本，方法较多，如将所有样本都当做负样本、训练一个 imputation model 来给 unlabeled 的样本打上标签、通过 multitask 方式利用等
  2. IPS：只利用曝光的样本，从概率论推导出给曝光样本进行合适的加权后，基于曝光的样本求的期望是无偏的
  3. Domain Adaption：利用了 unlabeled 的样本，主要分析了 ESAM 这篇 paper, 同时通过在 loss 上添加了三项，能够令曝光和未曝光的 item 训练得到的向量空间尽可能保持一致，这三项的 loss 背后的思想也值得参考

此外，上面的一些方法虽然从理论上看起来比较 fancy，但是根据笔者当前的工作经验，实际中应用这些方法，还需要考虑到模型的迭代效率、、理论的假设是否符合实际等等；比如说 data augmentation/ESAM 方法会导致数据量增加不止一个量级，而这会势必会导致训练时长增加，即使这个方法有效果，也要考虑带来的收益以及牺牲的迭代效率和机器资源等兑换是否划算， 或者考虑如何改进采样策略尽可能打平样本量。