《Programming Collective Intelligence》读书笔记 (2)-- 协同过滤
《Programming Collective Intelligence》(中文名为《集体智慧编程》),是一本关于数据挖掘的书籍,每一章都会通过一个实际的例子来讲述某个机器学习算法,同时会涉及到数据的采集和处理等,是一本实践性很强的书籍。
本文是关于本书的第二章 Making Recommendations 的前半部分。主要讲述了寻找用户相似性和物品相似性的方法,并在这个基础上讲述如何为用户推荐物品。
推荐这个功能在很多网站或软件都有实现,如淘宝,当当,网易云音乐等。实现推荐的算法也许有很多。本文主要讲的是协同过滤。
下面分为这几部分来讲述:
1. 寻找用户相似性的几种方法
2. 基于用户相似性为用户推荐物品
3. 寻找物品相似性的方法
在讲述之前假定一下的数据集:1
2
3
4
5
6
7
8
9
10# 电影评分数据集,用于后面的的测试
# critics 字典里面每一项是一个用户对若干部电影的评分
critics={'Lisa Rose': {'Lady in the Water': 2.5, 'Snakes on a Plane': 3.5,'Just My Luck': 3.0, 'Superman Returns': 3.5, 'You, Me and Dupree': 2.5,'The Night Listener': 3.0},
'Gene Seymour': {'Lady in the Water': 3.0, 'Snakes on a Plane': 3.5,'Just My Luck': 1.5, 'Superman Returns': 5.0, 'The Night Listener': 3.0,'You, Me and Dupree': 3.5},
'Michael Phillips': {'Lady in the Water': 2.5, 'Snakes on a Plane': 3.0,'Superman Returns': 3.5, 'The Night Listener': 4.0},
'Claudia Puig': {'Snakes on a Plane': 3.5, 'Just My Luck': 3.0,
'The Night Listener': 4.5, 'Superman Returns': 4.0,'You, Me and Dupree': 2.5},
'Mick LaSalle': {'Lady in the Water': 3.0, 'Snakes on a Plane': 4.0,'Just My Luck': 2.0, 'Superman Returns': 3.0, 'The Night Listener': 3.0,'You, Me and Dupree': 2.0},
'Jack Matthews': {'Lady in the Water': 3.0, 'Snakes on a Plane': 4.0,'The Night Listener': 3.0, 'Superman Returns': 5.0, 'You, Me and Dupree': 3.5},
'Toby': {'Snakes on a Plane': 4.5, 'You, Me and Dupree': 1.0,'Superman Returns': 4.0}}
寻找用户相似性的几种方法
欧几里得距离
基于上面的数据集,最容易想到的第一种方法就是衡量他们所评的分数的距离。这个怎么理解呢?比如说 A 对两部电影的评分是 1 和 2,B 对两部电影的评分书 3 和 4。那么他们评分的距离就是 \(\sqrt{(1-3)^2+(2-4)^2 }\)。如果有多部电影则以此类推。这相当与把一个用户所有评分用多维空间中的一个点来表示,用户间的相似性用点间的距离来衡量,距离越小,相似度越高。原文称这种距离为欧几里得距离分数(Euclidean Distance score)。
通过 python 实现也很简单:1
2
3
4
5
6
7
8
9# 通过欧几里得距离找用户相似性,为了使返回数值越大,表示相似性越高,对得出的距离取倒数即可,范围为(0,1)
import math
def similarUserWithEuclidean(scores,user1,user2):
commom = [movie for movie in scores[user1] if movie in scores[user2]]
if len(commom) == 0: #没有相同喜爱的电影
return 0
total = sum([math.pow(scores[user1][movie] - scores[user2][movie], 2) for movie in commom])
similarity=math.sqrt(total)
return 1/(total+1)
上面实现的方法虽然简单,但是存在着分数膨胀 (grade inflation) 的问题,比如说 A 和 B 两个人的评判标准不一样,A 比较苛刻,给三部电影打的分数是 1、2、1,但是 B 要求不会那么高,给两部电影打分为 4、5、4,如果用第一种方法那他们在二维空间中的距离将会比较大,从而被判为无相似性。那么他们真的是没有相似性吗?
虽然他们在分数值上存在区别,但是两个人在每部电影的评分差上保持一致性,也可认为他们是相似用户。因为在对于好和不好的标准上每个人都会有自己的度量,也许对于 A 来说 2 就算是好的了,但是对于 B 来说好的标准是 5。假如对于多部电影两者的评分趋势一致,那么可认为两者的品味也是差不多的,可以认为他们有相似性。通过皮尔逊相关系数(Pearson Correlation Coefficient)可以实现上面的功能。
皮尔逊相关系数
皮尔逊相关系数取值范围为 [-1,1], 数值为正表示正相关,且越大表示相关性越强;数值为负则为负相关,越小则负相关性越强。计算公式如下:
\[\begin{align} sim = \frac{\sum_{c \in I_{ij}}(R_{i,c} - \overline{R_i})(R_{j,c} - \overline{R_j})}{\sqrt{\sum_{c \in I_{ij}} (R_{i,c} - \overline{R_i})^2} \sqrt{\sum_{c \in I_{ij}} (R_{j,c} - \overline{R_j})^2} } \end{align}\]
公式中的符号意义如下:
| 符号 | 含义 |
|---|---|
| \(I_{ij}\) | 用户 \(i\) 和用户 \(j\) 的公共评分集,也就是两者都有评分的物品的集合 |
| \(R_{i,c}\) | 用户 \(i\) 对物品 c 的评分 |
| \(R_{j,c}\) | 用户 \(j\) 对物品 c 的评分 |
| \(\overline {R_i}\) | 用户 \(i\) 对 \(I_{ij}\) 中物品评分的均值 |
| \(\overline {R_j}\) | 用户 \(j\) 对 \(I_{ij}\) 中物品评分的均值 |
皮尔逊系数的公式初看有点长,但是如果对概率论了解的同学可知,对于变量 \(X\) 和 \(Y\) ,上面的皮尔逊系数的表达式其实就是 \[\frac {X 和 Y 的协方差}{X 的标准差 \*Y 的标准差}\],而这就是概率论中对相关系数的定义。实际上概率论中的相关系数就是皮尔逊提出的这个皮尔逊相关系数率 (这里需要注意的是,对于不同测量尺度的变数,有不同的相关系数可用,而我们接触到的概率论教材里,大多是都是讲皮尔逊相关系数,实际上还有其他的相关系数)。
用图像直观表示皮尔逊相关系数如下所示,假设 r 为互相关系数:
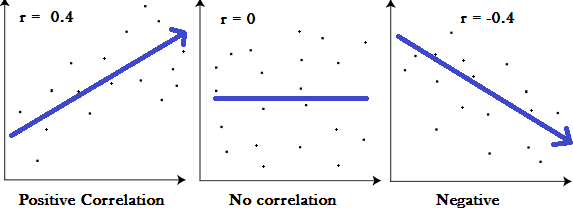
且一般认为 r 值范围和相关性的对应关系如下,0 表示两者无关:
| 相关性强弱 | 对应的 r 值 |
|---|---|
| High correlation | 0.5~1.0 or -0.5~ -1.0 |
| Medium correlation | 0.3 ~ 0.5 or -0.3~ -0.5 |
| Low correlation | 0.1~0.3 or -0.1~ -0.3 |
关于皮尔逊系数更详细的资料可参考该链接:http://www.statisticshowto.com/what-is-the-pearson-correlation-coefficient
实现该功能的代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15# 通过 Pearson Correlation Coefficient 计算两个用户的相似性,数值绝对值越大相关性,正负表示正相关或负相关
def similarUserWithPearson(scores,user1,user2):
commom = [movie for movie in scores[user1] if movie in scores[user2]]
if len(commom) == 0: #no common item of the two users
return 0
average1 = float(sum(scores[user1][movie] for movie in scores[user1]))/len(scores[user1])
average2 = float(sum(scores[user2][movie] for movie in scores[user2]))/len(scores[user2])
# denominator
multiply_sum = sum( (scores[user1][movie]-average1) * (scores[user2][movie]-average2) for movie in commom )
# member
pow_sum_1 = sum( math.pow(scores[user1][movie]-average1, 2) for movie in commom )
pow_sum_2 = sum( math.pow(scores[user2][movie]-average2, 2) for movie in commom )
modified_cosine_similarity = float(multiply_sum)/math.sqrt(pow_sum_1*pow_sum_2)
return modified_cosine_similarity
上面两种方法是书中提到的,并且计算皮尔逊相关系数的方法与原书有区别,但是结果是一样的。只是原书上对公式进行了进一步的简化。除此之外,还有一类比较常用的方法是通过余弦相似性(Cosine Similarity)判断用户相似性。原理也是用空间中的一个多维向量表示用户对所有电影的评分,用户间的相似性可以通过向量间的夹角表示,取值范围也是(-1,1)。但是因为这种方法也存在上面提到的分数膨胀 (grade inflation),在此基础上提出了修正的余弦相似度(Adjusted Cosine Similarity)。
修正的余弦相似性
修正的余弦相似度跟上面提到的皮尔逊系数很相似,包括计算公式,区别在于皮尔逊系数是依据双方共同评分项进行计算,而修正的余弦相似度则对所有项都进行运算。比如说一部电影 A 有评分,B 没有评分,那么计算皮尔逊系数时就不能采用这不电影作为计算的数据集,但是计算修正的余弦相似性则可以利用这个数据。
修正的余弦相似性的计算公式如下
\[\begin{align} sim = \frac{\sum_{c \in I_{ij}}(R_{i,c} - \overline{R_i})(R_{j,c} - \overline{R_j})}{\sqrt{\sum_{c \in I_i} (R_{i,c} - \overline{R_i})^2} \sqrt{\sum_{c \in I_j} (R_{j,c} - \overline{R_j})^2} } \end{align}\]
公式中的符号意义如下:
| 符号 | 含义 |
|---|---|
| \(I_{ij}\) | 用户 \(i\) 和用户 \(j\) 的公共评分集,也就是均被两者评分的物品的集合 |
| \(I_i\) | 被用户 \(i\) 评分了的物品的集合 |
| \(I_j\) | 被用户 \(j\) 评分了的物品的集合 |
| \(R_{i,c}\) | 用户 \(i\) 对物品 c 的评分 |
| \(R_{j,c}\) | 用户 \(j\) 对物品 c 的评分 |
| \(\overline {R_i}\) | 用户 \(i\) 所有评分的均值 |
| \(\overline {R_j}\) | 用户 \(j\) 所有评分的均值 |
这条公式跟上面的皮尔逊相关系数很相似,皮尔逊相关系数的公式如下:
\[\begin{align} sim = \frac{\sum_{c \in I_{ij}}(R_{i,c} - \overline{R_i})(R_{j,c} - \overline{R_j})}{\sqrt{\sum_{c \in I_{ij}} (R_{i,c} - \overline{R_i})^2} \sqrt{\sum_{c \in I_{ij}} (R_{j,c} - \overline{R_j})^2} } \end{align}\]
两者的区别在于分母上,皮尔逊系数的分母采用的评分集是两个用户的共同评分集(就是两个用户都对这个物品有评价),而修正的余弦系数则采用两个用户各自的评分集。
采用修正的余弦系数的实现代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14def user_similarity_on_modified_cosine(scores, user1, user2):
commom = [movie for movie in scores[user1] if movie in scores[user2]]
if len(commom) == 0: #no common item of the two users
return 0
average1 = float(sum(scores[user1][movie] for movie in scores[user1]))/len(scores[user1])
average2 = float(sum(scores[user2][movie] for movie in scores[user2]))/len(scores[user2])
# denominator
multiply_sum = sum( (scores[user1][movie]-average1) * (scores[user2][movie]-average2) for movie in commom )
# member
pow_sum_1 = sum( math.pow(scores[user1][movie]-average1, 2) for movie in scores[user1] )
pow_sum_2 = sum( math.pow(scores[user2][movie]-average2, 2) for movie in scores[user2] )
modified_cosine_similarity = float(multiply_sum)/math.sqrt(pow_sum_1*pow_sum_2)
return modified_cosine_similarity
计算最相似的前 n 个用户
通过上面任意一种方法找出用户相似度后,可以根据相似度的大小排序,找出前 n 个最相似的用户,实现代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37def findSimilarUsers(scores,user,similarFunction = similarUserWithPearson):
similarUser = [(similarFunction(critics, user, otherUser), otherUser) for otherUser in scores if otherUser!=user]
# 使用了dict会将含有kv对的列表封装成一个字典,无法利用列表自带的排序函数sort
# similarDict = dict([(similarFunction(user,otherUser),otherUser) for otherUser in scores if otherUser!=user])
similarUser.sort()
similarUser.reverse()
#也可将上面两行改成:similarUser.sort(reverse = True)
return similarUser # 返回相似度从高到低排序的一个列表
```
### 小结
传统的计算相似度的方法就是上面提到的三种:**余弦相似度、修正的余弦相似度和相关相似性(也就是计算皮尔逊系数)**。下面是分别采用上面三种方法为测试数据集中的用户`Lisa Rose`找到前6个最相似用户的结果。完整的代码见文末
```
# 欧几里得距离,第一个值是分数,第二个值是具体的用户
(0.4444444444444444, 'Michael Phillips')
(0.3333333333333333, 'Mick LaSalle')
(0.2857142857142857, 'Claudia Puig')
(0.2222222222222222, 'Toby')
(0.21052631578947367, 'Jack Matthews')
(0.14814814814814814, 'Gene Seymour')
# 皮尔逊系数,第一个值是分数,第二个值是具体的用户
(0.9345507010964664, 'Toby')
(0.747017880833996, 'Jack Matthews')
(0.5940885257860046, 'Mick LaSalle')
(0.5477225575051661, 'Claudia Puig')
(0.39605901719066977, 'Gene Seymour')
(0.3872983346207417, 'Michael Phillips')
# 修正的余弦相似度,第一个值是分数,第二个值是具体的用户
(0.8093446482740976, 'Toby')
(0.747017880833996, 'Jack Matthews')
(0.5940885257860046, 'Mick LaSalle')
(0.4743416490252569, 'Claudia Puig')
(0.39605901719066977, 'Gene Seymour')
(0.33541019662496846, 'Michael Phillips')
从结果可以看到,修正的余弦相似度和皮尔逊系数大小虽然不一样,但是预测的整体用户相似度分布一致。
为用户推荐物品
经过第一步找出相似用户后,可以直接对相似用户之间进行物品推荐,如 A 和 B 相似,且 B 有部分喜欢的电影 A 没看过,就可以为 A 推荐这部分电影。
为了使得推荐结果更具有代表性,需要考虑多几位相似用户,同时也是为了有更多可推荐的选择,因为可能 B 看过而 A 没看过的电影也不多。
实现思路如下:为 A 找出了若干位相似用户,每个用户都有一个相似度系数(就是上面的皮尔森系数),找出他们看过而 A 没看过电影集合 T。将每个用户的相似度乘上用户对集合 T 中某部电影的评分便可作为这部电影的得分,得分越高,代表推荐性越强。这乍一看还比较合理。但是一分析也存在一个问题,就是假如一部电影实际上都符合这一批用户的,但是看过的人很少,其他一些不太符合的电影因为看过的人多而的得分高。这就导致了误判。怎么解决呢?
这里需要引入一个因子来调和这种不平衡性,使得结果能够合理,既然这种不平衡是由于评分的人数不同而引起的,那么就可以从这里着手。将上面相加得到的总分除以对这部电影有评分的所有用户的相似性。
例如下图就是为上面 Toby 推荐的结果:
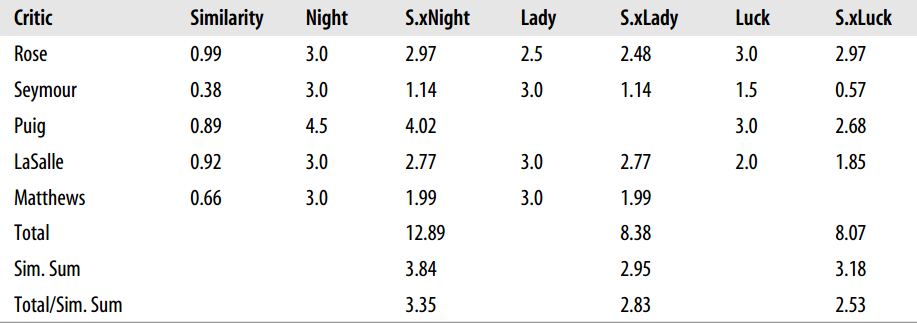
实现的代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27# 给用户推荐物品,物品的评分采用与其他用户的相似度乘上其他用户的实际评分
def recommendItem(scores,user):
userSimilarity = findSimilarUsers(scores, user)
swapUserSimilarity = {v:k for k, v in userSimilarity} # 交换键值,将存储kv对的列表转换为字典,交换后为无序
allMovies = []
for (k,v) in critics.items():
for movie in v:
if movie not in allMovies:
allMovies.append(movie)
itemScore = []
for movie in allMovies:
scoreSum = 0
similaritySum = 0
for similarity, otherUser in userSimilarity:
if critics[otherUser].has_key(movie):
scoreSum += critics[otherUser][movie] * similarity
similaritySum += swapUserSimilarity[otherUser]
itemScore.append((scoreSum/similaritySum, movie))
itemScore.sort(reverse=True)
recommend_movies = [] # 为user推荐的电影
print 'all movies ranking:'
for i,j in itemScore:
print i,j
if j not in critics[user]:
recommend_movies.append(j)
print 'recommended movies for %s:%s' %(user, recommend_movies)
寻找物品间的相似性
上面的推荐方法是通过寻找相似用户进行推荐,是一种 “A 喜欢这个物品,跟他相似的 B 也可能喜欢这件物品” 思想;除此之外,还有一种思想就是 “A 喜欢物品 1,也可能喜欢相似的物品 2”。在这里判断 1 和 2 的相似性就成了关键,也就是如何寻找物品间的相似性。
乍一看会没有思路,但是实际上很简单,只需要对原始数据做个简单的转换。上面一开始给出的数据集是一个用户对多部电影的评价,现在把换成同一部电影不同用户的评价即可.1
2
3
4
5
6将
'Lisa Rose': {'Lady in the Water': 2.5, 'Snakes on a Plane': 3.5},
'Gene Seymour': {'Lady in the Water': 3.0, 'Snakes on a Plane': 3.5}}
转换为
{'Lady in the Water':{'Lisa Rose':2.5,'Gene Seymour':3.0},
'Snakes on a Plane':{'Lisa Rose':3.5,'Gene Seymour':3.5}} etc..
这样上面求用户相似性的方法是不是同样可以用来求物品间的相似性了?这种基于物品相似性的方法称为基于物品的协同过滤,而上面基于用户相似性的方法则称为基于用户的协同过滤。
文中完整代码见这里
文章为笔者总结,如有错误,烦请指出