LeetCode 解题报告 (207,210)-- 拓扑排序 (Topological Sort)
拓扑排序是有向图中一种较常用的排序方法,本文主要以 LeetCode 上的两道题目 207. Course Schedule 和 210. Course Schedule II 讲述如何拓扑排序的概念与使用方法。
LeetCode 上的两道题目是关于拓扑排序(Topological Sort)比较经典的两道题目,大意就是有 0~(n-1) 的 n 门课程需要修,但是有部分课程需要先修了别的课程才能修,问是否能修完所有课程。从题意可知,将这些课程及依赖关系表示成一个有向图,那么当图中存在闭环时是不可能修完所有课程的,因为形成闭环的几门课程相互依赖,无法选择第一门开始修的课程。
因此题目就是要求判断一个有向图中是否存在闭环。
最直观的思路就是通过深度优先搜索以每个点为起点遍历,判断每次的遍历中是否存在闭环,若存在则无法修完,反之则可以。
针对 207. Course Schedule,利用上面的思路实现的代码如下所示1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28class Solution(object):
def canFinish(self, numCourses, prerequisites):
"""
:type numCourses: int
:type prerequisites: List[List[int]]
:rtype: bool
"""
course = [[0 for i in xrange(numCourses)] for j in xrange(numCourses)]
for s in prerequisites:
course[s[0]][s[1]] = 1
visited = [0 for i in xrange(numCourses)]
for i in xrange(numCourses):
if self.dfs(course, i, visited)==False:
return False
return True
def dfs(self, course, num, visited):
for i in xrange(len(course[num])):
if course[num][i] == 1:
visited[num] = 1
if visited[i] == 1:
return False
else:
if self.dfs(course, i, visited) == False:
return False
visited[num] = 0
这个方法的时间复杂度是 \(O(n^2)\),n 是图中所有点的数目。在提交时会提示 TLE。
其实解决这种问题还有更好的方法,就是下面要介绍的拓扑排序,拓扑排序实际上返回的结果是有向图中所有点依据有向边指向顺序的排列而成的点。下面是拓扑排序的两个例子,第一个是合法的拓扑排序的结果,第二个是非法的拓扑排序结果。
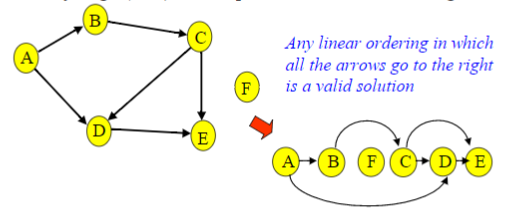
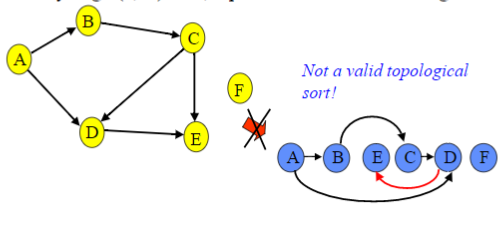
那么该如何获得一个有向图的拓扑排序的结果?
最直观的方法步骤如下 (1) 找到图中入度(indegree)为 0 的点,然后记录这个点并删除这个点的所有出度(outdegree),也就是连接了这个点的其他点的入度 (2) 检查图中是否有入度为 0 的点,如果有重复步骤(1)
重复步骤(1)-(2)直至无法找到入度为 0 的点,此时如果记录的点的数目与所有点的数目相同,那么说明图中不存在闭合的环,反之则存在。
上面这种方法虽然比较直观,但是每次找到入度为 0 的点的时间复杂度是 \(O(n)\), 因此总的时间复杂度是 \(O(n^2)\),n 为图中所有点的数目。下面介绍一种利用队列将时间复杂度降为 \(O(n+e)\),e 为图中所有边的数目。
这种方法特殊的地方在于利用了一个队列存储当前入度为 0 的点,每次队首元素出列时,将队首元素出度相连的所有点的入度减去 1。因此还需要一个额外的空间存储每个点出度连接的所有点。整体的数据结构如下:
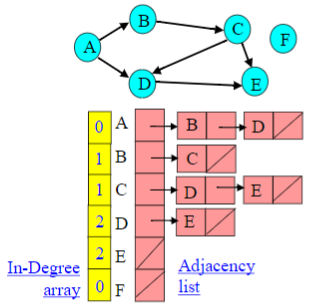
图中的 In-Degree array 就是存储每个点的入度数的队列,而 Adjacency list 则是存储每个点通过出度连接的所有点的数据结构。
这个算法的具体流程如下: (1) 遍历有向图中所有的边可以构造出上面提到的两个数据结构,时间复杂度为 \(O(e)\) (2) 从 In-Degree array 中找所有点中入度数为 0 的点,构成初始队列,时间复杂度 \(O(n)\) (3) 通过队首出列,调整与队首元素出度相连的所有点的入度数,并检查这些点的入度数是否为 0,若是则入队列 (4) 重复步骤 (3) 直至队列为空,此时若从队列中出列的所有点的数目为原来有向图中所有点的数目,则图中不存在闭合的环,且出列的顺序是一种可行的遍历方法。步骤 (3)(4) 的时间复杂度为 \(O(n+e)\)
因此这个方法的时间复杂度为 \(O(n+e)\), 除了能够判断有向图中是否有闭合的环,也能够给出一种合理的遍历方法,因此能解决上面提到的 207. Course Schedule 和 210. Course Schedule II两个问题。
下面是 207. Course Schedule 的解决方法1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27class Solution(object):
def canFinish(self, numCourses, prerequisites):
"""
:type numCourses: int
:type prerequisites: List[List[int]]
:rtype: bool
"""
indegree = [0 for i in xrange(numCourses)]
connection = {i:[] for i in xrange(numCourses)}
for link in prerequisites:
connection[link[1]].append(link[0])
indegree[link[0]] += 1
zero_indegree = []
for i in xrange(numCourses):
if indegree[i] == 0:
zero_indegree.append(i)
i = 0
while i<len(zero_indegree):
for node in connection[zero_indegree[i]]:
indegree[node] -= 1
if indegree[node] == 0:
zero_indegree.append(node)
i += 1
if len(zero_indegree) == numCourses:
return True
else:
return Falsereturn True 改为 return zero_indegree 即可。