Segment Tree 简介
简介
本文主要通过实际例子介绍 segment tree 这种数据结构及其应用。以 LeetCode 上的一道题目 307. Range Sum Query - Mutable 为例说明。
这道题目 307. Range Sum Query - Mutable要求求数组的区间和,但是有个额外条件,就是会进行多次数组区间求和以及数组元素的更新的操作。
从正常的思路出发,每次求和的时间复杂度为 \(O(n)\), 更新数组元素的时间复杂度为 \(O(1)\), 因此总体的时间复杂度为 \(O(n)\)。而参考 303. Range Sum Query - Immutable 可以实现求和的时间复杂度为 \(O(1)\), 但更新数组元素的时间复杂度为 \(O(n)\),所以总体的时间复杂度也是 \(O(n)\)。
上面两种方法的总体时间复杂度均为 \(O(n)\), 但是通过我们下面要介绍的 Segment Tree,能够将求和以及更新数组元素操作的时间复杂度均变为 \(O(log_2n)\)。
Segment Tree 是一棵二叉树,其特点为叶子节点个数与数组的长度相同 从左到右依次为数组中下标从小到大的元素的值,父节点的值为其左右的叶子节点的值的和。如下图是一个简单的例子
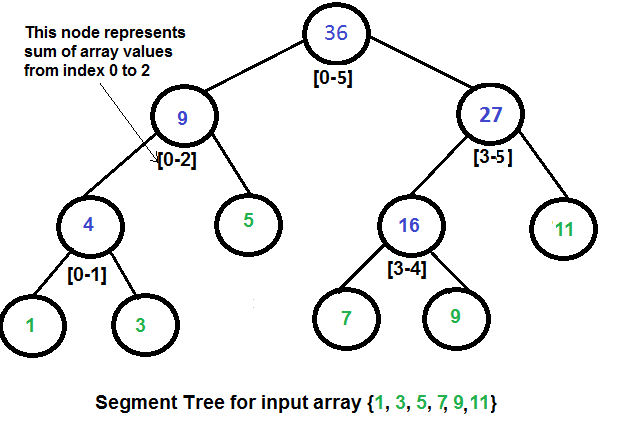
因此可以看到每个非叶子节点的值均是代表了数组某个区间的和。下面分别讲述如何构造这棵树,更新某个元素的值以及对特定区间求和。
建树
虽然逻辑上是一棵二叉树,但是实际存储时可以通过数组来实现,通过父子节点的下标的数值关系可以访问父节点的子节点。然后需要求出数组的大小,因为这是一棵满二叉树(full binary tree,具体定义见下),而且数组下标必须是连续的,因此需要的最大空间为 \({\displaystyle \sum _{k=0}^{m}2^k}\), 其中 m 为二叉树的高度 (从 0 开始计算,如上图的高度为 3)。
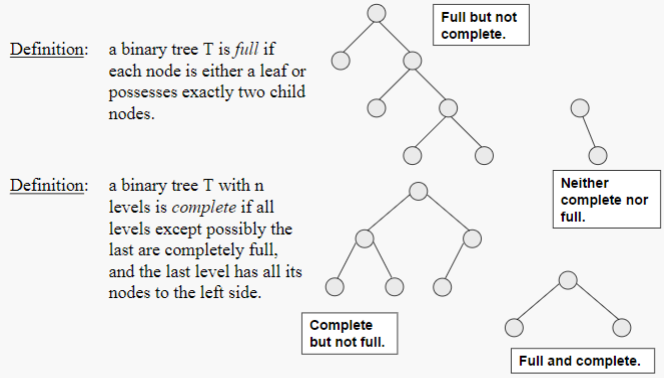
具体实现则通过递归,每次记录当前的节点的下标以及表示的数组的范围,如下为建树的 python 代码,其中 seg_tree 为建立的 segment tree,nums 为原数组,curr 为 segmen tree 中当前节点的下标,start、end 为以 curr 包含的 nums 数组的下标范围。1
2
3
4
5
6
7
8def build_tree(start, end, curr):
if start > end: return
if start == end:
seg_tree[curr] = nums[start]
else:
mid = start + (end - start)/2
seg_tree[curr] = build_tree(start, mid, curr*2+1) + build_tree(mid+1, end, curr*2+2)
return seg_tree[curr]
更新元素
更新元素需要更新两个地方,一是原数组对应的下标的值,另外一个是包含了这个元素的 segment tree 中的节点的值。具体也是通过递归实现,下面是更新 segment tree 中所有包含原数组下标为 idx 的元素的节点的值的 python 代码, diff 是下标为 idx 的新值与旧值之差。可见时间复杂度为 \(O(log_2n)\),n 为原数组元素的个数。1
2
3
4
5
6
7
8def update_sum( start, end, idx, curr, diff):
seg_tree[curr] += diff
if start == end: return
mid = start + (end - start)/2
if start <= idx <= mid:
update_sum(start, mid, idx, curr*2+1, diff)
else:
update_sum(mid+1, end, idx, curr*2+2, diff)
求区间和
求区间和也是通过递归实现,关键在于根据当前节点表示的范围以及需要求的区间的范围的关系进行求和。下面是实现的求区间 [qstart, qend] 的和的 python 代码。可见时间复杂度为 \(O(log_2n)\),n 为原数组元素的个数。1
2
3
4
5
6
7
8def get_sum(start, end, qstart, qend, curr):
mid = start + (end - start)/2
if qstart > end or qend < start:
return 0
elif start >= qstart and end <= qend:
return seg_tree[curr]
else:
return get_sum(start, mid, qstart, qend, curr*2+1) + get_sum(mid+1, end, qstart, qend, curr*2+2)
实际例子
下面结合上面讲述的三个步骤以及 LeetCode 上的题目 307. Range Sum Query - Mutable 给出完整的 AC 代码入下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58class NumArray(object):
def __init__(self, nums):
"""
initialize your data structure here.
:type nums: List[int]
"""
n = len(nums)
if n == 0: return
max_size = 2 * pow(2, int(math.ceil(math.log(n, 2)))) - 1
self.seg_tree = [0 for i in xrange(max_size)]
self.nums = nums[:]
self.build_tree(0, n-1, 0)
def build_tree(self, start, end, curr):
if start > end: return # empty list
if start == end:
self.seg_tree[curr] = self.nums[start]
else:
mid = start + (end - start)/2
self.seg_tree[curr] = self.build_tree(start, mid, curr*2+1) + self.build_tree(mid+1, end, curr*2+2)
return self.seg_tree[curr]
def update(self, i, val):
"""
:type i: int
:type val: int
:rtype: int
"""
diff = val - self.nums[i]
self.nums[i] = val
self.update_sum(0, len(self.nums)-1, i, 0, diff)
def update_sum(self, start, end, idx, curr, diff):
self.seg_tree[curr] += diff
if start == end: return
mid = start + (end - start)/2
if start <= idx <= mid:
self.update_sum(start, mid, idx, curr*2+1, diff)
else:
self.update_sum(mid+1, end, idx, curr*2+2, diff)
def sumRange(self, i, j):
"""
sum of elements nums[i..j], inclusive.
:type i: int
:type j: int
:rtype: int
"""
return self.get_sum(0, len(self.nums)-1, i, j, 0)
def get_sum(self, start, end, qstart, qend, curr):
mid = start + (end - start)/2
if qstart > end or qend < start:
return 0
elif start >= qstart and end <= qend:
return self.seg_tree[curr]
else:
return self.get_sum(start, mid, qstart, qend, curr*2+1) + self.get_sum(mid+1, end, qstart, qend, curr*2+2)