概率论与数理统计知识整理 (2)-- 二维随机变量的分布

发表于 2016-10-08 标签数学

前面讲到的随机变量都是一维的，但是某些试验中随机变量可能有多个，这里主要讨论二维的随机变量。

联合分布函数

假设 $X$ 和 $Y$ 都是随机变量，那么我们定义其分布函数如下：

\[\begin{align} F(x,y) = P ((X \le x)\cap(Y \le y)) = P (X \le x, Y \le y ) \end{align}\]

上面的 $F(x,y)$ 称作随机变量 (X,Y) 的分布函数，也叫作联合分布函数。

离散型随机变量联合分布

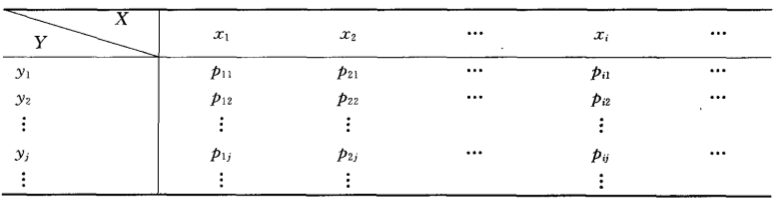
如果上面的 $X$ 和 $Y$ 都是离散随机变量，那么对于 $(X,Y)$ 的所有取值可记为

\[\begin{align} P(X=x_i, Y=y_i) = p_{ij},i,j=1,2,.... \end{align}\]

上面的所有 P 的取值为二维离散随机变量的分布律，也叫联合分布律。直观用表格表示如下所示

连续型随机变量联合分布

类似地，如果上面的 X 和 Y 都是连续随机变量，那么分布函数可定义为

\[\begin{align} F(x,y) = \int_{-\infty}^y\int_{-\infty}^xf(u,v)dudv \end{align}\]

其中 $f(x,y)$ 被称为概率密度函数，也叫联合概率密度函数。

其性质与一维随机变量的概率密度函数非常相似

\[\begin{align}f(x,y) \ge 0\]\begin{align}
\end{align}\[\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(x,y)dxdy = F(\infty,\infty)\end{align}\]

3. 设 $G$ 是 $xOy$ 平面上的区域，点 $(X,Y)$ 落在 G 内的概率为

\[\begin{align} P((X,Y)\in G) = \int\int f(x,y)dxdy \end{align}\]

4. 若 $f(x,y)$ 在点 $(x, y)$ 连续，则

\[\begin{align} \frac{\partial^2F(X,Y)}{\partial x \partial y} = f(x, y) \end{align}\]

边缘分布函数

二维随机变量 $(X,Y)$ 作为一个整体的时候，其分布函数为联合分布函数，但是 $X$ 和 $Y$ 是随机变量，各自也有分布函数，将其分别记为 $F_X(x),F_Y(y)$，称为随机变量 $(X,Y)$ 关于 $X$ 和关于 $Y$ 的边缘分布函数。

边缘分布函数可通过联合分布函数确定，关系如下

\[\begin{align} F_X(x) = P(X \le x) = P(X \le x,Y \lt \infty) = F(x, \infty) \end{align}\]

即

\[\begin{align} F_X(x) = F(x,\infty) \end{align}\]

也就是说在联合分布函数 $F(x,y)$ 中令 $y \rightarrow \infty$ 即可得到边缘分布 $F_X(x)$, 同理 \[F_Y(y) = F(\infty, y)\]

下面分别以离散型随机变量和连续性随机基量为例说明

离散型随机变量边缘分布

假如 $X$ 和 $Y$ 是离散型随机变量，那么随机变量 $(X,Y)$ 关于 $X$ 和关于 $Y$ 的边缘分布定义下

\[\begin{align} p_{i.} = \sum_{j=1}^{\infty} p_{ij} = P(X = x_i), i=1,2,3.....n \end{align}\]

\[\begin{align} p_{.j} = \sum_{i=1}^{\infty} p_{ij} = P(Y = y_j), j=1,2,3.....n \end{align}\]

上面的式子分别称为随机变量 $(X,Y)$ 关于 $X$ 和关于 $Y$ 的边缘分布率。

连续型随机变量边缘分布

假如 $X$ 和 $Y$ 分别是连续性随机变量，那么随机变量 $(X,Y)$ 关于 $X$ 的边缘分布函数定义为

\[\begin{align} F_X(x) = F(x,\infty) = \int_{-\infty}^{x}(\int_{-\infty}^{\infty}f(x,y)dy)dx \end{align}\]

而

\[\begin{align} f_X(x) = \int_{-\infty}^{\infty}f(x,y)dy \end{align}\]

则被称为随机变量 $(X,Y)$ 关于 $Y$ 的 边缘概率密度函数

条件分布

由条件概率可以比较容易推导出条件分布的含义，其定义如下：

离散型随机变量的条件分布

对于离散型随机变量，条件分布的定义如下：

设 $(X,Y)$ 是二维离散型随机变量，对于固定的 $j$，若 $P(Y=y_j) \gt 0$, 则称 \[\begin{align} P(X = x_i|Y= y_j) = \frac{P(X = x_i, Y=y_j)}{P(Y=y_j)} = \frac{p_{ij}}{p_{.j}}, i = 1,2,3 \end{align}\] 为在 $Y=y_j$ 条件下随机变量 X 的条件分布律。同理，交换 $X$ 和 $Y$ 的位置得到的是在 $X=x_i$ 条件下随机变量 $Y$ 的条件分布律。

连续型随机变量的条件分布

对于连续型的随机变量，条件分布的定义如下：

设二维随机变量 $(X,Y)$ 的概率密度函数为 $f(x,y),(X,Y)$ 关于 $Y$ 的边缘概率密度为 $f_Y(y)$ . 若对于固定的 $y，f_Y(y) >0$ ，则称 $\frac{f(x,y)}{f_Y(y)}$ 为在 $Y=y$ 的条件下 $X$ 的条件概率密度。记为 \[\begin{align} f_{X|Y}(x|y) = \frac{f(x,y)}{f_Y(y)} \end{align}\]

有了条件概率密度 (就是条件概率密度函数)，我们也可以定义出条件分布函数如下

\[\begin{align} \int_{-\infty}^x f_{X|Y}(x|y)dx = \int_{-\infty}^x \frac{f(x,y)}{f_Y(y)}dx \end{align}\]

上面的函数为在 $Y=y$ 的条件下 $X$ 的条件分布函数，记为

$F_{X|Y}(x|y) = P(X \le x| Y=y)$

相互独立的随机变量

两个随机变量 $X,Y$ 相互独立的充要条件如下：

$F(x,y) = F_X(x)F_Y(y)$

上面的 $F(x,y),F_X(x),F_Y(y)$ 分别是二维随机变量的联合分布函数及关于 $X$ 和 $Y$ 的边缘分布函数。

除了通过分布函数，对于具体的连续型随机变量或离散型随机变量，还可通过概率密度函数和分布律来定义相互独立的条件。

对于连续型随机变量，上面的式子等价于

$f(x,y) = f_X(x)f_Y(y)$

式子中的 $f(x,y),f_X(x),f_Y(y)$ 分别为随机变量 $(X,Y)$ 的条件概率密度函数和边缘概率密度函数。

对于离散型随机变量则有：

$P(X = x_i, Y = y_j) = P(X=x_i)P(Y=y_j)$

二维随机变量的函数的分布

在讨论一维随机变量的分布函数的时候，也讨论了一维随机变量的函数的分布函数，同样对于二维随机变量，我们也可以讨论其函数的分布函数。下面主要讨论 $Z=X+Y$，$Z=XY$，$Z=Y/X$，$M=max(X,Y)$，$N=min(X,Y)$ 这几个函数的分布函数（$X，Y$ 为相互独立的随机变量），这里主要给出具体的公式，证明省略。

$Z = X + Y$ 的分布

设 $(X,Y)$ 是二维连续型随机变量，其概率密度函数为 $f(x,y)$， $Z = X+Y$ 仍然为连续性随机变量，其概率密度函数为

\[\begin{align} f_{X+Y}(z) = \int_{-\infty}^{\infty} f(z-y,y)dy \end{align}\] 或 \[\begin{align} f_{X+Y}(z) = \int_{-\infty}^{\infty} f(x,z-x)dx \end{align}\]

当 $X,Y$ 相互独立时，其边缘概率密度函数具有以下性质

$f(x,y) = f_X(x)f_Y(y)$

因此上面的式子也可以化成下面的形式

\[\begin{align} f_{X+Y}(z) = \int_{-\infty}^{\infty} f_X(z-y)f_Y(y)dy \end{align}\]

\[\begin{align} f_{X+Y}(z) = \int_{-\infty}^{\infty} f_X(x)f_Y(z-x)dx \end{align}\]

$Z=XY$ 和 $Z=Y/X$ 的分布

设 $(X,Y)$ 是二维连续型随机变量，其概率密度函数为 $f(x,y)$， $Z = \frac{Y}{X},Z = XY$ 仍然为连续性随机变量，其概率密度函数为

\[\begin{align} f_{Y/X}(z) = \int_{-\infty}^{\infty} |x|f(x,xz)dx \end{align}\]

\[\begin{align} f_{XY}(z) = \int_{-\infty}^{\infty} \frac{1}{|x|}f(x,z/x)dx \end{align}\]

当 $X,Y$ 相互独立时，同样有下面的性质

\[\begin{align} f_{Y/X}(z) = \int_{-\infty}^{\infty} |x|f_X(x)f_Y(xz)dx \end{align}\]

\[\begin{align} f_{XY}(z) = \int_{-\infty}^{\infty} \frac{1}{|x|}f_X(x)f_Y(z/x)dx \end{align}\]

$M = max(X,Y)$ 和 $N = min(X,Y)$ 的分布

讨论 $max(X,Y)$ 和 $min(X,Y)$ 的分布的时候，一般假设 $X, Y$ 相互独立，因为这样才有下面的性质。

对于 $M = max(X,Y)$ 的分布有

$F_{max}(z) = P(M \le z) = P(X \le z, Y \le z) = P(X \le z)P(Y \le z)$

由于 $X$ 和 $Y$ 相互独立，因此有

$F_{max}(z) = F_X(z)F_Y(z)$

同样对 $N = min(X,Y)$ 有

$F_{min}(z) = P(N \le z) = 1 - P(N \gt z) = 1 - P(X > z)P(Y>z)$

即

$F_{min}(z) = 1 - (1 - F_X(z))(1 - F_Y(z))$

推广到 $n$ 个相互独立的随机变量有下面的性质

$M = max \lbrace X_1,X_2...,X_n \rbrace$ 及 $N = min\lbrace X_1,X_2...,X_n \rbrace$ 的分布函数分别为

\[\begin{align} F_{max}(z) = F_{X_1}(z)F_{X_2}(z)...F_{X_n}(z) \end{align}\]

\[\begin{align} F_{min}(z) = 1 - (1 - F_{X_1}(z))(1 - F_{X_2}(z))...(1 - F_{X_n}(z)) \end{align}\]

而当 $ X_1,X_2...,X_n $ 独立同分布的时候，上式变为如下所示

\[\begin{align} F_{max}(z) = [F(z)]^n \end{align}\]

\[\begin{align} F_{min}(z) = 1 - (1 - F(z))^n \end{align}\]