《Reducing the Dimensionality of Data with Neural Networks》阅读笔记
Reducing the Dimensionality of Data with Neural Networks是对深度学习有重要影响的一篇论文，可以说是拉开了深度学习的帷幕，该论文出自 Hinton 大神之手。本文是读了论文后结合其他一些参考资料整理成的读书笔记。
简介
该论文主要讲述了通过神经网络对数据进行降维，并通过多项实验结果证明通过神经网络进行降维的效果要优于传统的降维方法 PCA(Principal component analysis, 主成成分分析)。但是要达到这种效果，需要有一个前提，那就是神经网络中的参数在初始化的时候不能随机初始化，而是要有一个预训练的过程，论文中通过 RBM(Restricted Boltzmann machine，受限玻尔兹曼机)来实现这个预训练的过程，利用 RBM 对神经网络中的参数进行逐层预训练，然后将训练出来的参数作为神经网络的初始化参数。
数据的降维
在机器学习中，原始数据往往会存在着各种各样的问题，样本的特征数目过多是其中之一，当样本的特征过多的时候往往会存在冗余的信息和噪声；而当特征数目原大于样本数目的时候容易导致过拟合，使得模型的泛化能力弱；除此之外，特征数目过多的样本也需要更长的训练时间，训练的成本较高。
基于上述的原因，在训练模型之前往往需要对数据进行一个降维的操作，常见的降维方法有 PCA 等。降维直观的反映就是样本特征数目的减少，同时原始的信息（包括有用的信息和噪声）也会有损失；从另外一个角度来看降维就是提取原始数据的主要特征，而神经网络的结构特点恰恰为其进行特征提取提供了可能性，下面就讲述如何通过神经网络进行特征的提取，也就是论文的主要工作。
自编码器与逐层预训练
自编码器(autoencoder)是论文提出的一种特殊的神经网络，由
Encoder 和 Decoder 两部分构成，其中
Encoder 的作用是降维，而 Decoder
的作用是从降维的后的特征中恢复出原始特征。其结构如下所示：
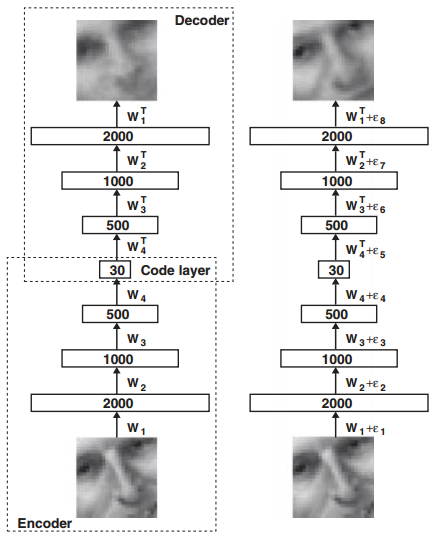
上图主要展示了通过自编码器对图像进行特征压缩并复原的过程。其中左边部分是初始训练时候的状态，Encoder
将原图像2000维的特征压缩到了30维， 而 Decoder
将压缩后得到的30维的图像恢复成原来的2000维，由于还没对网络进行训练，所以此时的图像会比较模糊。右边部分则是通过经典的
BP(Backpropagation, 反向传播)
算法对网络进行训练后的恢复效果，得到的效果与原图像已经非常接近了。
从上面的描述看来，自编码器的训练方法与传统的神经网络的训练没有差别。但是论文中指出了网络的初始化参数要足够好，才能利用这种训练方法得到比较好的效果。
网络的初始化参数就是上图中的 \(W_1,W_2,W_3,W_4\), 我们知道，神经网络的主要是通过前向传播和反向传播这两个过程来训练网络中层与层之间的参数，通过这些网络间的参数来拟合数据的内在特性。但是在开始训练前，必须要给网络中的参数赋一个初始值，由于对数据没有任何的先验知识，这种初始化赋值往往是随机的，在多层网络中随机初始化参数存在着以下问题：当随机初始化的值过大时容易陷入局部最优，当随机初始化的值过小时训练会比较困难（在反向传播的时候梯度很快趋于0，错误信息传不到前面的层）。
而论文中所说的“网络的初始化参数足够好”其实是要通过逐层训练的方法先训练出一批参数值作为初始值赋给 \(W_1,W_2,W_3,W_4\)，然后再进行后面的前向传播和反向传播来训练整个网络。
下面主要讲述如何训练出网络的初始化参数，而这也是本文的最重要的工作。
逐层预训练过程
在逐层预训练中采用的模型是 RBM, RBM 的结构图如下所示
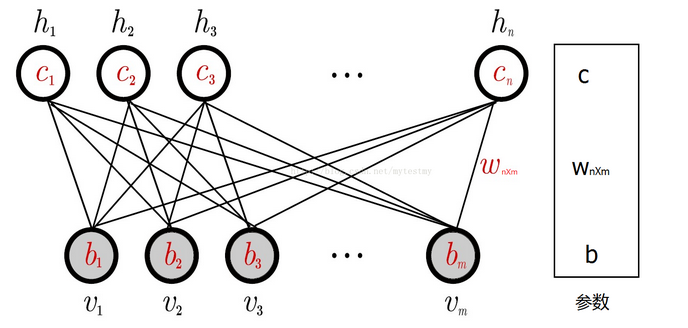
从上面的的结构图可知， RBM 是一个二层全连接的双向网络，二层指的是隐藏层(h节点)和可视层(v节点)，其中各层节点的大小关系没有要求（也就是 m可以大于n也可以小于n），双向指数据既可从可视层传播到隐藏层，也可从隐藏层传输到可视层。
RBM包含的参数有
- 权重矩阵 \(W_{nm}\)
- 隐藏层偏置量 \(c = (c_1, c_2, c_3, ... c_n)\)
- 可视层偏置量 \(b = (b_1, b_2, b_3, ... b_m)\)
其中偏置量的取值为0或1。
由于传播方向是双向的，这里先不加证明给出两个方向的传播的公式，具体的证明看下一节的原理与推导。
从可视层传到隐藏层\[P(h_i=1|v) = \sigma(\sum_{j=1}^mw_{ij}v_j+c_i)\tag{3-1}\] 从隐藏层传到可视层\[P(v_j=1|h) = \sigma(\sum_{i=1}^nw_{ij}h_i+b_j)\tag{3-2}\] 其中 \[ \sigma(x) = 1/(1+e^{-x})\tag{3-3}\]
由上面的传播公式可知，两个传播过程计算出来的都是一个概率值，就是传播的目标点取1的概率，实际中赋值时按照均匀分布产生一个0到1之间的随机浮点数，如果它小于\(P(v_j=1|h)，v_j\) 的取值就是1，否则就是 0。
有了上面关于 RBM 的基础知识，下面就是逐层预训练的具体过程
- 正向过程：样本 \(v\) 通过公式 (3-1) 从可视层输入得到 \(h\)
- 反向过程：隐藏层 \(h\) 通过公式 (3-2) 回传到可视层得到 \(v'\), 利用 \(v'\) 再进行一次正向传播得到隐藏层的 \(h'\)
- 权重更新过程：更新公式为(其中 \(\alpha\) 为学习率) \[W(t+1) = W(t) + \alpha(vh^T-v'h'^T)\tag{3-4}\]
- 迭代上面过程直至权重 \(W\) 收敛
上面的公式中的 \(v,h,v',h'\) 均为向量，且公式 (3-4) 在原文表述为 \(\Delta W_{ij} = \varepsilon ( (v_jh_j)_{data} - (v_jh_j)_{recon})\)，但是含义是一致的，就是利用被压缩后再恢复的数据与原始数据的误差来调整二层网络间的参数，使得恢复出来的数据尽可能与原始数据接近，也就是要让被压缩后的数据尽可能的保留着原始数据的特征。
上面的训练过程中只是训练了相邻两层网络间的参数，而神经网络一般是有多层的，所以需要利用这种方法逐层进行训练，这也是逐层预训练说法的来由。所以上面通过自编码器对图像进行特征压缩并复原的完整过程如下图所示：
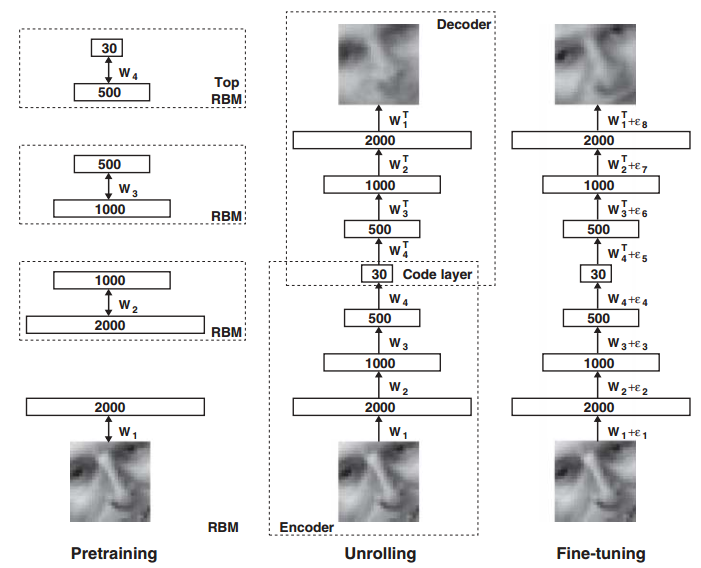
首先利用 RBM 逐层训练出网络的初始化参数，后面就是传统神经网络的训练过程了，通过前向传播和反向传播来调整网络间的参数，从而达到收敛。
原理与推导
上面主要讲述了参数逐层预训练的具体过程，下面主要讲述这种方法的思想以及推导对上面不加证明给出的传播过程的公式。
在自编码器预训练的过程中， RBM 的主要作用是在隐藏层尽可能保留从可视层输入的数据的主要特征（因为特征维度的压缩会导致数据的损失），而度量其保留程度的指标就是利用压缩了的特征恢复出来的图像与原图像的概率分布的差别，差别越小，保留的特征就越好。利用这个差别，可以调整 RBM 中的参数，从而使得误差逐步减小。
因此，上面的正向过程( \(v \rightarrow h\) )是一个特征压缩过程，影响了真实数据的特征，而反向过程( \(h \rightarrow v', v'\ \rightarrow h'\) )就是利用压缩后的特征(\(h\))重现真实数据的特征（\(v'\)）,权重更新过程则是利用他们的误差来更新权重矩阵，误差在这里表示为 \((vh^T-v'h'^T)\)。
上面的正向过程和反向过程中的两个关键公式 (3-1) 和 (3-2) 我们是不加证明的使用的，下面对其进行简单推导，推导的思路是从 RBM 的能量函数推导出概率模型，再从概率模型推导极大似然估计。
首先， RBM 诞生于统计力学，统计力学中为其定义的一个能量函数,针对下图的RBM
其能量函数表示如下：\[E(v,h) = -\sum_{i=1}^n\sum_{j=1}^m w_{ij}h_iv_j-\sum_{j=1}^mb_jv_j-\sum_{i=1}^nc_ih_i \tag{3-5}\]
定义出这个能量函数又有什么作用呢？根据参考资料，原因有以下几个 >第一、RBM网络是一种无监督学习的方法，无监督学习的目的是最大可能的拟合输入数据，所以学习RBM网络的目的是让RBM网络最大可能地拟合输入数据。
第二、对于一组输入数据来说，现在还不知道它符合那个分布，那是非常难学的。例如，知道它符合高斯分布，那就可以写出似然函数，然后求解，就能求出这个是一个什么样个高斯分布；但是要是不知道它符合一个什么分布，那可是连似然函数都没法写的，问题都没有，根本就无从下手。
第三，统计力学的结论表明，任何概率分布都可以转变成基于能量的模型，而且很多的分布都可以利用能量模型的特有的性质和学习过程，有些甚至从能量模型中找到了通用的学习方法。换句话说，就是使用能量模型使得学习一个数据的分布变得容易可行了。
因此，基于上面的能量函数，可以定义出一个可视节点与隐藏节点间的联合概率 \[P(v,h) = \frac{e^{-E(v,h)}}{\sum_{v,h}e^{-E(v,h)}} \tag{3-6}\]
该公式也是根据统计热力学给出的，具体参看参考文献。有了联合概率，就可以求出其条件概率如下所示：
\[P(v) = \frac{\sum_he^{-E(v,h)}}{\sum_{v,h}e^{-E(v,h)}} \tag{3-7}\] \[P(h) = \frac{\sum_ve^{-E(v,h)}}{\sum_{v,h}e^{-E(v,h)}} \tag{3-8}\] \[P(v|h) = \frac{e^{-E(v,h)}}{\sum_ve^{-E(v,h)}} \tag{3-9}\] \[P(h|v) = \frac{e^{-E(v,h)}}{\sum_he^{-E(v,h)}} \tag{3-10}\]
上面的这些概率分布也叫Gibbs分布，这样就完成了从能量模型到概率模型的推导，下面是从概率模型推导出极大似然估计。
现在回到求解的目标: 让RBM网络的表示Gibbs分布最大可能的拟合输入数据的分布。那么这两个分布的KL散度如下所示,KL散度主要用于表示两个分布的一个相似度，其值越小，表示两个分布越相似： \[KL(q||p) = \sum_{x \epsilon \Omega} q(x) ln\frac{q(x)}{p(x)} =\sum_{x \epsilon \Omega} q(x)lnq(x)-\sum_{x \epsilon \Omega} q(x)lnp(x) \tag{3-11}\]
上式中的 \(q(x)\) 是输入样本的分布，样本确定的时候，该分布也确定了下来，而\(p(x)\)表示通过 RBM 后输出样本的分布，也就是公式 (3-8) 表示的隐藏层的分布。当输入样本确定的时候，要最小化公式 (3-9)的KL距离，实际上就是要最大化公式(3-9)中的 \(lnp(x)\),而 \(lnp(x)\) 与 RBM网络中的参数相关，实际上就是进行一个极大似然估计求出网络中的参数。具体的数学推导过程参见这里。通过求解便可以得到公式(3-1) 和 (3-2),也就完成了从概率模型到最大似然的推导。
实验效果对比
论文通过若干的实验证明了通过自编码器对图像进行压缩后再恢复的效果要优于PCA，需要注意的是图像的压缩实际上就是特征的压缩，也就是一个特征提取或者说降维的过程，下面是具体的实验结果。
### 实验一：曲线图像的压缩与恢复 下图是实验数据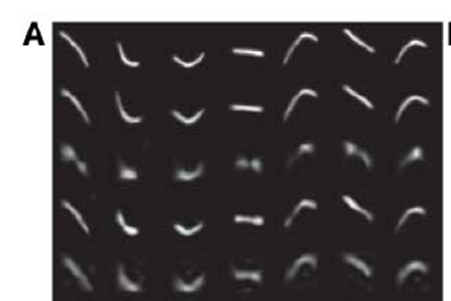 
上图中从上到下每一行对应于下表中从上到下的每一行
| 方法 | 特征数 | 均方误差 |
|---|---|---|
| 原图像 | 786 | |
| 自编码器 | 6 | 1.44 |
| PCA | 6 | 7.64 |
| Logistic PCA | 18 | 2.45 |
| PCA | 18 | 5.90 |
实验二：手写数字图片的压缩、恢复与分类
该实验采用 MNIST 数据集，下图是实验数据 
上图中从上到下每一行对应于下表中从上到下的每一行
| 方法 | 特征数 | 均方误差 |
|---|---|---|
| 原图像 | 786 | |
| 自编码器 | 30 | 3.00 |
| Logistic PCA | 30 | 8.01 |
| PCA | 30 | 13.87 |
上面是对图像进行压缩与恢复的实验，下面是提取每个手写数字两维的特征（原始维度为786维）进行分类的结果，图A是原始数据进行分类后的结果，图B是通过自编码器中的
Encoder
压缩到两维后再分类的结果。可以看到，通过自编码器得到的两维特征已经能够将各个数字较好分离开。
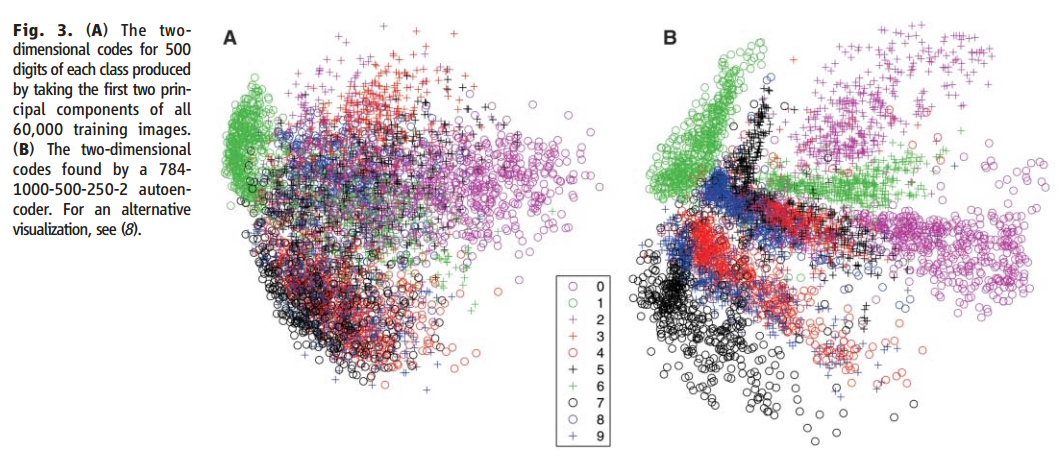
实验三：人脸图像的压缩与恢复
实验数据如下所示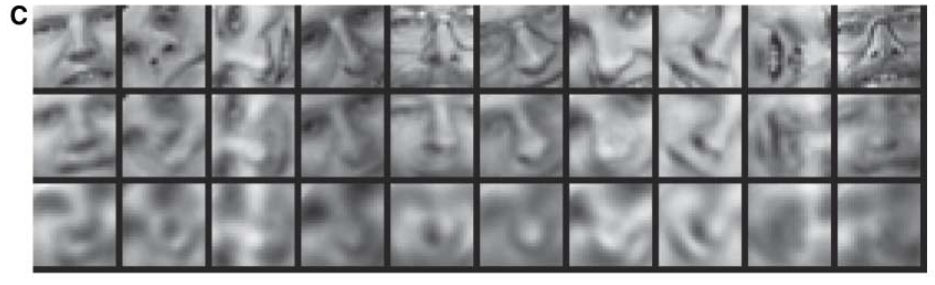 
上图中从上到下每一行对应于下表中从上到下的每一行
| 方法 | 特征数 | 均方误差 |
|---|---|---|
| 原图像 | 625 | |
| 自编码器 | 30 | 126 |
| PCA | 30 | 135 |
实验四：词向量的降维与分类
上面的实验均是针对图像的，但是实际上通过自编码器中的
Encoder
对原始数据进行提取特征后，可利用这些特征进行分类和回归。这个实验就是对词向量进行降维后并进行分类，主要比较自编码器和LSA(
Latent Semantic Analysis, 隐性语义分析)对词向量降维后分类的效果。
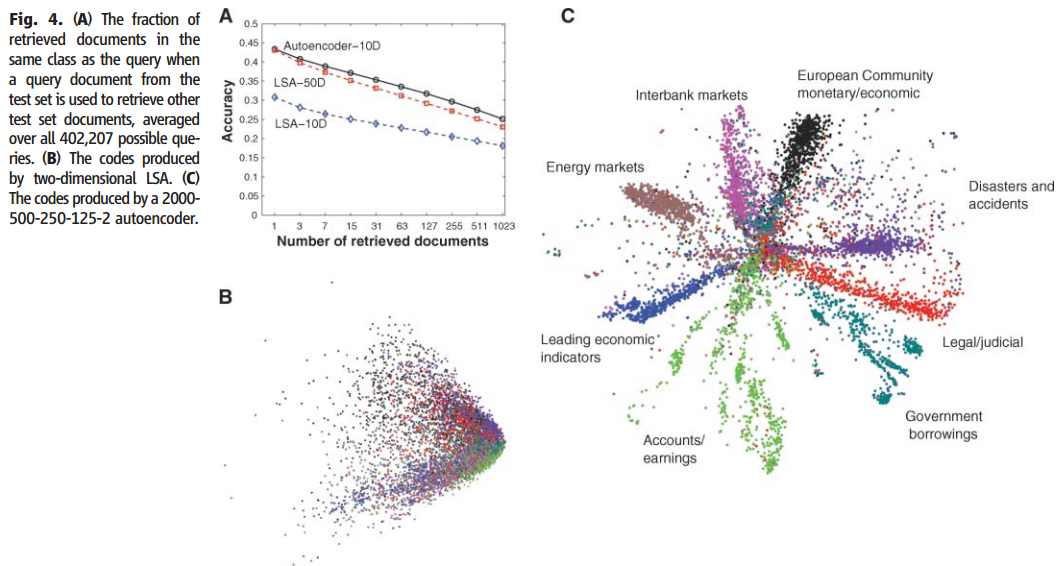
上图中 A 是文档相似性判断的准确率，通过LSA分类要提取文档向量的50维才能达到自编码器提取前10维进行分类的效果，图 B 是采用LSA对提取了2维的词向量(原始为2000维)进行分类的结果，可以看到完全无法分开，而图c是自编码器提取2维后的分类结果，可以看到分类结果要大大优于图B的效果。
总结
这篇论文由深度学习的开山鼻祖Geoffrey E. Hinton 2006 年发表在 science 上，论文虽然只有短短的四页，但是做了两个非常重要的工作
(1) 多层的神经网络具有优秀的特征学习能力，能够学习到数据更本质的特征 (2) 多层神经网络的初始化参数可通过逐层预训练获得
从上面的四个实验结果中可以看到自编码器提取的特征均要优于传统的PCA和LSA，也就是上面说的第(1)点；但是多层的神经网络很早就已经提出了，只是因为一直存在着初始化参数赋值的困难（过大陷入局部最优，过小梯度消失）而无法应用到实际中，本论文通过 RBM 逐层预训练得到多层神经网络的初始化参数，从而解决了这个问题，也就是上面说的第(2)点，也正是这个工作为多层神经网络或者说深度学习在实际中的应用拉开了帷幕。
参考文献： Reducing the Dimensionality of Data with Neural Networks 深度学习读书笔记之RBM（限制波尔兹曼机） 能量模型(EBM)、限制波尔兹曼机(RBM) 深度学习方法：受限玻尔兹曼机RBM（一）基本概念 深度学习方法：受限玻尔兹曼机RBM（二）网络模型