遗传算法简介

发表于 2017-04-10 标签数学

最近由于课程需要去调研了一下遗传算法，本文是调研结果的总结，主要介绍遗传算法的背景、基本流程、理论基础、变种及其应用。

连续优化与组合优化

连续优化

连续优化 (continuous optimization) 在某些教材中也被称为函数优化，其特点是变量的取值是连续的，或者说是变量的范围是实数域 (绝大多数情况)。对于一个可行域，其中包含着无数个可行解，这类问题一般利用目标函数可导的性质，通过如梯度，海塞矩阵等进行求解（如常见的梯度下降法，牛顿法等）。更详细的关于连续优化的方法可参考这篇文章

组合优化

相对于连续优化的另外一种优化是组合优化，组合优化的变量是离散的，也就是变量的空间只有有限多个的可行解。比如说经典的背包问题就是一个组合优化问题

既然只有有限多个解，那么最直接想到的求解方法就是通过穷举这些解 (exhaustive search) 找到最优解，然而分析可知，穷举所需要的时间复杂度一般是指数级别的，比如说对于背包问题，有 $n$ 个物品的时候，共有 $n^2$ 种可能性，时间复杂度是 $O(2^n)$。这样的问题已经是一个 NP-hard 问题了，这里先简单介绍一下 P 问题，NP 问题和 NP-hard 问题的区别。

一般来说，P 问题指的是能够在多项式时间复杂度内找到解的问题，而 NP 问题指的是无法在多项式时间复杂度内找到答案的问题，但是能够在多项式时间复杂度内验证一个解是否正确的问题（如大素数的判断问题）；而 NP-hard 问题则是指那种不仅无法在多项式时间复杂度内找到答案，甚至无法在多项式时间复杂度内验证一个解是否正确的问题（如背包问题，如果要找到最优，就必须对所有的可能进行比较，这样的时间复杂度就是指数级别了）。

实际上，大多数的组合优化问题都是 NP-hard 问题，虽然存在着某些特殊问题可以用多项式时间的方法来解决，如通过维特比算法求解 HMM 中最大概率的隐含状态转移路径。但是更多的情况下组合优化问题仍然是一个 NP-hard 问题。

于是为了解决这类得到最优解就需要耗时非常长的问题，人们退而求其次，去找一个接近最优解但是耗时在可接受范围内的解。进而诞生了一类方法: 元启发式方法 (Metaheuristic)。

元启发式方法 (Metaheuristic)

元启发式方法 (Metaheuristic) 是一类方法，维基上对的定义如下 >a metaheuristic is a higher-level procedure or heuristic designed to find, generate, or select a heuristic (partial search algorithm) that may provide a sufficiently good solution to an optimization problem

元启发式方法的定义中已经说得很清楚了，这一类方法不确定能够提供最优解，但是会提供一个足够好的解，当然这个足够好好到什么程度也是与具体算法相关的，需要通过数学证明。但是这类方法能够在可接受时间内返回这个解。

我们经常听到的一些算法都属于这种元启发式算法，包括：

遗传算法 (Genetic Algorithms，GA)
模拟退火 (Simulated Annealing，SA)
蚁群算法 (Ant Colony Optimization，ACO)
粒子群算法 (Particle Swarm Optimization，PSO) ......

这一类算法都是从自然现象中得到启发的，如遗传算法就是从进化论中得到启发的，认为 “物竞天择，适者生存”，一代代进化的基因是逐渐往好的方向发展的，对应到优化问题中就是逐渐收敛到比较好的解；模拟退火则是从金属加热后再冷却，金属中的分子最终有可能会到达一个内能比原来更低的位置，表示为一个更优解；蚁群算法和粒子群算法则是通过一个群体去搜索最优解，如对于非凸的优化，往往具有多个局部最优解，通过一个群体去搜索能够扩大搜索范围，从而以更大的概率收敛于全局最优解。

关于元启发式方法在组合优化中的更详细的应用可这篇文献： Metaheuristics in Combinatorial Optimization: Overview and Conceptual Comparison

遗传算法

从前面可知，遗传算法是元启发式方法的一种，维基上对其的定义如下:

Genetic algorithms are commonly used to generate high-quality solutions to optimization and search problems by relying on bio-inspired operators such as mutation, crossover and selection。

从维基的描述可知，遗传算法是收生物进化论的影响，因此遗传算法中的很多概念跟生物进化中的很多概念类似，而遗传算法主要的三个操作就是选择 (selection)，交叉 (crossover) 和编译 (mutataion).

下面先介绍遗传算法中的基本概念：

基本概念

个体（individual） : 一个候选解
种群（generation） : 一组候选解，代表某一代的所有个体
染色体（chromosomes） : 候选解的染色体表示，常见的用 01 字符串表示
适应度（fitness） : 个体的适应度，一般与优化问题中的目标函数值相关
选择（selection）: 根据个体适应性从一个 generation 中选出适应性好的进入下一代
交叉（crossover） : 类似于生物中两个个体进行杂交，两个 chromosomes 进行相应的交叉
变异（mutation）: chromosomes 的某一位进行突变，如从 0 变到 1 或从 1 变到 0

在执行遗传算法前，有两个东西必须先定义好

可行解的表示方法，也就是常说的编码方式，上面说到了常用的有 01 编码，除此之外，根据问题的不同，还存在其他的一些编码方式
适应度函数，也就是计算上面适应度的函数，这个函数一般 yong 就是用目标函数，如要最大化某个函数，则将这个函数作为目标函数即可，反之最小化的时候加个负号即可。

遗传算法是一个迭代算法，在进行初始化后按照 “选择，交叉，变异” 的顺序进行迭代，当满足设定的结束条件 (例如达到一定的代数)，便将得到的解作为问题的解。其流程如下所示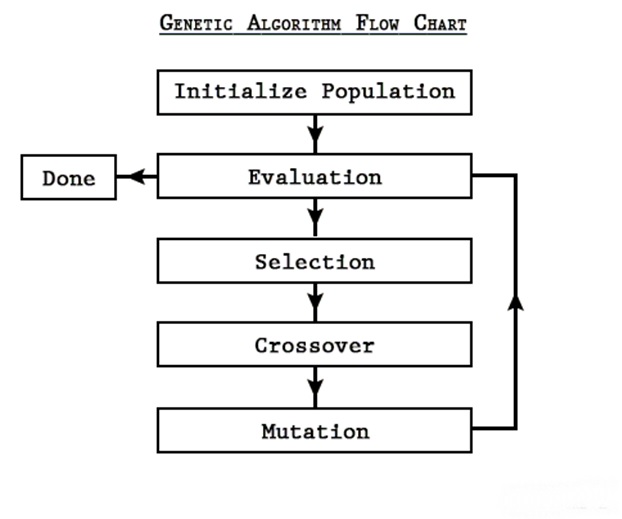

算法流程

初始化 (Initialization)

初始化主要是确定编码方式以及初始种群的数目，初始种群的数目由人为设定然后随机产生，设定的数目如果太小，可能会一开始就限制了搜索域较小，而如果设定的数目太大，计算量会比较大。

编码方式则根据问题的约束条件和希望得到的解的精度确定，后面会给出一个详细的例子说明这个问题。

选择 (Selection)

选择模拟了生物进化中的 “适者生存”，根据当代的个体的适应度按概率选出下一代，适应度越高，则被选择的概率也越大。

之所以不直接将适应度最大的若干个个体作为下一代，是因为这样可能会导致算法过早陷入局部最优解。在遗传算法里面这种现象称为 "早熟（premature）"。

假如当代的个体总数是 $M$，而个体 $a_i$ 的适应度是 $f_i$，则个体 $a_i$ 被选择到下一代的概率是 \[\begin{align} p_i = \frac{f_i}{\sum_{j=1}^{M} f_j} \end{align}\]

交叉 (crossover)

交叉跟生物上的杂交是一样的，只是生物中是双螺旋结构，而遗传算法中只有一条链。原始的遗传算法只会选择一个点进行交叉，如下如所示

而假如对遗传算法进行改进，也可以在多个点进行交叉的操作

交叉（crossover）的目的是从目前的所有解中组合出更优的解，但是尝试获得更优解的同时，也可能丢掉目前得到的最优解。而这也是传统的遗传算法无法收敛到全局最优的一个原因（详见后面的理论证明，对其进行了简单改进后可以收敛到全局最优）。

交叉是按照一定的概率进行的，这个概率也需要人为设定，假如设得过大边很容易将当前的最优解破坏掉，并且容易陷入早熟 (premature)，而设得过小时则很难从当前的可行解中组合出更优的解。

变异 (mutation)

变异（mutation）跟生物中的变异也一样，随机改变染色体中的某一位，如下所示就是一个变异的示例

变异也是按照一定的概率进行的，这个概率也需要人为设定，而且这个概率一般会设置得比较小，如果设得较大时，就变成了类似随机搜索（random search）的方法；但是如果设得太小的时候，就会造成生物中的基因漂变 (genetic drift) 的现象，从而导致收敛到一个局部最优。

变异的主要作用是为了防止算法收敛到一个局部最优解。假如将找到最优解比作在多座山峰中找到最高的那一座，那么交叉就类似同一座山峰下的多个基因合力爬上山顶，而变异就类似于从一座山峰调到另外一座山峰，目的就是为了防止当前的山峰是一个局部最优解而将算法其作为一个全局最优解。

终止 (termination)

算法的终止条件由人为设定，一般是限制迭代的最大次数，或能够使用的最大的计算资源，或者是两次的解小于某个设定的阈值，下面是从维基百科中摘录的终止条件

A solution is found that satisfies minimum criteria

Fixed number of generations reached
Allocated budget (computation time/money) reached
The highest ranking solution's fitness is reaching or has reached a plateau such that successive iterations no longer produce better results
Manual inspection
Combinations of the above

例子

下面给出两个例子：分别是遗传算法解决背包问题和一个连续优化问题。

遗传算法解决背包问题

背包问题是一个很经典的组合优化问题，通过遗传算法可以求解，但是目前求解这类问题的最优方法是动态规划，是一个伪多项式时间复杂度问题。这里采用背包问题为例子是因为这个例子的编码方式有较好的解释。

假设现在背包的容量为 $W$, 共有 15 个物品，每个物品的大小为 $w_i$, 价值为 $v_i$, 则可以得到下面的最优化问题

\[\begin{align}max \sum_{i=1}^{15} x_iv_i\\ s.t. \sum_{i}w_ix_i \le W\\ x_i \in \lbrace 0,1 \rbrace\end{align}\]

$x_i \in \lbrace 0,1 \rbrace$ 表示是否将第 $i$ 件物品放到背包中。

则通过遗传算法解决这个问题的流程如下

初始化 由于有 15 个物品，而每个物品只有两个状态，因此用一个长度为 15 的 01 字符串表示一个解，0 表示不拿该物品，1 表示那该物品。随机产生 10 个候选解如下所示，这里要注意每个候选解必须要满足约束条件

由于没有给出每个物品具体的价值，这里用 $V_i$ 表示第 $i$ 个候选解通过公式 $\sum_{j=1}^{15}x_jv_j$ 求得的总价值。

选择

由于每个个体被选择到下一代的概率与其适应度成正比，因此第 $i$ 个候选解被选择到下一代的概率为 \[p_i = \frac{V_i}{\sum_{j=1}^{15}V_j}\]

如下为模拟的过程，注意一个个体可能会被选择多次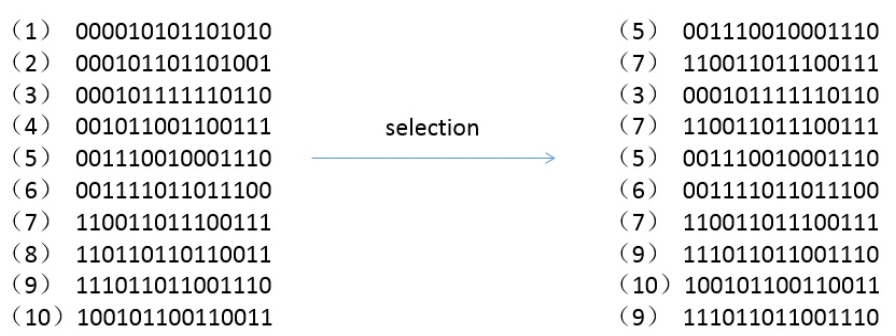

交叉

对选择出来的个体重新进行编号，然后进行交叉的操作，按照设定的交叉概率选择个体进行交叉的操作，交叉的位置也是随机产生的，如下所示是设定交叉概率为 0.5 后的交叉结果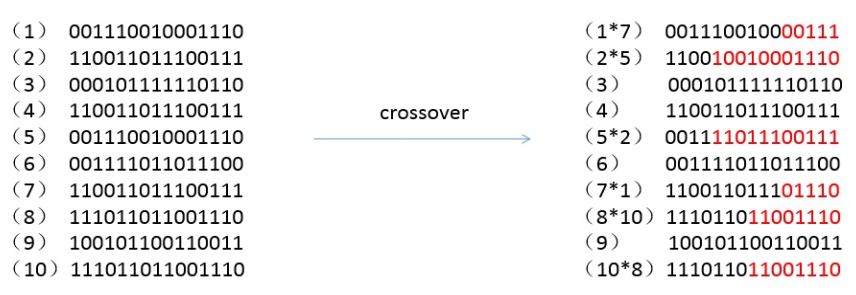

变异

变异也是按照变异概率选择个体来进行的，被选中的个体变异的位数可以是一位也可以是多位，如下图所示是设定变异概率为 0.2 的编译过程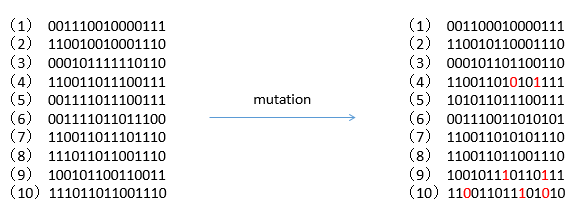

终止

设定一个终止条件，如最大的迭代次数，当满足这个条件时边终止算法，将当前得到的最优解作为问题的最优解；没满足时便按照 "选择 -> 交叉 -> 编译" 进行迭代。

利用遗传算法求解背包问题更详细的信息可参考这篇文献：A genetic algorithm for the multidimensional knapsack problem

遗传算法解决连续优化问题

该例子来源于知乎，优化的问题如下所示

\[\begin{align} \max f(x) = x + 10sin(5x) + 7cos(4x)， x \in [0,9] \end{align}\]

这个函数的图像如下所示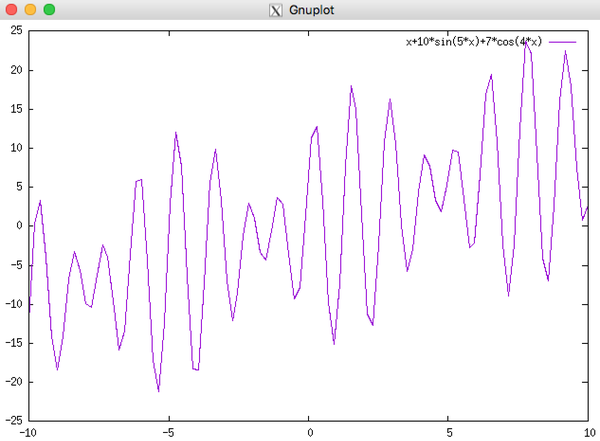

显然这已经不是一个凸函数了，通过遗传算法解决这个问题的步骤跟背包问题的一样，最主要也是最重要的区别在于编码方式的不同。

由于现在可行解是实数域了，仍旧采用 01 编码，则要解决的问题就是如何用 01 串表示一个实数。假设现在希望解精确到小数点的后四位，

假如设定求解的精度为小数点后 4 位，可以将 x 的解空间划分为 $(9-0)×10^4=90000$ 个等分。

由于 $2^{16}<90000<2^{17}$，则需要 17 位二进制数来表示这些解。换句话说，一个解的编码就是一个 17 位的二进制串。

一开始，这些二进制串是随机生成的。一个这样的二进制串代表一条染色体串，这里染色体串的长度为 17。对于任何一条这样的染色体 chromosome，如何将它复原 (解码) 到 [0,9] 这个区间中的数值呢？对于本问题，我们可以采用以下公式来解码：

x = 0 + decimal(chromosome)×(9-0)/(2^17-1)

decimal( ): 将二进制数转化为十进制数

更一般化的解码公式：

f(x), x∈[lower_bound, upper_bound] x = lower_bound + decimal(chromosome)×(upper_bound-lower_bound)/(2^chromosome_size-1)

lower_bound: 函数定义域的下限 upper_bound: 函数定义域的上限 chromosome_size: 染色体的长度通过上述公式，我们就可以成功地将二进制染色体串解码成 [0,9] 区间中的十进制实数解。

后面的选择，交叉，变异的过程与上面的背包问题一样，这里不在给出，在经过 100 次迭代后，最终选出的最优个体为 00011111011111011，其适应度，也就是目标函数的值为 24.8554，对应的 $x$ 为 7.8569, 从图像来看，已经是在最优解的位置了。

理论基础

上面介绍的内容仅仅是遗传算法的基本流程，但是经过这些仿生的操作能确保最终收敛吗？如果收敛的话能够收敛到全局最优还是局部最优？收敛到全局最优的概率是多少？

在遗传算法刚提出来的时候为不少问题找到了一个较好的解，对于很多问题都能找到一个比较好的解，但是缺乏数学理论基础的保证，往往会让人产生上面这些问题。

很多时候，实践的发展往往是超前于理论的，于是在遗传算法提出 5 年后，它的提出者便发表了模式定理 (Schema Theory) 来说明遗传算法中发生 “优胜劣汰” 的原因。而后又有人通过马氏链证明了算法的收敛性，结果是原始的遗传算法并不能收敛到全局最优，但是经过简单改进的遗传算法能够收敛到全局最优。

模式定理 (Schema Theory)

基本概念

问题引入：求解方程 $F(x) = x^2$ 在 [0,31] 上的最大值，使用固定长度二进制编码对种群中的个体进行编码，在计算适应度值时会发现一个规律，当个体编码的最左边为 1 时，适应度普遍较大，可以记为 1***1，同理 0**** 的个体适应度偏低。由此可以引入以下一些基本概念：

模式 (Schema)：编码的字符串中具有类似特征的子集。例如上述五位二进制字符串中，模式 *111* 可代表 4 个个体。个体和模式的一个区别就是，个体是由 {0，1} 组成的编码串，模式是由 {0，1，*} 组成，* 为通配符。

模式阶 (Schema Order)：表示模式中已有明确含义的字符个数，记为 o (s)，s 代表模式。例如 o (111)=3; 阶数越低，说明模式的概括性越强，所代表的编码串个体数也越多。其中阶数为零的模式概括性最强。

模式定义长度 (Schema Defining Length)：指第一个和最后一个具有含义的字符之间的距离，其可表示该模式在今后遗传操作中被破坏的可能性，越短则越小，长度为 0 最难被破坏。

下面就是模式定理的具体定义： > 适应度高于群体平均适应度的，长度较短，低阶的模式在遗传算法的迭代过程中将按指数规律增长。

下面将推导经过选择，交叉和变异后如何得到上面的模式定理

选择

假设当前是第 $t$ 代，这一代中模式 $s$ 的个体数记为 $m(s,t)$，整个种群的数目为 $M$，个体 $a_i$ 的适应度为 $f_i$

则个体 $a_i$ 被选择的概率为 \[p_i = \frac{f_i}{\sum_{j=1}^{M} f_j}\]

因此经过选择后，模式 $s$ 在下一代的数目为

\[\begin{align} m(s, t+1) = M\frac{m(s,t) \overline {f(s)}}{\sum_{j=1}^{M} f_j} = m(s,t) \frac{\overline {f(s)}}{\overline {f}} \end{align}\]

其中 $\overline {f(s)}$ 表示模式 $s$ 中个体的平均适应度，$\overline f$ 表示整个种群的平均适应度，也就是 \[\overline f = \frac{\sum_{j=1}^{M} f_j}{M}\]

可知只有当 $\overline {f(s)} > \overline f$, 模式 $s$ 中的个体才能增长，将上面的公式做简单的变化，则有

\[\begin{align} m(s, t+1) = m(s,t) \frac{\overline {f(s)}}{\overline {f}} = m(s,t) \frac{(1+c)\overline f }{\overline {f}} = m(s,t)(1+c) \end{align}\]

则从开始到第 $t+1$ 代，模式 $s$ 的个体的数目为: \[\begin{align} m(s, t+1) = m(s, t)(1+c)^t \end{align}\]

可以看到当模式平均适应度高于种群是适应度时，模式中的个体会呈指数形式增长。

交叉

记模式定义长度 (schema defining length) 为 $\delta(s)$，染色体的长度记为 $\lambda$

则模式被破坏，也就是在定义长度内进行交叉的概率为 $p_d = \frac{\delta(s)}{\lambda - 1}$

因此模式存活的概率为 $p_s = 1 - p_d = 1 - \frac{\delta(s)}{\lambda - 1}$

假设交叉概率为 $p_c$，则存活概率为 $p_s = 1 - p_c \frac{\delta(s)}{\lambda - 1}$

在经过选择，交叉后，模式 $s$ 在下一代数目为

\[\begin{align} m(s, t+1) = m(s,t) \frac{\overline {f(s)}}{\overline {f}}[1 - p_c \frac{\delta(s)}{\lambda - 1}] \end{align}\]

从这里可以看到，模式的定义长度 (schema defining length) 越小，则其存活的概率越大

变异

记模式的阶 (Schema Order) 为 $o(s)$，变异的概率为 $p_m$

则原来的基因存活，也就是那些确定的位置都不发生变异的概率为 \[p_s = (1-p_m)^{o(s)} \approx 1 - p_mo(s)\]

上式最后做了泰勒展开，因此经过选择，交叉和变异后，模式 $s$ 在下一代种群的数目为

\[\begin{align} m(s, t+1) = m(s,t) \frac{\overline {f(s)}}{\overline {f}}[1 - p_c \frac{\delta(s)}{\lambda - 1} - p_mo(s)] \end{align}\]

从上式也可以看到，模式的阶越低，模式约容易存活。

因此经过上面的分析，可以得到模式定理的定义

适应度高于群体平均适应度的，长度较短，低阶的模式在遗传算法的迭代过程中将按指数规律增长。

该定理阐明了遗传算法中发生 “优胜劣汰” 的原因。在遗传过程中能存活的模式都是定义长度短、阶次低、平均适应度高于群体平均适应度的优良模式。遗传算法正是利用这些优良模式逐步进化到最优解。

收敛性分析

虽然上面的模式定理说明了遗传算法有 “优胜劣汰” 的趋势，但是对于其收敛性并没有给出一个证明，这篇文献 Convergence Analysis of Canonical Genetic Algorithms 对遗传算法的收敛性进行了证明。

证明利用了有限状态的时齐马氏链的遍历性和平稳分布的性质，因为遗传算法可以被描述成一个有限状态的时齐马氏链，假如种群大小为 $M$, 染色体的长度为 $\lambda$, 采用 01 编码方式，将所有个体的染色体连起来作为一个状态，则种群的所有状态数目为 $2^{M\lambda}$。同时选择概率，变异概率和交叉概率可作为状态转移概率。

由于证明的定义和引理较多，因此这里不详细描述证明过程，只给出最后的结论。

证明给出的主要结论有两个： >1. 传统的遗传算法不能收敛到全局最优 >2. 在传统的遗传算法基础上每次选择的时候保留前面所有迭代里面的最优个体，最终能收敛到全局最优。

从证明最终给出的结论可知，传统的遗传算法并不能收敛到全局最优，证明过程指出的是收敛到全局最优的概率小于 1，原因就是选择、交叉和变异中都带有一定的随机性，这种随机性导致了最优解可能会被抛弃；而改进后的遗传算法每一代都会保留着前面所有代数的最优解，因此最终会以概率 1 收敛到全局最优。

改进方案 (Variants)

下面介绍的是对原始的遗传算法进行改进后得到的变种，改进主要有三大方向：编码方式 (Chromosome representation), 精英选择 (Elitism) 和参数自适应（Adaptive）。

编码方式

我们前面采用的均是 01 编码方式，但是实际上根据不同问题可以选择不同的编码方式，如格雷码（Gray Code）、浮点数编码都是可选的编码方式。

二进制编码的缺点是：对于一些连续函数的优化问题，由于其随机性使得其局部搜索能力较差，如对于一些高精度的问题（如上题），当解迫近于最优解后，由于其变异后表现型变化很大，不连续，所以会远离最优解，达不到稳定。

而格雷码能有效地防止这类现象，当一个染色体变异后，它原来的表现现和现在的表现型是连续的。主要优点有：

便于提高遗传算法的局部搜索能力
交叉、变异等遗传操作便于实现
符合最小字符集编码原则
便于利用模式定理对算法进行理论分析

这篇文献 An Improved Genetic Algorithm for Pipe Network Optimization 就适用了格雷码作为其编码方式。

而使用浮点数编码的原因往往是对连续函数优化时二进制编码精度不够。

精英选择

精英选择实际上就是在前面收敛性证明中改进遗传算法使得其以概率 1 收敛到全局最优的改进方案，在这篇文献中 Removing the Genetics from the Standard Genetic Algorithm 对其做了详细的描述。

参数自适应

前面我们说到了变异的概率和交叉的概率都是人为设定的固定值，但是实际上这个概率在不同的种群下应该会有其对应的最优值。因此这篇文献 Adaptive probabilities of crossover and mutation in genetic algorithms，将两个概率设定为下面的两个公式

\[\begin{align} P_c= \begin{cases} \frac{k_1(f_{max}-f')}{f_{max}-f_{avg}}&& {f' \geq f_{avg}}\\\ k_2 && {f' < f_{avg}} \end{cases}\]

\end{align}\[ P_m= \begin{cases} \frac{k_3(f_{max}-f')}{f_{max}-f_{avg}} && {f' \geq f_{avg}}\\\ k_4 && {f' < f_{avg}} \end{cases} \]\[\begin {align} 上面的公式表明，交叉率和变异率随着个体的适应度在种群平均适应度和最大适应度之间进行线性调整。上面的公式中 $f_{max}$ 表示种群的最大适应度，$f_{avg}$ 表示种群的平均适应度，$f'$ 表示参与交叉的两个个体中较大的适应度。由上面的公式可知，当适应度越接近最大适应度时．交叉率和变异率越小，好处是降低了最优解被破坏的概率，坏处是当前的最优适应度等于最大适应度时，交叉率和变异率为零。这使得 AGA 在演化初期并不理想。因为在进化初期的群体中，较优个体几乎处于一种不发生变化的状态，而此时的优良个体不一定是全局最优解，这容易使演化走向局部收敛的可能性增加。因此这篇文献 [自适应遗传算法交叉变异算子的改进][29] 对上面的公式进行了如下的改进 \end {align}\]\[ P_c= \begin{cases} p_{cmin}-\frac{（p_{cmax}-p_{cmin}）(f'-f_{avg})}{f_{max}-f_{avg}}&& {f' \geq f_{avg}}\\\ p_{cmax} && {f' < f_{avg}} \end{cases}\]

\[\begin{align} P_m= \begin{cases} p_{mmin}-\frac{（p_{mmax}-p_{mmin}）(f'-f_{avg})}{f_{max}-f_{avg}}&& {f' \geq f_{avg}}\\\ p_{mmax} && {f' < f_{avg}} \end{cases} \end{align}\]

$p_{cmin}$, $p_{cmax}$ 分别表示交叉率取值的下限和上限；而 $p_{mmin}$, $p_{mmax}$ 分别表示变异率取值的下限和上限，这样就避免了前面的概率出现 0 的情况。

参考文献

这些文献在上面已经在不同部分给出其相应的链接了，这里再次统一列出

Blum C, Roli A. Metaheuristics in combinatorial optimization: Overview and conceptual comparison[J]. ACM Computing Surveys (CSUR), 2003, 35(3): 268-308.

Chu P C, Beasley J E. A genetic algorithm for the multidimensional knapsack problem[J]. Journal of heuristics, 1998, 4(1): 63-86.

Goldberg, David .Genetic Algorithms in Search, Optimization and Machine Learning[M].MA: Addison-Wesley Professional, 1989:ISBN 978-0201157673

Rudolph G. Convergence analysis of canonical genetic algorithms[J]. IEEE transactions on neural networks, 1994, 5(1): 96-101

Srinivas M, Patnaik L M. Adaptive probabilities of crossover and mutation in genetic algorithms[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1994, 24(4): 656-667.

Dandy G C, Simpson A R, Murphy L J. An improved genetic algorithm for pipe network optimization[J]. Water resources research, 1996, 32(2): 449-458.

Baluja S, Caruana R. Removing the genetics from the standard genetic algorithm[C].Machine Learning: Proceedings of the Twelfth International Conference. 1995: 38-46.

Srinivas M, Patnaik L M. Adaptive probabilities of crossover and mutation in genetic algorithms[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1994, 24(4): 656-667.

邝航宇，金晶，苏勇。自适应遗传算法交叉变异算子的改进 [J]. 计算机工程与应用，2006, 42 (12): 93-96.