计算广告笔记 (2)-- 合约广告系统

发表于 2017-04-25 标签计算广告，机器学习

本系列文章是刘鹏老师的计算广告学中的一些记录。本文是第二章：合约广告系统，主要介绍了广告系统中一些常用的开源工具，合约广告系统的概念以及在线分配问题的建模与求解。

常用广告系统开源工具

广告系统中常用的工具有以下这些

总体可分为两类工具：离线与在线

离线

HBASE（列存储的 NOSQL 数据库，类似的有 BigTable，HyperTable，Cassandra）
Pig: 一种脚本语言
Elephant-bird：将二进制文件转为 pig 可处理的文本文件
Hive: 一种脚本语言
mahout: 分布式机器学习

在线

ZooKeeper/Chubby: 分布式环境下解决一致性问题
Avro/Thrift: 分布式环境下跨语言的通信问题
S4/Storm: 流式计算平台
Chuhwa/Scribe/Flume: data highway, 分布式日志收集工具，并送到其他平台

合约广告系统

合约广告有两个重要组成部分：广告位合约和展示量合约。

广告位合约：实际上是将线下的模式搬到了线上，指的是广告主与媒体约定在某一时间段内，在某些广告位上固定投放该广告主的广告，相应的结算方式是 CPT (Cost Per Time)（也就是按照展示时间结算），这种模式下售卖给广告主的是广告位。

展示量合约：展示量合约广告指的是约定某种受众条件下的展示量，然后按照事先约定好的单位展示量价格来结算，这种结算方式是 CPM (Cost Per Mille)（也就是每一千次展示的付费）。这种方式也叫担保式投放 (Guarantee Delivery, GD)，意思就是先广告主担保其提出的广告展示量会被满足。这种模式下售卖给广告主的是广告位 + 人群。

广告位合约

广告位合约对供给方和需求方的技术的要求都不高。

供给方即媒体往往会使用一种在合同确定以后自动的执行合同的广告管理工具：广告排期系统。广告排期系统能够帮助媒体自动执行多个合同的排期，可以将广告素材直接插入页面，且对于图片等静态资源，会放到 CDN 上进行加速。

需求方即广告主往往会通过代理商（agency）进行媒介采买（也就是广告位采买），代理商帮助广告主策划和执行排期，而对于广告的质和量，是根据代理公司人员对媒体广告位的历史经验以及对广告主业务的了解通过人工优化的方式来满足。这样的代理公司的代表有我们前面一讲提到的 4A 公司。

展示量合约

媒体从前面的广告位售卖变为按 CPM 的售卖，初衷是为了在受众定向的基础上提高单位流量的变现能力，可是面向的任然是原来的品牌广告主。广告主按广告位采买时，比较容易预估到自己能够拿到的流量，可是按照人群定向的方式采买，流量有诸多不确定的因素，因此，需求方希望在合约中加入对量的保证，才能放心购买。而假如约定的量未完成，则需要向广告商补偿。

因此，这种方式卖的不仅仅是广告位，而是人群。 后面半句我们很容易理解，而前面半句话的指的是在 CPM 这种结算方式下，任然没有摆脱广告位这一标的物，原因是无法将多个差别很大的广告位打包成统一售卖标的（这样的话每个广告主都会抢着要那些曝光率更高的广告位）；因此实际中的展示量合约往往是以一些曝光量很大的广告位为基础，再切分人群售卖，最典型的例子就是视频网站的铁片位置或者门户网站首页的广告位。

展示量合约这种模式的出现实际上已经反映了互联网广告计算驱动的本质：分析得到用户和上下文的属，并且由服务器端根据这些属性以及广告库情况动态决定广告候选。这一商业模式的出现，需要有一系列技术手段的支持，这些技术手段主要包括受众定向、流量预测、在线分配等。下面主要介绍流量预测和在线分配，受众定向会在下一讲中详细讲解。

流量预测

流量预测 (traffic forecasting) 简单来说就是预测某个标签的人群访问某个站点的量。流量预测其目的有多种，典型的有售前指导，在线流量分配，出价指导，前面两个是合约广告中的内容，而后面一个是竞价广告中的内容。

1）售前指导指的是在展示合约广告系统中，由于要约定曝光总数，事先尽可能准确地预测个人群标签的流量非常重要。因为如果流量低估，会出现资源售卖量不足的情形；而如果流量严重高估，则会出现一部分合约不能达成的状况。

2）在线流量分配指的是在展示量合约广告系统中，由于合约之间在人群的选择上会有很多的交集，因此一次的曝光往往会满足多个合约的要求，这时候就需要在多个合约之间进行分配，目的是达到整体满足所有合约的目的。这也是下面要详细探讨的在线流量分配的问题。

3）出价指导是竞价广告中的内容，在竞价广告中，没有了量的保证，广告主往往需要根据自己预计的出价先了解一下可能获得多少流量，以判断自己的出价是否合理。与前面在合约广告中的应用不同，这里还多了出价这一因素。

综上，广告里一般的流量预测问题，可以描述为对流量 $t(u,b)$ 这个函数的估计，其中 $u$ 是给定的人群标签或这些标签的组合，而 $b$ 是具体的出价。在展示量合约中，由于没有竞价，可以看成是 $b \rightarrow \infty$ 的特例。

在线分配

在合约广告系统中主要讨论在线分配（Online Allocation）问题，在线分配问题指的是在通过对每一次广告展示进行实时在线决策，从而达到在满足某些量的约束的前提下，优化广告产品整体收益的过程。

在线分配是广告中比较关键的算法框架之一，适用于许多量约束下的效果优化问题，而这实际上是广告业务非常本质的需求。

问题建模

在线匹配可看作是一个二部图匹配问题，二部指的是代表广告库存的供给节点（集合记为 $I$）和代表广告合约的需求节点（集合记为 $A$）。如下图所示，上边为集合 $A$, 下边为集合 $I$, 如果供给节点的受众标签能够满足某个需求节点的要求时，就在相应的两个节点之间建立一条连接边，所有边的连接记为集合 $E$。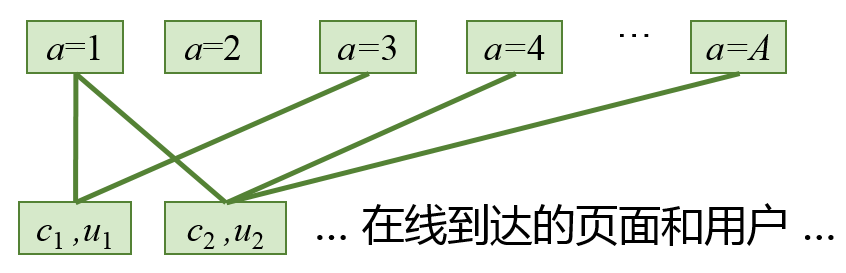

在线分配技术并不仅仅适用于展示量合约中的担保投放（GD）问题，还适用于 AdWords 问题，展示广告问题等。下面主要介绍 GD 问题和 AdWords 问题。

GD 问题

前面已经提到了 GD 的概念，在这里如果不考虑合约 $a$ 未完成的惩罚，收益一定是常数。那么 GD 的优化问题可以表示为

\[\begin{align} &\max \quad C\\\ &\begin{array}\\\ s.t. &\sum_{a \in \Gamma(i)} x_{ia} \le 1 &\forall i \in I\\\ &\sum_{i \in \Gamma(a)} s_i x_{ia} \ge d_a &\forall a \in A\\\ &x_{ia} \ge 0 &\forall (i,a) \in E \end{array} \end{align}\]

上面各式的符号含义如下

$C$ 是一个常数，指的是总收益 $I$、$A$、$E$ 上面已经提到，分别表示供给点集合，需求点集合，边的集合 $\Gamma(i)$ 表示与供给节点 $i$ 连接的所有需求节点的集合 $x_{i,a}$ 表示供给节点 $i$ 分配给需求节点 $a$ 的流量的比例 $\Gamma(a)$ 表示所有与需求节点 $a$ 连接的供给节点 $i$ 的集合 $s_i$ 表示供给节点 $i$ 的总流量 $d_a$ 表示需求节点 $a$ 的展示量需求

Adwords 问题

AdWorks 问题，也被称为有预算约束的出价问题，是竞价广告领域内的问题。简单来说，这个问题讨论的是在按照 CPC 方式结算的广告环境下，给定广告主的预算，整体化市场营收问题。需要注意的是，竞价广告中已经没有了量的约束，广告主给的约束是其预算费用。因此可以将这个问题表示为如下的优化问题

\[\begin{align} &\max_{(i,a) \in E} \quad q_{ia} s_i x_{ia}\\\ &\begin{array}\\\ s.t. &\sum_{a \in \Gamma(i)} x_{ia} \le 1 & \forall i \in I\\\ &\sum_{i \in \Gamma(a)} q_{ia}s_i x_{ia} \le d_a & \forall a \in A\\\ &x_{i,a} \ge 0 &\forall (i,a) \in E \end{array} \end{align}\]

上式大部分的符号跟 GD 问题相同，不同的地方主要是以下两个符号 $q_{ia}$ 表示需求节点 (广告主) $a$ 对供给节点（某个人群标签） $i$ 的出价 $d_a$ 表示则表示广告主 $a$ 的总预算

问题求解

上面的两个最优化问题均是线性规划问题，未知量是 $s_i$（供给节点 $i$ 的流量）和 $x_{ia}$（供给节点 $i$ 分配给需求节点 $a$ 的流量的比例）。但是对于 $s_i$ ，常常利用历史流量去估计它的值，因此上面的优化问题变成了仅仅需要求解 $x_{ia}$ 的问题。下面解决这个问题的几种思路

直接求解

对于这类线性规划问题，可以通过内点法或单纯形法直接进行求解，但是在大型的广告合约系统中，供给节点和需求节点的数目都很大，因此边 $|E|$ 的数目也会非常大（百万级以上), 这样会使得对应的分配问题变得过于复杂而无法直接有效求解。令 $n$ 为变量的个数，则内点的时间复杂度为 $n$ 的多项式级别，单纯形法的时间复杂度为 $O(n^2)$, 这样直接求解的解参数正比于 $|E|$ 的数量，规模有可能过于庞大，无法进行实时的在线分配。因此有必要探索更新效率更高的的在线分配方案。

对偶求解

通过拉格朗日对偶可将原问题装化为对偶问题，但是对偶问题的变量数目仍然正比于约束的数目（供给约束和需求约束），前者的变量的量级为十万甚至百万千万，但后者的量级在数千级别。

为了减少所需求解的变量，这篇文献 Optimal Online Assignment with Forecasts 提出了一个方法：只保留需求约束对应的对偶变量，然后通过数学变换恢复出供给约束对应的对偶变量和分配率。具体的算法过程可参考上面提到的文献。

上面的方法在求解对偶问题时代价仍然比较高，因此在文献 SHALE: an efficient algorithm for allocation of guaranteed display advertising 提出了 SHALE 算法，优化了求解对偶变量的步骤，采用了原始对偶方法迭代进行求解，求解出对偶变量后，通过数学变换恢复出供给约束对应的对偶变量和分配率跟上面的方法一致。

启发式分配方案 HWM

上面根据历史流量数据来求解的分配方案原理上可行，但是在实际的工程应用中仍然显得有些复杂，比如离线仍然要消耗大量的时间求解对偶解。因此，人们希望实现一种快速算法，保持前述方法的紧凑分配的特性，效果上也能够近似最优。前述方法中通过合同节点的对偶变量即可恢复最优解，受其讨论启发，可以发现，只要大体确定好每个合同在分配中的相对优先级以及分配时得到某次展示的概率，就可以构造出一种直觉上可行的在线分配方案。

文献 Ad serving using a compact allocation plan 提出的 HWM（High Water MArk）算法便是这样一种方案，虽然在数学上并不完全严谨，但是由于根据历史数据来指定的分配方案本身就具有相当程度的近似，因此其实际效果也不错，而工程上的便利性则是这个算法的一大优点。

HWM 分配算法有两个关键点： 1）根据历史流量确定每个广告合约资源的稀缺程度，通过可满足各合约的供给节点总流量的升序排列进而得到分配优先级 2）根据优先级确定每个广告合约的分配比例

具体过程可参考文献内容

合约广告系统主要模块

在前面提到的广告提供架构图中，合约广告系统主要表示为以下模块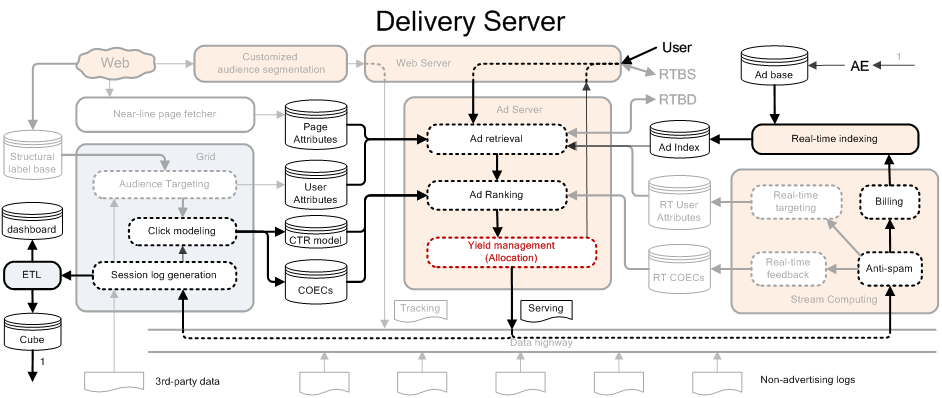

上面是竞价广告系统中截取出来的，但是截取出来的部分在概念上与合约广告系统相差不大；主要由以下几个部分构成

Ad retrieval：搜索页面内容相关的广告 Ad Ranking：计算 CTR，根据 CTR 排序 Yield management（Allocation）：广告分配的问题流量预测模块：跟 Allocation 打交道，在上图中没有画出来 Billing 和 Anti-spam：实时计算部分，用于计价和防作弊，任何广告系统都有

Hadoop 介绍

上面简单介绍了一些计算广告系统中常用的开源工具，下面主要介绍 Hadoop 这个使用最为广告的分布式系统。

Hadoop 源于 Lucene 项目一部分，2006 年成为子项目，后来成为 Apache 顶级项目

Hadoop 最为重要的两个部件： 1. HDFS：一个高可靠性，高效率的分布式文件系统 2. MapReduce: 一个海量数据处理的编程框架

HDFS

HDFS 的架构如下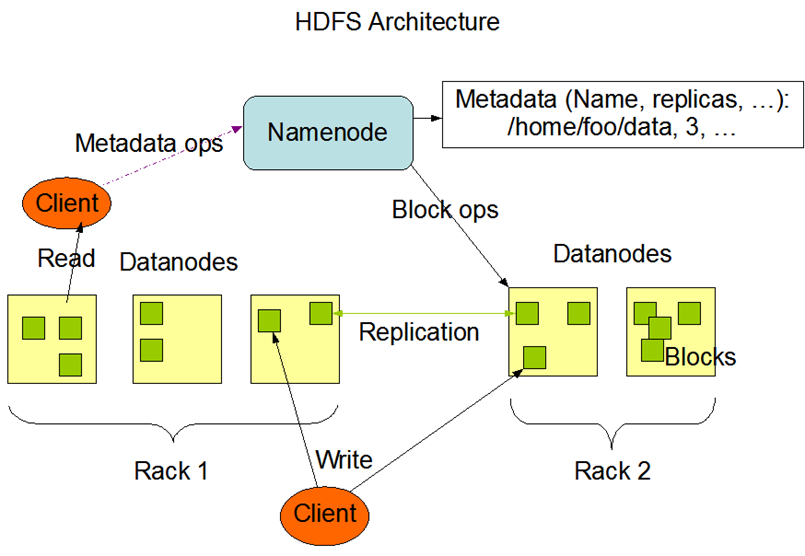： HDFS架构

HDFS 中主要有 Namenode 和 Datanodes 两种角色，其中 Namenode 存储的的是 metadata，其包含的信息是组成文件的各个 block 存储在哪个 Datanode 上，而 DataNodes 是真正存储文件数据的地方，并且为了达到高可用的效果，文件的一个 block 会以多个 replication 的方式存在多个 Datanode 上。

当 client 访问 HDFS 上的文件时，会先访问 NameNode，得到文件所在的 DataNode 的后再去对文件进行具体操作。

MapReduce

MapReduce 是一个分布式计算框架，整个过程包括一个 Map 过程和一个 Reduce 过程。相比于 MPI,Map 过程处理之间的独立性使得整个系统的可靠性大为提高；并且分布式操作和容错机制由系统实现，应用级编程非常简单。

MapReduce 的计算流程非常类似于简单的 Unix pipe

1 2	Pipe: cat input \| grep \| sort \| uniq -c > output M/R: Input \| map \| shuffle & sort \| reduce \| output

MapReduce 中进程间通信的时间只能是在 map 和 reduce 间的 shuffle & sort 过程，该过程主要是将经过 map 操作后 key 相同的那些记录聚合到一起，已进行后面的 reduce 操作。其过程如下图示：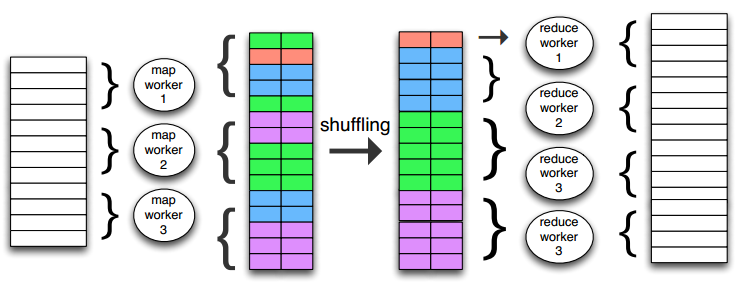

MapReduce 与分布式机器学习

在分布式机器学习中常用的统计模型有两种：指数族分布和指数族混合分布

指数族分布 (Exponential Family) 是条件概率服从某种形式的，常见的很多分布（如高斯分布，泊松分布，多项式分布等）通过变换都能够转化为这种形式，也就是常见的分布很多都是指数族分布。

这种分布的一个好处是通过最大似然 (Maximum likelihood, ML) 估计可以通过充分统计量 (sufficient statistics) 链接到数据，或者说得到数据的规律。这里的充分统计量 (sufficient statistics) 是指数族分布中的一个组成部分，一般来说就是模型的参数（如高斯分布的均值和方差）。

而当单个的指数族分布无法刻画数据的分布的时候，就要考虑多个指数族分布混合在一起的分布，也就是指数族混合分布；常见的指数族混合分布有 Mixture of Gaussians, Hidden Markov Models, Probabilistic Latent Semantic Analysis (PLSI) 等。

在指数族混合分布中， ML 估计一般通过 EM 算法迭代得到。每个迭代中，我们使用上一个迭代的统计量更新模型。

而一般的 ML 和 EM 算法能够通过 MapReduce 过程较好地刻画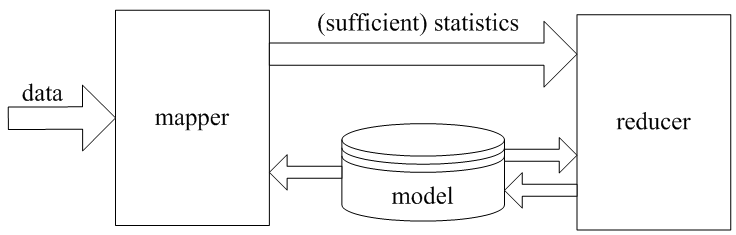

对于 ML 过程只需要一个 mapper 和一个 reducer 即可，上面从 reducer 经过 model 返回到 mapper 的过程代表 EM 的迭代过程。

这样刻画的好处使得在 mapper 中仅仅生成比较紧凑的统计量，其大小正比于模型参数量，与数据量无关；同时这样的流程可以抽象出来，而具体的模型算法只需要关注统计量计算和更新两个函数。

但是对于需要迭代的算法，MapReduce 需要与 HDFS 进行多次交互从而导致性能不佳，而这也是 Spark 等框架致力于解决的问题之一。

MapReduce 的多种实现方式

MapReduce 提供了多样的编程接口，除了上面介绍的直接通过 Java 写 MapReduce 程序外；通过 Streaming 可以利用标准输入输出模拟以上 pipeline；而通过 Pig 只需关注数据逻辑，无须考虑 M/R 实现

Hadoop 的 Streaming 模拟 Pipe 方式执行 Map/Reduce Job, 并利用标准输入 / 输出调度数据；开发者可以使用任何编程语言实现 map 和 reduce 过程，只需要从标准输入读入数据，并将处理结果打印到标准输出.

其限制是只支持文本格式数据，数据缺省配置为每行为一个 Record, Key 和 value 之间用 \t 分隔，如生成大量文本上的字典可通过下面的 linux 命令模拟 map 操作和 reduce 操作

1 2	map： awk '{for (i=1; i <=NF; i ++){print $i}}' reduce: uniq

Pig 通过类 SQL 操作在 Hadoop 上进行数据处理，如下是一段 pig 代码实例：

Users = load ‘users’ as (name, age); 
Fltrd = filter Users by 
    age >= 18 and age <= 25; 
Pages = load ‘pages’ as (user, url); 
Jnd = join Fltrd by name, Pages by user; 
Grpd = group Jnd by url; 
Smmd = foreach Grpd generate group, 
    COUNT(Jnd) as clicks; 
Srtd = order Smmd by clicks desc; 
Top5 = limit Srtd 5; 
store Top5 into ‘top5sites’;

Pig 解释器会进行整体规划以减少总的 map/reduce 次数，而如果需要通过 Java 来写 MapReduce 程序的话，会非常冗长，如下所示是实现相同功能的 MR 代码

pig 常用的一些语句如下所示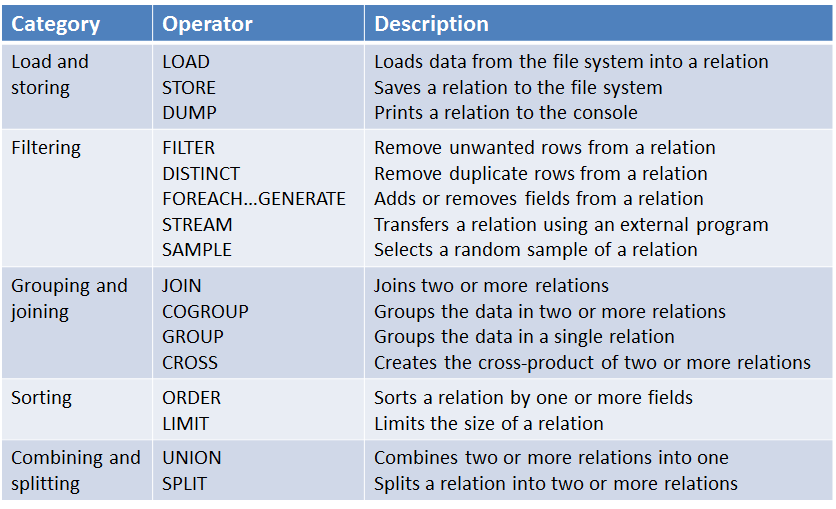

Hadoop 上还有一个工作流引擎：Oozie，用于连接多个 Map/reduce Job, 完成复杂的数据处理，处理各 Job 以及数据之间的依赖关系（可以依赖的条件：数据，时间，其他 Job 等); Oozie 使用 hPDL (一种 XML 流程语言) 来定义 DAG 工作流。这里需要注意的是工作流引擎在线上环境中非常重要，原因是当执行任务多了以后，任务间的关系依赖关系不能出错，否则会带来各种意想不到的后果。