计算广告笔记 (4)-- 竞价广告系统

发表于 2017-05-07 标签计算广告，机器学习

本文是刘鹏老师的计算广告学中的一些笔记。本文是第四章: 竞价广告系统。主要介绍竞价系统理论，广告网络的概念，以及点击率预测设计到的一些技术。

合约广告系统两个核心问题：在线分配和受众定向。

竞价广告系统是广告系统发展的里程碑。从搜索引擎的关键词的竞价延伸到展示广告，标签精细化的必然发展。

不保量，但是保质，量由 demand 端的 agency 保证。

竞价系统理论

竞价广告系统可以被描述成一个位置拍卖问题 (Position auctions)，该问题描述如下

该问题要解决的是将广告对象 $ a = , 2, … A $ 排放到位置 $ s = , 2, …, S $，这里的位置主要针对搜索广告而言
假设对象 $a$ 的出价 (bid) 为 $b_a$ , 而其对位置 $s$ 的计价为 $u_{as} = v_ax_s ,(x_1>x_2 >…>x_S)$， $v_a$ 视为点击价值，$x_s$ 视为点击率，该模型可近似描述广告系统竞价问题 (对显示广告，可以认为 S = 1，但是与搜索广告的不同点在于搜索广告可以一个都不出，而显示广告至少要出一个)
可以将问题描述成一个对称纳什均衡 (Symmetric Nash equilibrium) 其目标是 $(v_s – p_s) x_s >= (v_s – p_t) x_t $, 其中 $p_t = b_{s+1}$, 这里的 $p_s$ 表示根据广告的位置实际的收费情况，$b_{s+1}$ 在位置 $s+1$ 的广告的出价；寻找收入最大化且稳定的纳什均衡状态是竞价系统设计的关键

上面的问题建模比较复杂，需要较多的数学推导，这里主要关注上面问题建模求解以后得到的结论：就是定价机制该如何设置。这里讲的定价机制有两种：VCG (Vickrey–Clarke–Groves) 机制和广义第二高价 (Generalized second pricing) 机制。

从理论上来讲，VCG 机制是最优的，VCG 认为某对象的收费应等于给他人带来的价值损害，而且其有一个很好的性质：整体市场是 truth-telling 的，也就是每个广告主只需要根据自己真实想法出价，避免广告主间的博弈。

但是实际的定价机制是广义第二高价，就是每个位置收取的费用是其下一个位置的出价加 1（比下一个位置高即可）即 \[\begin{align} p_s = b_{s+1} + 1 \end{align}\] 这种做法看似会降低收益，但是实际上与 VCG 机制相比，会收取广告主更多的费用。关于原因，视频讲解时给了一个例子 > 假如说现在第一高价的广告是 5 块，第二高价的是 3 块。 > 假如采用第一高价的机制，那么出了第一高价的广告主就会设法调低自己的价格，比如说调到 3 块 1 毛，因为这时候仍然可以拿到第一位且支出更少，而如果再来一个人要第一的广告位，那么他可能就会调到 3 块 2； > 而采用第二高价的时候，出了第一高价的广告主不会设法调低自己的价格，因为收取的是第二高价的价格，而此时如果来了一个想要第一的广告位的广告主，那么他出的价格必须要在 5 元以上了

广义第二高价的整体市场不是 truth-telling 的，从上面的例子也可看到，商家之间会存在着博弈，但是由于其简单易行，为在线广告系统广泛采用，而 VCG 则用得较少

广告网络 (Ad Network)

维基百科对广告网络的定义如下： >Connects advertisers to web sites that want to host advertisements

在竞价广告系统中，其主要的特征有：

竞价系统 (Auction system)
淡化广告位概念：卖的是人群，而不是媒体，媒体已经变成了一个载体
最合适的计价方式为 CPC（Cost Per Click）: 非实时竞价方式，广告网络估计 CTR，广告主估计每个广告的价值
不足：不易支持定制化用户划分：广告主只能购买广告网络指定的关键词

广告网络的系统架构示意如下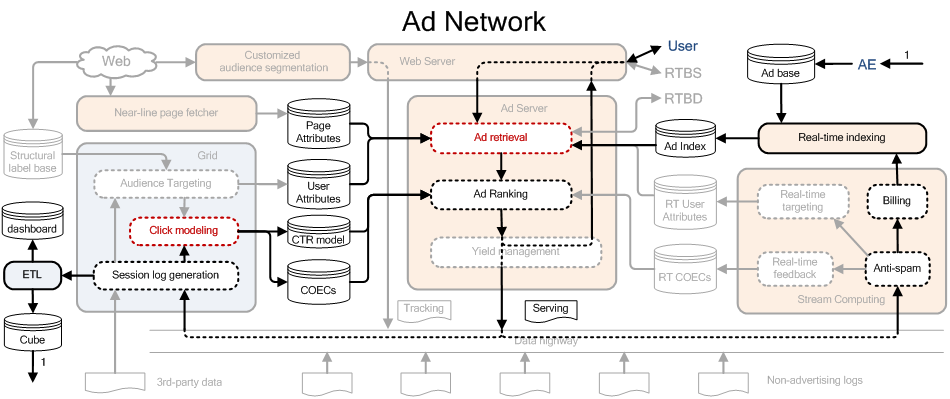

该架构的工作原理大致如下： 1. User 开始浏览某个页面时，Ad retrieval 根据 User 的 User Attributes 和页面的 Page Attributes 从 Ad Index 中找到相关的广告 (如果有广告主将广告新加进来时，也要通过 Real-time indexing 将广告加入 Ad Index 中) 2. 对相关广告根据 eCPM 进行排序，由于点击的 value 已经由广告主决定，这时只需要预估点击率即可。 3. 进行排序后需要将排序的结果及其用户后续的点击行为记录到日志中，从而便于改进点击率预估模型，同时通过流式计算平台进行反作弊监测以及对广告主收费（如果用户有点击行为的话）。

下面要介绍以上广告网络中提到的一些技术，

广告检索 (Ad Index)

规模较大的时候才用。检索是一种搜索技术，这里主要介绍两个重点：布尔表达式检索和长 Query 情况下的相关性检索。

布尔表达式检索 将每篇文档看做一个布尔表达式，同时将每个查询也看做一个布尔表达式。

如下面是一个表示文档的布尔表达式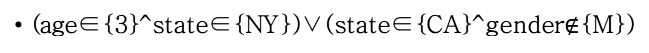

只有当文档满足查询的布尔表达式条件时，才能出这个广告，为了加快这个检索过程，布尔表达式检索通过建立两层索引来实现加速。其涉及到的一些概念和具体方法如下 (摘自 PPT）

长 Query 情况下的相关性检索指的是当查询的布尔表达式中的条件较多时，如果采用传统的搜索引擎的搜索方法，会导致计算量非常大，这里提供的思路是：在查找候选文档的过程中做一个近似的评估，切掉那些理论上不需要再考虑的文档，只对进候选的文档进行相关性计算，比 Top-N 最小堆最小值大的插入

采用的具体算法是 WAND 算法，其细节如下（摘自 PPT）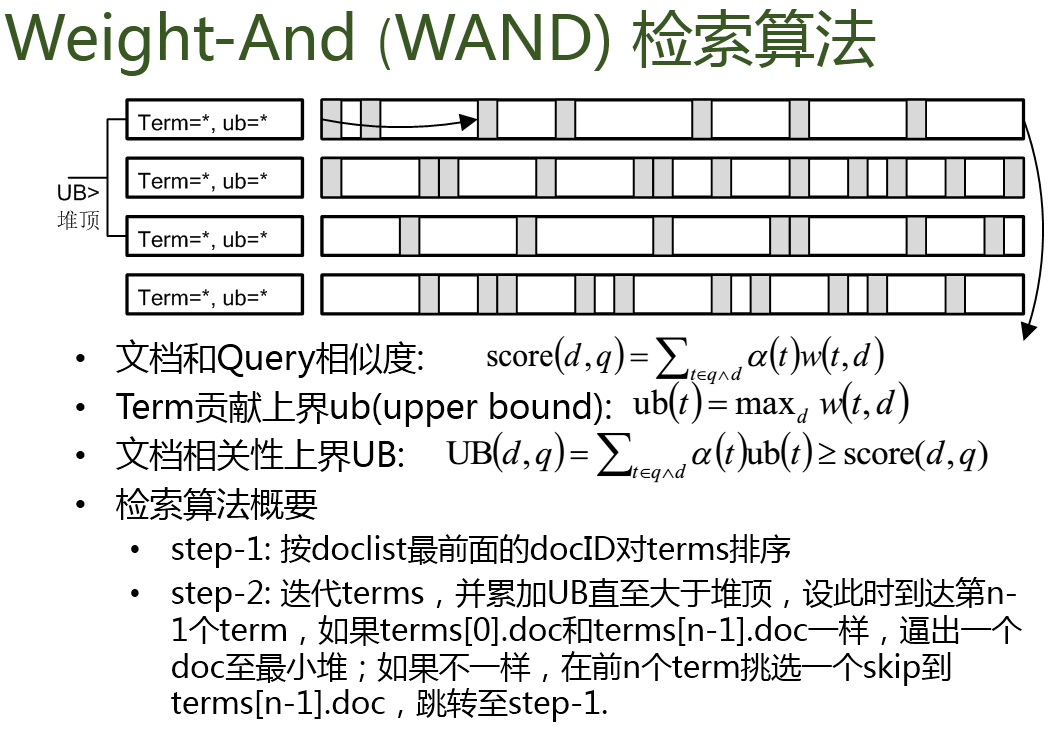

一致性问题

Zookeeper

Zookeeper 是在基于消息传递通信模型的分布式环境下解决一致性问题的基础服务

用层次式 Namespace 维护同步需要的状态空间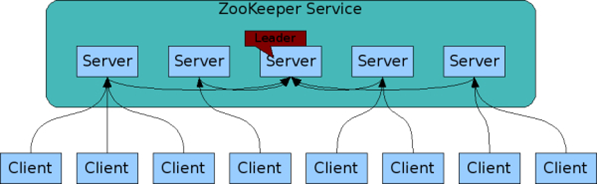

保证实现特性：Sequential Consistency, Atomicity, Single System Image, Reliability, Timeliness，较复杂的同步模式需要利用 API 编程实现。Zookeeper 的实现利用了 Paxos 算法。

Paxos 算法概念

目的是解决分布式环境下，怎么分布式地决策某些状态使得所有机器都处于一致性。

节点角色： P (roposer): (提出提案 (n, value)), A (cceptor), L (earner)

三个约束： 1. value 只有在被提出后才能被批准 2. 在一次算法的执行实例中，只批准一个 value 3. learners 只能获得被批准的 value

准备阶段 1. P 选择某提案编号 n 并将 prepare 请求发给 A 中的某多数派； 2. A 收到消息后，若 n 大于它已经回复的所有消息，则将自己上次接受的提案回复给 P，并承诺不再回复小于 n 的提案；

批准阶段： 1. 当 P 收到了多数 A 回复后，进入批准阶段。它要向回复请求的 A 发送 accept 请求，包括编号 n 和根据约束决定的 value 2. 在不违背向其他 P 的承诺的前提下，A 收到请求后即接受。

点击率预测

从广告检索出相关的广告后，需要根据 eCPM 对相关广告进行排序，由于出价由广告主决定，因此实际中需要估算的往往是广告的点击率。

基于统计的模型

\[\begin{align} u(a,u,c) = p(click|a,u,c) \end{align}\]

在这个问题上，Regression 比 Ranking 合适一些，因为广告的实际排序是根据 eCPM，而 eCPM 由点击率和出价相乘决定，因此需要尽可能准确估计 CTR，而不仅仅是各候选的 CTR 排序正确

冷启动问题：指的是新的广告非常多，这种情况下利用广告层级结构 (creative, solution, campaign, advertiser)，以及广告标签对新广告点击率做估计

捕获点击率的动态特性，两种方案：动态特征: 快速调整特征在线学习：快速调整模型

逻辑回归

逻辑回归是工程中常用的点击率预估方法。

动态特征

在线广告的三个维度 $(u,a,c)$ 上均有不同的特征，可以通过组合这些特征构造高纬特征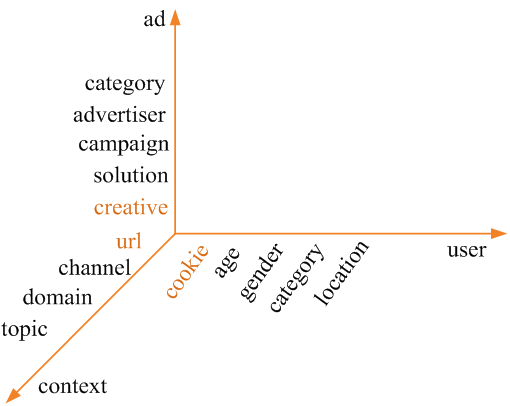

上面的组合特征均为静态特征，如果在这些组合的静态特征上加上这个特征的历史数据就变成了动态特征，和某个静态特征为 “年龄为 25~35 且为男性”，如果这个特征的取值为在某段时间的下单量而不是单纯的 0 或 1，那么这个特征就是一个动态特征。因此动态特征即在标签组合维度上聚合点击反馈统计作为 CTR 预测的特征。

优势 1. 工程架构扩展性强，变 features 不变 model (与在线学习相比) 2. 对新 $(a, u, c)$ 组合有较强 back-off 能力

缺点 1. 在线特征的存储量大，更新要求高

组合维度举例:

cookie(u) and creative(a)
gender(u) and topic(c)
location(u) and advertiser(a)
Category(a) and category(u)
cookie(u)
creative(a)
gender(u)

优化方法

L-BFGS

基于梯度的方法在工程上的收敛性不好，因为工程上的问题总是病态的。用二阶的方法，一般用 Quasi-Newton 方法。

BFGS (Broyden, Fletcher, Goldfarb, and Shanno) 是 Quasi-Newton 方法的一种，思路为用函数值和特征的变化量来近似 Hession 矩阵，以保证正定性，并减少计算量。

BFGS 方法 Hession 计算公式如下 (空间复杂度为 $O(n^2)$ )：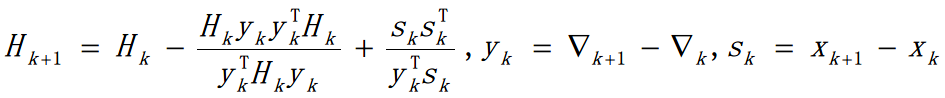

L (imited memory)-BFGS 是为了解决 BFGS 的空间复杂度问题。将 nxn 的 Hession 阵用下图方式加以近似 ($B_k$ 为 Hession 近似)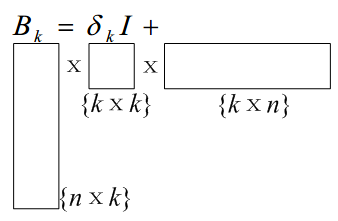

这样的方法将空间复杂度降为 $O(nk)$, 在特征量大时比 BFGS 实用

可以非常容易地用 map/reduce 实现分布式求解，这种方法也适用于梯度法：mapper 求部分数据上的梯度，reducer 求和并更新参数

ADMM

Alternating Direction Method of Multipliers 的形式

\[\begin{align}\min f(x)+g(z)\\\ s.t. Ax + Bz = c\end{align}\]

Augmented Lagrangian 及迭代解法如下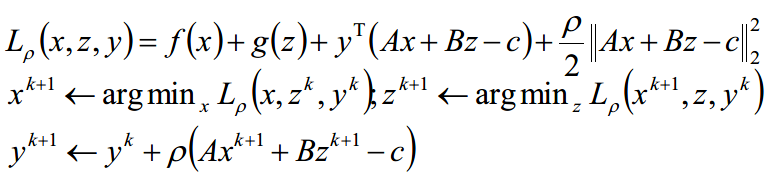

上面的迭代方法也可以用下面的迭代公式描述，其效果是一致的，但是下面的描述更加简便，而且在实际中也更常用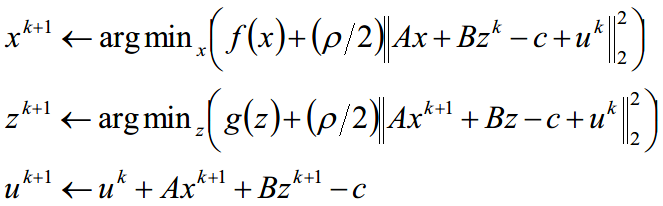

ADMM 这种迭代的解法能够很容易地通过 MapReduce 模式迭代进行求解。

下面介绍逻辑回归的 ADMM 分布式解法，这种方法将将样本划分为 N 份，每个 mapper 负责一份，其描述的最优化问题如下

\[\begin{align}\min \sum_{i=1}^{N}\sigma (w_ix_i)+r(z)\\\ s.t. w - z = 0\end{align}\]

分布式的迭代解法入下:

\[\begin{align}w_i^{k+1} \leftarrow \arg \min_{w_i} (\sigma(w_ix_i) + \frac{\rho}{2}||w_i - z^k + \mu_i^k||_2^2)\\\ z^{k+1} \leftarrow \arg \min_{z} (r(z) + \frac{N\rho}{2}||z^k - \overline w^{k+1}+ \overline \mu_k||_2^2)\\\ \mu_i^{k+1} \leftarrow \mu_i^k + w_i^{k+1} - z^{k+1} \end{align}\]

探索与利用 (Explore and exploit， E&E)

这一问题主要是为长尾的 $(a, u, c)$ 组合创造合适的展示机会以积累统计量，从而更准确地估计其 CTR

原因是真实的环境中，数据总是长尾的，总体集没法通过采样获得，实际上大批广告主的广告是没有机会展示，为了让更多的广告主的广告能够得到恰当的展示，需要做一些探索（即不选择当前出价最高的广告，而是选择一些符合要求的长尾广告），但是最终的目的仍是提升整体的广告收入，即需要严格控制探索的量和有效性

基本方法思路 1. 通常描述为 Multi-arm Bandit (MAB) 问题：有限个 arms (或称收益提供者) $a$, 每个有确定有限的期望收益 $E(r_{t,a})$ 2. 在每个时刻 t, 我们必须从 arms 中选择一个，最终目标是优化整体收益基本方法为 $\epsilon$–greedy: 将 $\epsilon$ 比例的小部分流量用于随机探索

上面的方法应用在广告中的主要挑战有：

海量的组合空间需要被探索
各个 arm 的期望收益是动态变化的

因此提出了以下两个思路， UCB 和 Contextual Bandit

UCB 在时刻 t，通过以往的观测值以及某种概率模型，计算每个 arm 的期望收益的 upper confidence bound (UCB)，并选择 UCB 最大的 arm。

实际上是将每个 arm 的收入看作一个分布，选择所有分布中可能达到最大的那个 arm 作为最终的选择。

我们不可能一直选择非最优的 arm, 原因是我们选择的此 arm 次数越多，其 UCB 就越接近于其期望收益

具体 UCB 策略有以下两种：

β-UCB 策略：依一个很大的概率，我们选择非最优 arms 的次数存在着一个上界，该上界与总的选择次数无关
UCB-tuned 策略：我们已选择的次数越多，就越可以自信地抛弃不太有前途 (但仍有可能最优) 的 arm.

Contextual Bandit

解决 arm 数目过多问题，降维，映射到另外的特征空间

对每次展示，每个 arm (广告) $a$ 有一个对应的特征矢量 $x(u,a)$
用此特征矢量代替 arm 本身进行 Bandit 决策