CTR 预估模型简介 -- 非深度学习篇

发表于 2018-07-15 标签计算广告，机器学习

本文主要介绍 CTR 预估中常用的一些模型，主要是非深度学习模型，包括 LR、GBDT+LR、FM/FFM、MLR。每个模型会简单介绍其原理、论文出处以及其一些开源实现。

LR(Logistic Regerssion)

LR + 海量人工特征 是业界流传已久的做法，这个方法由于简单、可解释性强，因此在工业界得到广泛应用，但是这种做法依赖于特征工程的有效性，也就是需要对具体的业务场景有深刻的认识才能提取出好的特征。

原理

LR 是一个很简单的线性模型，其输出的值可认为是事件发生 (\(y=1\)) 的概率，即输出值如下式所示

\[\begin{align} h(x) = p(y=1|x) = \sigma(w^Tx+b) \end{align}\]

其中 \(w\) 为模型参数，\(x\) 为提取的样本特征，两者均为向量，\(b\) 是偏置项。\(\sigma\) 为 sigmoid 函数，即 \(\sigma(x) = 1/(1+e^{-x})\)

有了事件发生的概率，则事件不发生的概率为 \(p(y=0|x) = 1-h(x)\), 将这两个概率通过如下一条公式表示为

\[\begin{align} p(y|x) = h(x)^y(1-h(x))^{1-y} \end{align}\]

有了这个概率值，则给定 \(n\) 个样本，便可通过极大似然估计来估算模型参数，即目标函数为

\[\begin{align} \max \prod_{i=1}^np(y_i|x_i) \end{align}\]

通常我们还会对概率取 log，同时添加负号将 max 改成 min，则可将目标函数改写成如下的形式

\[\begin{align} \min -\sum_{i=1}^ny_i\log h(x_i)+(1-y_i)\log (1-h(x_i)) \end{align}\]

上面的损失函数也叫作 log loss，实际上多分类的 cross entropy 也同以通过极大似然估计推导出来。

有了损失函数，便可通过优化算法来求出最优的参数，由于这是个无约束的最优化问题，可选用的方法很多，最常用的就是 gradient descent，除此之外，另外还有基于二阶导数的牛顿法系列，适用于分布式中的 ADMM，以及由 Google 在论文 Ad Click Prediction: a View from the Trenches 中提出的 FTRL 算法，目前也是业界普遍采用的方法，该算法具有 online learning 和稀疏性的良好特性，online learning 指的是其更新方式与 SGD (stochastic gradient descent) 相似，稀疏性指的是该算法能够解决带非光滑的 L1 正则项的优化问题。由于这里这篇文章主要讲述各种 CTR 预估模型，因此这里不对优化算法做展开了。

上面提到了 L1 正则项，就是在原来的损失函数基础上加上了 \(C\sum_{i=1}^m |w_i|\) 这一项，表示各个参数的绝对值的和乘上常数 \(C\)；加上这一项后能够使得最终的求解出来的参数中大部分的 \(|w_i|\) 为 0，这也是稀疏性的名称来源。稀疏性使得模型的复杂度下降，缓解了过拟合的问题，同时具有有特征筛选的能力。因为 LR 模型可以理解为对各个特征进行加权求和，如果某些特征的权重即 \(w_i\) 为 0，则可认为这些特征的重要性不高。在 CTR 预估中输入的是海量人工特征，因此添加 L1 正则化就更有必要了。

由于 L1 正则项不再是处处光滑可导的函数，因此在优化损失函数时。原来的 gradient descent 不能够直接使用，而是要通过 subgradient 的方法或前面提到的 FTRL 算法进行优化。

上面涵盖了 LR 模型的基本原理。而在 CTR 预估中，应用 LR 模型的重点在于特征工程。LR 模型适用于高维稀疏特征。对于 categorical 特征，可以通过 one-hot 编码使其变得高纬且稀疏。而对于 continious 特征，可以先通过区间划分为 categorical 特征再进行 one-hot 编码。同时还需要进行特征的组合 / 交叉，以获取更有效的特征。

一些问题

上面介绍过程中有一些结论我们直接就使用了，下面对于上面提到的某些结论做出一些解释

1. LR 的输出为什么可以被当做是概率值？

这部分涉及到广义线性模型 (GLM，Generalized linear model) 的知识，这里略过复杂的推导，直接给出结论。简单来说，LR 实际上是一个广义线性模型，其假设是二分类中 \((y|x,\theta)\) 服从伯努利分布 (二项分布)，即给定输入样本 \(x\) 和模型参数 \(\theta\), 事件是否发生服从伯努利分布。假设伯努利分布的参数 \(\phi\) ，则 \(\phi\) 可作为点击率。通过广义线性模型的推导，能够推出 \(\phi\) 的表示形式如下

\[\begin{align} \phi = 1/(1+e^{-\eta}) \end{align}\]

从上面的式子可知，LR 中的 sigmoid 函数并不是凭空来的，而式子中的 \(\eta\) 也被称为连接函数（Link function), 是确定一个 GLM 的重要部分，在 LR 中为简单的线性加权。

另外，如果将输出值与真实值的误差的分布假设为高斯分布，那么从 GLM 可推导出 Linear Regression，关于 GLM 详细的推导可参考这篇文章广义线性模型（GLM）。

2. 为什么 L1 正则项能够带来稀疏性？

这里有个很直观的回答，l1 相比于 l2 为什么容易获得稀疏解？，简单来说，就是当不带正则项的损失函数对于某个参数 \(w_i\) 的导数的绝对值小于 l1 正则项中的常数 \(C\) 时，这个参数 \(w_i\) 的最优解就是 0。

因为求解某个参数 \(w_i\) 使得损失函数取极小值时可分两种情况讨论 (下面的 \(L\) 为不带正则项的损失函数) 1）\(w_i<0\) 时，\(L+C|w_i|\) 的导数为 \(L'- C\) 2) \(w_i>0\) 时，\(L+C|w_i|\) 的导数为 \(L'+C\)

当 \(w_i<0\) 时，令 \(L'- C < 0\), 函数在递减；而当 \(w_i>0\) 时，令 \(L'+C > 0\), 函数在递增，则 \(w_i=0\) 便是使得损失函数最小的最优解，且结合 \(L'- C < 0\) 和 \(L'+C > 0\)，可得 \(C > |L'|\)。这便是我们上面得到的结论，上面是针对某一个参数，实际上也可以推广到所有参数上。事实上，通过 subgradient descent 求解这个问题时也能够得到相同的结论。

3. 连续特征为什么需要离散化？

参考这个问题：连续特征的离散化：在什么情况下将连续的特征离散化之后可以获得更好的效果？

离散化后有以下几个好处：

稀疏向量内积乘法运算速度快，计算结果方便存储
离散化后的特征对异常数据有很强的鲁棒性：比如一个特征是年龄 > 30 是 1，否则 0。如果特征没有离散化，一个异常数据 “年龄 300 岁” 会给模型造成很大的干扰；
逻辑回归属于广义线性模型，表达能力受限；单变量离散化为 N 个后，可以通过 one-hot 编码为每个变量设置单独的权重，相当于为模型引入了非线性，能够提升模型表达能力，加大拟合；
离散化后可以进行特征交叉，由 M+N 个变量变为 M*N 个变量，进一步引入非线性，提升表达能力；
特征离散化后，模型会更稳定，比如如果对用户年龄离散化，20-30 作为一个区间，不会因为一个用户年龄长了一岁就变成一个完全不同的人。当然处于区间相邻处的样本会刚好相反，所以怎么划分区间要取决于具体的场景

4.1 为什么要对 categorical 特征做 One-hot 编码后再输入 LR？

参考这篇文章 One-Hot 编码与哑变量，简单来说，就是 LR 建模时，要求特征具有线性关系，而实际应用中很少有满足这个假设关系的，因此 LR 模型效果很难达到应用要求。但是通过对离散特征进行 one-hot 编码，LR 可以为某个特征中所有可能的值设置一个权重，这样就能够更准确的建模，也就能够获得更精准的模型。而 one-hot 编码后特征实际上也是做了一个 min-max 归一化，能够克服不同特征的量纲差异，同时使模型收敛更快。

开源实现

由于 LR 模型的广泛性，基本上每个机器学习库或者框架都有相关实现，如 sklearn 提供了单机版的实现，spark 提供了分布式版本的实现，腾讯开源的 Parameter Server Angel 中也提供了 LR+FTRL 的实现，Angel 支持 Spark，目前也还在开发中。除此之外，Github 上也有很多个人开源的实现，这里不再列举。

LS-PLM(Large Scale Piece-wise Linear Model)

LS-PLM (也叫作 MLR, Mixture of Logistics Regression) 是阿里妈妈在 2017 年在论文 Learning Piece-wise Linear Models from Large Scale Data for Ad Click Prediction 中公开的，但是模型早在 2012 年就在阿里妈妈内部使用。这个模型在 LR 基础上进行了拓展，目的是为了解决单个 LR 无法进行非线性分割的问题。

原理

LR 是一个线性模型，模型会在数据空间中生成一个线性分割平面，但是对于非线性可分的数据，这一个线性分割面显然无法正确分割这些数据。以下图为例（摘自上面的论文），A）为一组非线性训练数据的正负样本分布；对于该问题，LR 会生成 B）中的分割平面，C) 图展示的 LS-PLM 模型则取得了较好的效果。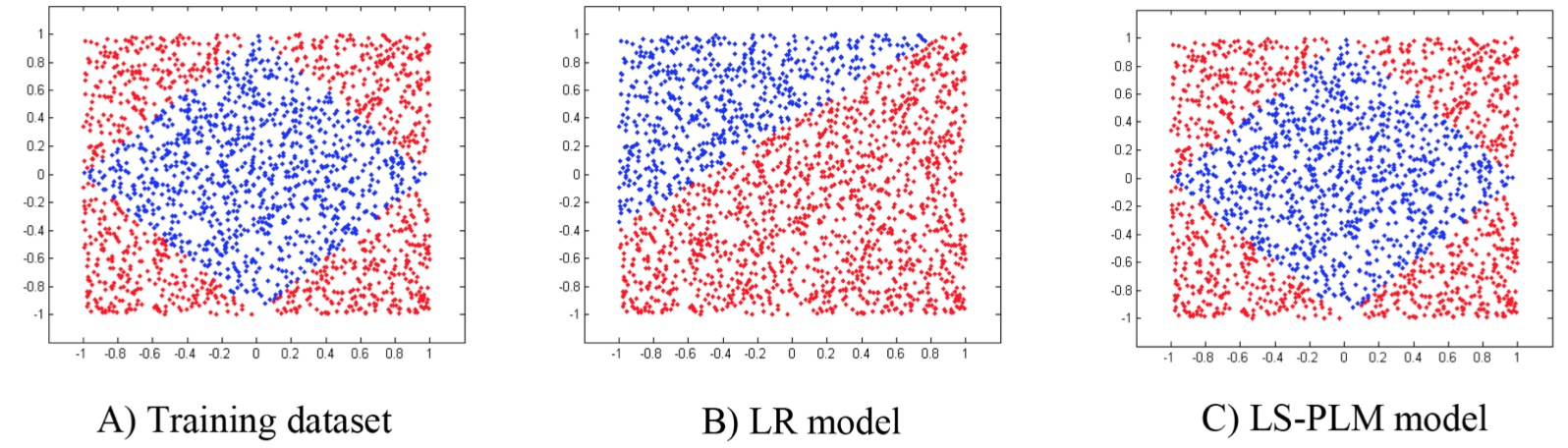

在 CTR 问题中，划分场景分别建模是一种常见的手法。例如，同一产品的 PC/APP 端，其用户的使用时间和习惯差异可能很大；比如 PC 可能更多是办公时间在看，而手机则是通勤时间或者临睡前使用更多。假设有 hour 作为特征，那么 “hour=23” 对于 APP 端更加有信息量，而对于 PC 可能意义不大。因此，区分 PC/APP 端分别建模可能提升效果。

LS-PLM 也是采用这个思想的，不够这里不是划分场景，而是划分数据，通过将数据划分不同的 region、然后每个 region 分别建立 LR。

这里需要注意的是这里一个样本并不是被唯一分到了一个 region，而是按权重分到了不同的 region。其思想有点像 LDA (Latent Dirichlet allocation) 中一个单词会按照概率分到多个 topic 上。

论文中的公式如下

\[\begin{align} p(y=1|x) = g ( \sum_{j=1}^m \sigma(\mu_j^T x)\eta(w_j^Tx)) \end{align}\]

公式中的符号定义如下：

参数定义如下：

\(m\) : region 的个数 (超参数：一般是 10~100)
\(\Theta=\{\mu_1,\dots,\mu_m, w_1,\dots,w_m \}\): 表示模型的参数，需要训练
\(g(\cdot)\)：为了让模型符合概率定义 (概率和为 1) 的函数
\(\sigma(\cdot)\)：将样本分到 region 的函数
\(\eta(\cdot)\)：在 region 中划分样本的函数

前面提出的公式更像个框架，在论文中，只讨论了 \(g(x) = x\), \(\sigma\) = softmax ，\(\eta\) = sigmoid 的情形，而且因此，上面的公式可写成如下的形式

\[\begin{align} p(y=1|x) = \sum_{i=1}^m \frac{e^{\mu_i^Tx}}{\sum_{j=1}^m e^{\mu_j^Tx}}\frac{1}{1+e^{-w_i^Tx}} \end{align}\]

这个公式其实已经变成了通过多个 LR 模型进行加权求和的 bagging 模式，只是这里每个模型的权重是学习出来而不是事先确定的。

写出了概率函数，后面的推导跟前面的 LR 其实是一样的，也是先通过极大似然估计得到 \(\max\) 问题，添加负号后转为损失函数求 \(\min\) 问题。这里不做详细的推导了。

在 LS-PLM 中也是需要添加正则项的，除了在 LR 中提到的 L1 正则化，论文还提出了 \(L_{2,1}\) 正则项，表示如下

\[\begin{align} ||\Theta||_{2,1} = \sum_{i=1}^d \sqrt {\sum_{j=1}^m(\mu_{ij}^2+w_{ij}^2)} \end{align}\]

上式中的 \(d\) 表示特征的维数，其中 \(\sqrt {\sum_{j=1}^m(\mu_{ij}^2+w_{ij}^2)}\) 表示对某一维特征的所有参数进行 L2 正则化，而外侧的 \(\sum_{i=1}^d\) 表示对所有的 feature 进行 L1 正则化，由于开方后的值必为正，因此这里也不用添加绝对值了。由于结合了 L1 和 L2 正则项，所以论文也将这个叫做 \(L_{2,1}\) 正则项。

由于损失函数和正则项都是光滑可导的，因此优化方面比带 L1 正则的 LR 更加简单，可选的优化方法也更多。

MLR 适用的场景跟 LR 一样，也是适用于高纬稀疏特征作为输入。

开源实现

前面提到的腾讯的 PS Angel 实现了这个算法，具体可参考这里；Angel 是用 Scala 开发的。也有一些个人开源的版本如 alphaPLM，这个版本是用 C++ 写的，如果需要实现可以参考以上资料。

GBDT+LR(Gradient Boost Decision Tree + Logistic Regression)

GBDT + LR 是 FaceBook 在这篇论文 Practical Lessons from Predicting Clicks on Ads at Facebook 中提出的，其思想是借助 GBDT 帮我们做部分特征工程，然后将 GBDT 的输出作为 LR 的输入。

原理

我们前面提到的无论 LR 还是 MLR，都避免不了要做大量的特征工程。比如说构思可能的特征，将连续特征离散化，并对离散化的特征进行 One-Hot 编码，最后对特征进行二阶或者三阶的特征组合 / 交叉，这样做的目的是为了得到非线性的特征。但是特征工程存在几个难题：

连续变量切分点如何选取？
离散化为多少份合理？
选择哪些特征交叉？
多少阶交叉，二阶，三阶或更多？

而 GBDT + LR 这个模型中，GBDT 担任了特征工程的工作，下面首先介绍一下 GBDT。

GBDT 最早在这篇论文 Greedy Function Approximation：A Gradient Boosting Machine 中提出； GBDT 中主要有两个概念：GB (Gradient Boosting) 和 DT (Decision Tree)，Gradient Boosting 是集成学习中 boosting 的一种形式，Decision Tree 则是机器学习中的一类模型，这里不对这两者展开，只讲述在 GBDT 中用到的内容。关于决策树的介绍可参考这篇文章决策树模型 ID3/C4.5/CART 算法比较。

在 GBDT 中采用的决策树是 CART (Classification And Regression Tree)，将其当做回归树使用，这里的回归树是一棵在每个树节点进行分裂的时候，给节点设定其在某个特征的的值，若样本对应的特征的值大于这个给定的值的属于一个子树，小于这个给定的值的属于另一个子树。

那么，构建 CART 回归树是的关键问题就在于选择具体的特征还有这个特征上具体的值了。选择的指标是平方误差最小化准则。对于任意一个切分，其平方误差计算方式如下

假设切分后左子树有 \(m\) 个样本，右子树有 \(n\) 个
计算左子树样本的目标值的均值为 \(y_m = \frac{1}{m}\sum_{i=1}^{m}y_i\), 同样计算右子树样本的目标值的均值为 \(y_n = \frac{1}{n}\sum_{j=1}^{n}y_j\)
平方误差和为 \(L = \sum_{i=1}^m(y_i - y_m)^2 + \sum_{j=1}^n(y_j - y_n)^2\)
对于每一个可能的切分值，我们都可计算其平方误差和 \(L\)，选择使得 \(L\) 最小的切分点即可。

上面便是 GBDT 中的 “DT” 部分，用于解决一个回归问题，也就是给定一组样本，我们可以通过上面的方式来构建出一棵 CART 来拟合这组样本。下面我们来讲一下 GBDT 中的 “GB” 部分。

简单来说，gradient boosting 就是将若干个模型的输出进行叠加作为最终模型的输出。如下图是一个简单的例子 (图片来源于提出 xgb 的论文：XGBoost: A Scalable Tree Boosting System)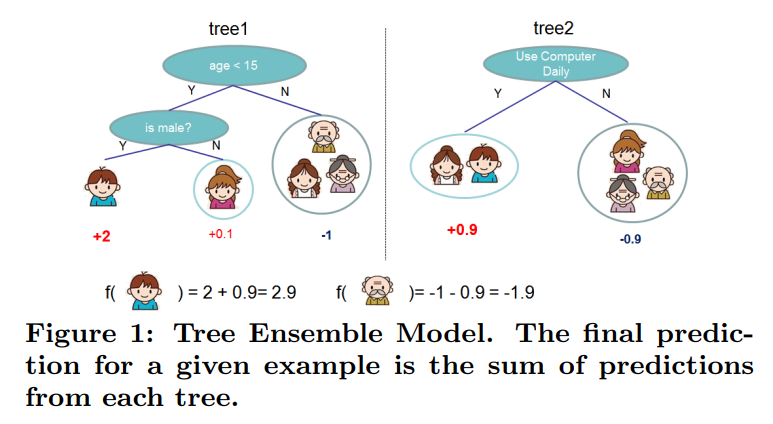

下式就是叠加了 \(T\) 个 \(f_t(x)\) 模型作为最终的模型，\(f_t(x)\) 在 GBDT 中就是一棵 CART，当然 \(f_t(x)\) 不限于树模型。

\[\begin{align} F(x) = \sum_{t=1}^Tf_t(x) \end{align}\]

在构建每棵树的时候，输入的样本不同的地方在于每个样本的目标值 \(y\)；如构建第 \(k\) 棵树，对于原始样本 \((x_i, y_i)\), 其目标值变为

\[\begin{align} y_{ik} = y_i - \sum_{t=1}^{k-1}f_t(x_i) \end{align}\]

即输入第 \(k\) 棵树的样本变为 \((x_i, y_{ik})\)，所以在构建第 \(k\) 棵树的时候，实际上是在拟合前 \(k-1\) 棵树的输出值的和与样本真实值的残差。

回到我们的 GBDT + LR 模型，首先通过前面提到的 GBDT 训练出一批树模型，然后样本输入每棵树后最终都会落到一个具体的叶子节点上，那我们就将这个节点标为 1，其他叶子节点标为 0，这样每棵树输出的就相当于是一个 one-hot 编码的特征。如下图是摘自 FaceBook 原始论文的图，里面有两棵树，假如输入 \(x\) 在第一棵树中落入第一个叶子节点，在第二棵树种落入第二个叶子节点，那么输入 LR 的特征为 [1, 0, 0, 0, 1].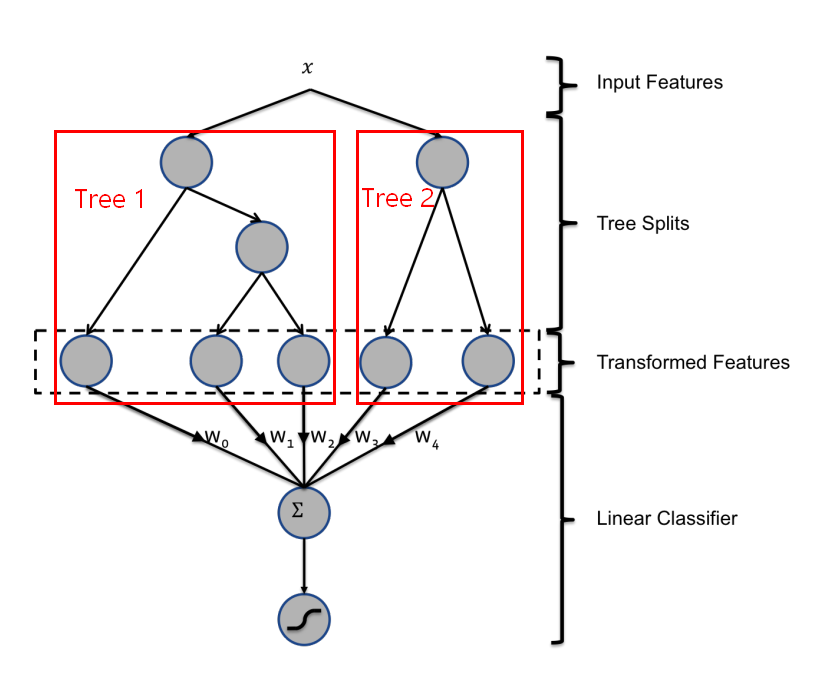

GBDT+LR 方案中每棵决策树从根节点到叶节点的路径，会经过不同的特征，此路径就是特征组合，而且包含了二阶，三阶甚至更多，因此输出的 one-hot 特征是原始特征进行交叉后的结果。而且每一维的特征其实还是可以追溯出其含义的，因为从根节点到叶子节点的路径是唯一的，因此落入到某个叶子节点表示这个特征满足了这个路径中所有节点判断条件。

GBDT 适用的问题刚好与 LR 相反，GBDT 不适用于高纬稀疏特征，因为这样很容易导致训练出来的树的数量和深度都比较大从而导致过拟合。因此一般输入 GBDT 的特征都是连续特征。

在 CTR 预估中，会存在大量的 id 特征，对于这种离散特征，一般有两种做法 1) 离散特征不直接输入到 GBDT 中进行编码，而是做 one-hot 编码后直接输入到 LR 中即可；对于连续特征，先通过 GBDT 进行离散化和特征组合输出 one-hot 编码的特征，最后结合这两种 one-hot 特征直接输入到 LR。大致框架如下所示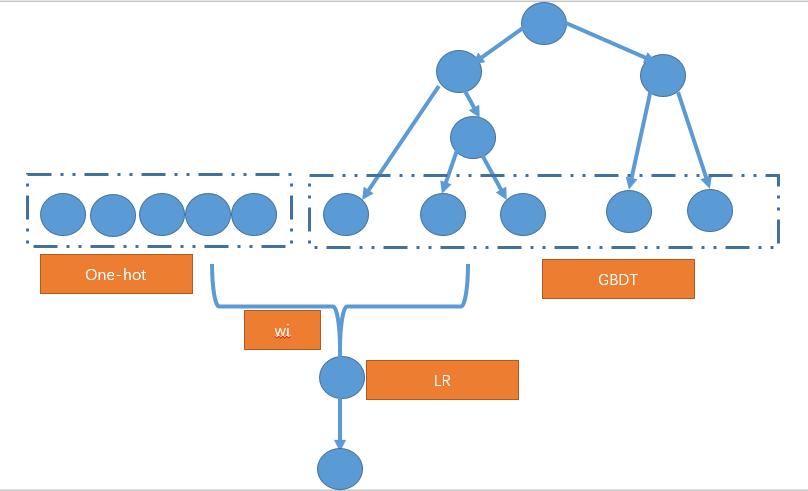

将离散的特征也输入 GBDT 进行编码，但是只保留那些出现频率高的离散特征，这样输入 GBDT 中的 one-hot 特征的维度会遍地，同时通过 GBDT 也对原始的 one-hot 特征进行了组合和交叉。

一些问题

1. GBDT 中的 gradient 在哪里体现了？

推导到现在，好像也没有提及到 gradient，其实前面拟合残差时已经用到了 gradient 的信息。

首先，我们要转换一下思维，我们一般在优化中使用的 gradient descent 都是对某个参数进行的，或者说是在参数空间中进行的，但是除了参数空间，还可以在函数空间中进行。如下图所示对比了两种方式 (下面两张图均摘自 GBDT 算法原理与系统设计简介)

在函数空间中，是对函数直接进行求导的，因此 GBDT 算法的流程如下

上图中的 \(\tilde{y_i}\) 就是我们前面说的第 \(i\) 个样本的残差，当损失函数为平方损失即 \[L(y,F(x)) = \frac{1}{2}(y-F(x))^2\]

对 \(F(x)\) 求导得出的残差为

\[\begin{align} \tilde{y_i} = y_i - F(x_i) \end{align}\]

这正是我们前面说的样本的真实值与前面建的树的输出和的差。如果损失函数改变，这个残差值也会进行相应的改变。

2. GBDT 怎么处理分类问题？

上面我们讲的 GBDT 是处理回归问题的，但是对于 CTR 预估这一类问题，从大分类上其实还是一个分类问题。那 GBDT 是怎么处理这个问题？

在回归问题中，GBDT 每一轮迭代都构建了一棵树，实质是构建了一个函数 \(f\)，当输入为 x 时，树的输出为 \(f(x)\)。

在多分类问题中，假设有 \(k\) 个类别，那么每一轮迭代实质是构建了 \(k\) 棵树，对某个样本 \(x\) 的预测值为 \(f_{1}(x), f_{2}(x), ..., f_{k}(x)\),

在这里我们仿照多分类的逻辑回归，使用 softmax 来产生概率，则属于某个类别 \(j\) 的概率为

\[\begin{align} p_{c} = \frac{\exp(f_{j}(x))}{ \sum_{i=1}^{k}{exp(f_{k}(x))}} \end{align}\]

通过上面的概率值，可以分别计算出样本在各个分类下的 log loss，根据上面 GBDT 在函数空间的求导，对 \(f_1\) 到 \(f_k\) 都可以算出一个梯度，也就是当前轮的残差，供下一轮迭代学习。也就是每一轮的迭代会同时产生 k 棵树。

最终做预测时，输入的 \(x\) 会得到 \(k\) 个输出值，然后通过 softmax 获得其属于各类别的概率即可。

更详细的推导可参考这篇文章：当我们在谈论 GBDT：Gradient Boosting 用于分类与回归

开源实现

直接实现 GBDT + LR 的开源方案不多，但是由于两者的耦合关系并不强，因此可以先训练 GBDT，然后将原始特征通过 GBDT 转换后送入到 LR 中，GBDT 有多个高效的实现，如 xgboost，LightGBM。

FM(Factorization Machine)

FM（Factorization Machine）是于 2010 年在论文 Factorization Machines 中提出，旨在解决稀疏数据下的特征组合问题。其思想是对组合特征的参数所构成的参数矩阵进行矩阵分解，从而得到每个原始特征的隐向量表示，更新特征的隐向量对数据的稀疏性具有鲁棒性。关于 FM 和 FFM ，美团点评这篇文章：深入 FFM 原理与实践其实已经写得很详细了，本文主要参考该文章进行修改。

原理

FM 可以认为是在 LR 的基础上加入特征的二阶组合，即最多有两个特征相乘，则模型可表示成如下形式

\[\begin{align} y(\mathbf{x}) = w_0+ \sum_{i=1}^n w_i x_i + \sum_{i=1}^n \sum_{j=i+1}^n w_{ij} x_i x_j \end{align}\]

从模型也可以看出，其实 FM 是在 LR 基础上增加了最后的二阶交叉项。

从上面的公式可以看出，组合特征的参数一共有 \(\frac{n(n−1)}{2}\) 个，任意两个参数都是独立的。然而，在数据稀疏性普遍存在的实际应用场景中，二次项参数的训练是很困难的，原因是每个参数 \(w_{ij}\) 的训练需要大量 \(x_i\) 和 \(x_j\) 都非零的样本；由于样本数据本来就比较稀疏，满足 \(x_i\) 和 \(x_j\) 都非零的样本将会非常少。训练样本的不足，则会导致参数 \(w_{ij}\) 不准确，最终将严重影响模型的性能。

如何解决这个问题？FM 中借鉴了矩阵分解的思想，在推荐系统中，会对 user-item 矩阵进行矩阵分解，从而每个 user 和每个 item 都会得到一个隐向量。如下图所示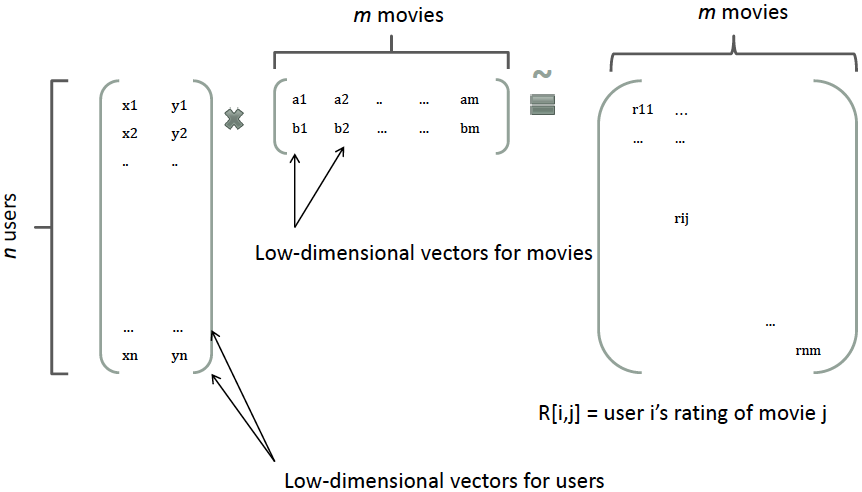

类似地，所有二次项参数 \(w_{ij}\) 可以组成一个对称阵 \(W\)，那么这个矩阵就可以分解为 \(W=V^TV\)，\(V\) 的第 \(j\) 列便是第 \(j\) 维特征的隐向量。换句话说，每个参数可表示成两个隐向量的内积的形式。即 \(w_{ij}=<v_i,v_j>\)，\(v_i\) 表示第 \(i\) 维特征的隐向量，这就是 FM 模型的核心思想。因此，可以将上面的方程改写成如下形式

\[\begin{align}y(\mathbf{x}) = w_0+ \sum_{i=1}^n w_i x_i + \sum_{i=1}^n \sum_{j=i+1}^n <v_i, v_j>x_i x_j \end{align}\]

假设隐向量的长度为 \(k(k<<n)\)，二次项的参数数量减少为 \(kn\) 个，远少于多项式模型的参数数量。另外，参数因子化使得 \(x_hx_i\) 的参数和 \(x_ix_j\) 的参数不再是相互独立的，因此我们可以在样本稀疏的情况下相对合理地估计 FM 的二次项参数。

具体来说，\(x_hx_i\) 和 \(x_ix_j\) 的系数分别为 \(<v_h,v_i>\) 和 \(<v_i,v_j>\)，它们之间有共同项 \(v_i\)。也就是说，所有包含 \(x_i\) 的非零组合特征（即存在某个 \(j≠i\)，使得 \(x_ix_j≠0\)）的样本都可以用来学习隐向量 \(v_i\)，这很大程度上避免了数据稀疏性造成的影响。而在多项式模型中，\(w_{hi}\) 和 \(w_{ij}\) 是相互独立的。

另外，原始论文还对特征交叉项计算的时间复杂度做了优化，具体见如下公式

\[\begin{align} \sum_{i=1}^n \sum_{j=i+1}^n \langle \mathbf{v}_i, \mathbf{v}_j \rangle x_i x_j = \frac{1}{2} \sum_{f=1}^k \left(\left( \sum_{i=1}^n v_{i, f} x_i \right)^2 - \sum_{i=1}^n v_{i, f}^2 x_i^2 \right) \end{align}\]

从公式可知，原来的计算复杂度为 \(O(kn^2)\)，而改进后的时间复杂度为 \(O(kn)\)

在 CTR 预估中，对 FM 的输出进行 sigmoid 变换后与 Logistics Regression 是一致的，因此损失函数的求解方法以及优化算法都基本一致，这里不再详细展开。

由于 FM 可以看做是 LR 基础上加上二阶特征组合的模型，同时模型本身对稀疏性有较好的鲁棒性，因此 FM 适用范围跟 LR 一样，都适用于输入的特征是高纬度稀疏特征。

开源实现

FM 在 github 上有单机版本的开源实现 fastFM和 pyFM， fastFM 是一个学术项目，发表了相关论文 fastFM: A Library for Factorization Machines, 对 FM 进行了拓展；同时我们前面提到的腾讯的 PS Angel 中也实现了这个算法，可参考这里。

FFM(Field-aware Factorization Machine)

FFM 发表于论文 Field-aware Factorization Machines for CTR Prediction，是台大的学生在参加 2012 KDD Cup 时提出的，这个论文借鉴了论文 Ensemble of Collaborative Filtering and Feature Engineered Models for Click Through Rate Prediction 中的 field 的概念，从而提出了 FM 的升级版模型 FFM。

原理

通过引入 field 的概念，FFM 把相同性质的特征归于同一个 field。简单来说，同一个 categorical 特征经过 One-Hot 编码生成的数值特征都可以放到同一个 field，包括用户性别、职业、品类偏好等。

在 FFM 中，每一维特征 \(x_i\)，针对其它特征的每一种 field \(f_j\)，都会学习一个隐向量 \(v_{i,f_j}\)。因此，隐向量不仅与特征相关，也与 field 相关。也就是说，假设有 \(f\) 个 field，那么每个特征就有 \(f\) 个隐向量，与不同的 field 的特征组合时使用不同的隐向量，而原来的 FM 中每个特征只有一个隐向量。

实际上，FM 可以看作 FFM 的特例，是把所有特征都归属到一个 field 时的 FFM 模型。根据 FFM 的 field 敏感特性，同样可以导出其模型方程如下

\[\begin{align} y(\mathbf{x}) = w_0 + \sum_{i=1}^n w_i x_i + \sum_{i=1}^n \sum_{j=i+1}^n \langle \mathbf{v}_{i, f_j}, \mathbf{v}_{j, f_i} \rangle x_i x_j \end{align}\]

其中，\(f_j\) 是第 \(j\) 个特征所属的 field。如果隐向量的长度为 \(k\)，那么 FFM 的二次参数有 \(nfk\) 个，远多于 FM 模型的 \(nk\) 个。此外，由于隐向量与 field 相关，FFM 二次项并不能够化简，其预测复杂度是 \(O(kn^2)\)。

其实，FFM 是在 FM 的基础上进行了更细致的分类，增加了参数的个数使得模型更复杂，能够拟合更复杂的数据分布。但是损失函数的推导以及优化的算法跟前面的 FM 还有 LR 都是一样的，因此这里不再赘述。

FFM 适用的场景跟 FM 和 LR 一样，适用于输入的特征是高维稀疏特征。

开源实现

FFM 最早的开源实现是台大提供的 libffm，去年开源的 xlearn 中也提供了该算法的实现，提供的 api 比 libffm 更加友好。

另外，由于 FM/FFM 可以看做是 LR 加了特征交叉的增强版本，对输入的特征的特点要求一致，因此上面的 GBDT+LR 也可以直接套到 GBDT+FM/FFM 上，值得一提的是，还是台大的学生，在 2014 由 Criteo 举办的比赛上，通过 GBDT+FFM 的方案夺冠，其实现细节可参考 kaggle-2014-criteo。

小结

在非深度学习中，可以看到主流的几个模型基本都是基于 LR 进行的拓展或将 LR 与其他模型结合。原因是 LR 模型简单，具有良好的理论基础，可解释性强，能够获取各个特征的重要性，且能够直接输出概率值。但是应用 LR 过程中无法避免且最为重要的一点就是人工特征工程，特征决定了上限，虽然 FM/FMM 和 GBDT+LR 在一定程度上起到了自动特征工程的作用，但是需要人工特征还是占主要部分。

后面要讲的深度学习的方法在一定程度上能够缓解这个问题，因为深度学习能够通过模型自动学习出有效特征，因此，深度学习也被归类为表示学习 ( Representation Learning) 的一种；但是，没有免费午餐的，特征工程的便利性带来的是特征的不可解释性，所以怎么选取还是要根据具体的需求和业务场景。