《Smart Pacing for Effective Online Ad Campaign Optimization》阅读笔记
《Smart Pacing for Effective Online Ad Campaign Optimization》是 Yahoo 在 2015 发表的一篇关于 budget pacing 的论文,与之前写过的 Budget Pacing for Targeted Online Advertisements at LinkedIn 相似,目标也是把预算均匀花完,但是除了这个目标,这篇论文还提出了在预算均匀花完的基础上如何保成本的方法,算是一个多目标优化了。在离线环境和真实环境验证了方法的有效性,是实践性较强的一篇文章,值得一看。
背景
预算控制的做法目前可分为两大流派:Probabilistic throttling 和 Bid modification,其中 Probabilistic throttling 通过一个概率值 (下图中的 Pacing Rate) 来决定是否计划参竞来控制预算花费速率,而 Bid modification 则通过直接改价的方式来控制花费速率。两种方式的简单区别如下图所示,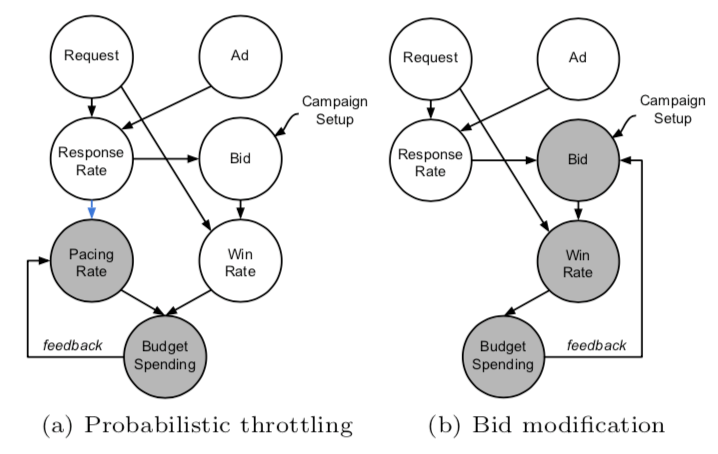
本文使用的方法属于第一种方式即 Probabilistic throttling,文章说这么做主要原因有以下三个
- Probabilistic throttling 是直接影响 budget 花费的速度,而 Bid modification 则是通过改变 win rate 间接达到影响 budget 花费的速度的,这种方式有可能导致 budget 花费波动较大
- bid landscape (即广告投放中的一些统计信息,能够反映投放的竞争情况,更详细可参考 Bid Landscapes 和 DSP 的 bidding 算法) 一般会随着时间变化而变化;以上两点使得通过 Bid modification 来达到 budget pacing 比较困难
- 使用 Probabilistic throttling 时能够将 pacing control 与 bid optimization 解耦,能够分别进行优化
虽然文章是这么列出这三点优点,但是笔者觉得其中有个很大的问题:就是不进行 bid modification 时,假如当前的 bid 太小,即使 pacing rate 调到了 1 也拿不到任何的 impression 时 预算岂不是花不出去?
文章提到说 bid 有单独的一个 bid optimization module 也许能解决这个额问题,但是并没有详细展开这个 module 是如何工作的,是否能够解决上面的问题。
这篇 paper 以及 Budget Pacing for Targeted Online Advertisements at LinkedIn 都是通过 Probabilistic throttling 进行 budget pacing 的,而通过 bid modification 进行的 budget pacing 的 paper 也不少,可以参考以下两篇
- Optimal delivery of sponsored search advertisements subject to budget constraints
- Dynamics of bid optimization in online advertisement auctions
算法流程
这部分主要描述文章是如何对问题进行建模和近似求解,主要思想是对一个计划的不同 request 分层(根据 ctr,cvr 等),在不同的分层采用不同的 pacing rate;并且根据实时的花费效果调整 pacing rate,根据是否需要优化效果,算法又分成了 Campaigns without Performance Goals 和 Campaigns with Performance Goals
问题建模
文章里主要解决两大类问题,第一类是只让计划均匀花完预算即可,第二类则需要在预算均匀花完基础上保住点击成本 (eCPC), 对应的方法在文章中称为 Campaigns without Performance Goals 和 Campaigns with Performance Goals,下面会分别介绍。
文章约定了一些符号以便对问题进行建模
- \(r_i\): 在第 \(i\) 个请求参竞的概率,就是本文描述的 pacing rate, \(s_i \sim Bern(r_i)\) 则表示是否参竞这个事件
- \(w_i\):赢得第 \(i\) 个请求的概率
- \(c_i\): 赢得第 \(i\) 个请求的 cost
- \(p_i\): 在第 \(i\) 个请求能带来用户点击等行为的概率,\(q_i \sim Bern(p_i)\) 则表示是否带来点击这个事件
通过上述符合可定义
\(C = \sum_i s_iw_ic_i\) 为计划的总 cost
\(P = \frac{C}{\sum_i s_i w_i q_i}\) 为计划的 performance, 即成本(如点击成本,转化成本等), 文中描述为 eCPC 即点击成本
此外,计划在一天的总预算 \(B\) 和总 cost \(C\) 都会被划分到 K 个时间片内,以此来度量 budget pacing 的效果;即 \(B = \sum_{t=1}^{K}B^{(t)}\), \(C = \sum_{t=1}^{K}C^{(t)}\),则 budget pacing 的 error 定义如下
\[\begin{align} \Omega(B, C) = \sqrt{\frac{1}{K}\sum_{t=1}^{K}(C^{(t)}-B^{(t)})^2} \end{align}\]
则对第一类问题即只需要 pacing 预算的问题文章建模如下
\[\begin{align} \min_{r_i} P \\\ s.t\quad C = B, \Omega(C, B) \le \epsilon \end{align}\]
上面的 \(\epsilon\) 表示可容忍的 pacing 误差,总体表示在满足预算均匀花完时最小化成本即 \(P\)
上面建模中一个值得注意问题是最小化成本是否合理?由于文章是 DSP 视角出发进行建模的,从仅考虑广告主的利益角度来说,最小化成本是合理的;但是对于一个完整的广告系统即 SSP,ADX 和 DSP 都在同一个平台时,这并不适用;如微信、抖音、微博等 app 的广告,SSP、ADX 和 DSP 往往都由这个 app 所在的公司运作,如果一味的最小化成本会损害平台的利益,因此更合理的做法是尽可能让广告主的真实成本与其预期成本接近
而对于第二类不仅需要 pacing 预算同时需要保证 performance 的问题,文章建模如下
\[\begin{align} \min_{r_i} \Omega(C, B) \\\ s.t\quad P \le G, B-C \le \epsilon \end{align}\]
上面的 \(G\) 表示广告主的目标成本,其他符号含义与前面描述一致,表示在广告主成本不超和预算花费不超的情况下,让预算更 pacing 地花完。
问题求解
文章对两种问题提出了两种上面建模,但是在实际求解时并没有对上面这两个最优化问题进行求解,而是通过启发式方法 (heuristics) 近似求解这个问题, 这个启发式方法其实就是一个控制算法, 而至于为什么启发式方法能够近似求解上面的最优化问题,文章并没有说明。
文章的一个亮点是对一个广告计划的所有 requests 做分层,分层的依据是 request 在这个计划的 ctr,而不同的 pacing rate 是不一样的,当一个 request 到来的时候,先判断这个 request 属于哪一个层,然后再取出这个层对应的 pacing rate 作为最终的 pacing rate;ctr 越高的层,其对应的 pacing rate 就越大
而每个层的 pacing rate 会在固定时间间隔进行调整,调整的方法就是下文要介绍的两个控制算法。
Campaigns without Performance Goals
这部分的控制算法针对的问题是第一类问题即只需要保证 budget 被 pacin'g
根据上面的分层方法,假设每个广告计划的所有 requests 会被分成 \(L\) 层,则在第 t-1 个时间片内各层的 pacing rate 记为 \(r^{(t-1)} = (r_1^{(t-1)}, r_2^{(t-1)}...r_L^{(t-1)})\), 且各层的 cost 记为 \(c^{(t-1)} = (c_1^{(t-1)}, c_2^{(t-1)}...c_L^{(t-1)})\)
前面提到一天的总预算 \(B\) 会根据时间片划分成 \(K\) 份小预算,即 \(B = (B^{(1)}, B^{(2)}....B^{(K)})\), 但是实际花费中不能保证每个时间片的 cost 都刚好达到分配的预算值,因此如果前面的时间片中出现了少投或超投情况,就要把少投或超投那些部分均摊到后面的时间片中,所以每个时刻的预算需要根据前面的花费来调整,记的经过调整的预算为 \(\hat{C}^{(t)}\),则 \(\hat{C}^{(t)}\) 可表示为
\[\begin{align} \hat{C}^{(t)} = B^{(t)} + \frac{B_m - \sum_{i=t}^KB^{(i)}}{K-m} \end{align}\]
上式中的 \(B_m\) 表示经过了 \(m\) 个时间片后剩余的实际预算,分母 \(B_m - \sum_{i=t}^KB^{(i)}\) 表示当前预算花费是否超过了预期 (<0) 或者不满足预期 (>0),并通过分母均摊到后面的 \(K-m\) 个时间片中。
则调整 \(L\) 个的 pacing rate 的控制算法如下图所示,图中的 \(R = \hat{C}^{(t)} - C^{(t-1)}\), 表示如果按照前一时间片的 pacing rate 即 \(r^{(t-1)}\) 投放时,当前时间片的预算 \(\hat{C}^{(t)}\) 能否花完。则当 \(R > 0\) 时,需要提高当前时间片的 pacing rate,反之需要降低 这一时间片的 pacing rate
上面的算法认为 pacing rate 的大小即 \(r^{(t)}\) 与实际的 cost 即 \(c^{(t)}\) 是成正比的,因此调整 pacing rate 也会根据 cost 的变化比例来调整
除此之外,上面算法还有几点细节需要注意
- \(l'\) 层表示 pacing rate 为非 0 的最小的层
- 当需要提升 pacing rate 时,是从第 \(L\) 层到 \(l'\) 层进行的;而需要降低 pacing rate 时,是从第 \(l'\) 层到第 \(L\) 层进行的,其目的都是优先提升 ctr 高的层的 pacing rate,优先降低 ctr 低的层的 pacing rate,从而达到上面最小化成本的目的
- trial rate 的目的令 pacing rate 非 0 的最小层的下一层以一个很小的 pacing rate 进行参竞(pacing rate 会随着层数增加而增加),目的是后面预算花费加速做准备, trail rate 在这里是一个超参,是一个很小的值,后面会介绍该如何选取
Campaigns with Performance Goals
这部分的控制算法除了要保证 budget 被 pacing 花完,还要保证成本小于预设的成本;而每一层的成本在这里记为 \(e = (e_1, e_2...e_L)\), 其中 \(e_i = \frac{CPM}{1000*p_i}\)
考虑了成本的算法在主要在上面的算法上增加了一个 ExpPerf 函数,用于计算当前所有层的联合期望成本,该函数的定义如下
\[\begin{align} ExpPerf(c^{(t-1)}, r^{(t-1)}, r^{(t)}, e, i) = \frac{\sum_{j=i}^{L} \frac{c_j^{(t-1)} r_j^{(t)}}{r_j^{(t-1)}}}{\sum_{j=i}^{L} \frac{c_j^{(t-1)} r_j^{(t)}}{r_j^{(t-1)}e_j}} \end{align}\]
上面的式子中的分子可理解为各层在当前时间片的 cost 之和,分母可理解为各层在当前时间片的点击数之和,因此总体就是当前的时间片所有层的联合期望成本
则成本约束的 budget pacing 控制算法过程如下所示
如果计算出当前的联合期望成本大于目标成本时,会从第 1 层到第 L 层逐渐减少每层的 pacing rate,而这分为两种情况
- 如果当前层到第 L 层的联合期望成本大于目标成本,则当前层的 pacing rate 会直接置为 0;
- 如果当前层到第 L 层的联合期望成本不大于目标成本,当前层的 pacing rate 会根据上面算法第 7 行来调整,然后算法就终止了,根据文章描述其含义是调整当前的层使得总体的期望成本达到目标的期望成本;
但是文章并没具体解释第七行的公式的含义,比如说如分母为 0 时,\(r_{l}^{(t)}\) 岂不是变为无穷大?
超参选取
上面提过的算法的流程中涉及到多个超参数,如层数 \(L\) 以及 trial rate,下面介绍如何选取这两个超参
对于一个新计划,决定其层数 \(L\) 的方法如下,首先找到与这个新计划最相似的老计划 \(a\), 并找到这个老计划最合适的 pacing rate \(r_G\), 则新计划的层数可计算为 \(L = \lceil \frac{1}{r_G} \rceil\), 计算的逻辑其实就是要找到这个计划最合适 pacing rate 粒度对应的层数。
一旦层数决定后,在第一个时间片内会每个层都会通过 \(r_G\) 初始化,在第一个时间片积累了数据后,后面会根据上面提到的算法调整各层的 pacing rate。
前面提到 trail rate 的目的令 pacing rate 非 0 的最小层的下一层以一个很小的 pacing rate 进行参竞,因为 pacing rate 会随着层数增加而增加,本来这一层的 pacing rate 应该是 0 的,但是这里给了一个很小的 trail rate,目的是为了让后面加快预算花费做准备。其设置方法如下
将当前时间片的预算 \(\hat{C}^{(t)}\) 划分一小部分,记为 \(\lambda\)(e.g. \(\lambda\) = 1%), 假设当前层为第 \(l\) 层,则其 trail rate = \(r_l^{(\*)} ×\frac{\lambda ×\hat{C}^{(t)}}{c_l^{(\*)}}\) ,而 \(r_l^{(\*)}\) 和 \(c_l^{(\*)}\) 则是 \(l\) 层的历史 pacing rate 和 cost。
实验效果
文章对提出的方法进行了 AB 实验评估,并与论文 Budget Pacing for Targeted Online Advertisements at LinkedIn 中的方法进行了比较,预算的花费时间定义为一天,而时间片定义为 15 分钟;超参的值为 \(r_G = 0.01\) 以及 \(\lambda = 1\%\)
考察的指标主要有三个 1)performance 2)budget spending 3)spending pattern
而作为对比的 baseline 方法也是使用本文的方法,只是只有一层,下面是选取的三个计划进行 AB 测试的效果,实验组的层数为 8;其中计划 1 和 3 是没有 performance 目标也就是成本约束的,而计划 2 的 ecpc 为 2.5,从结果来看也能较好地满足成本约束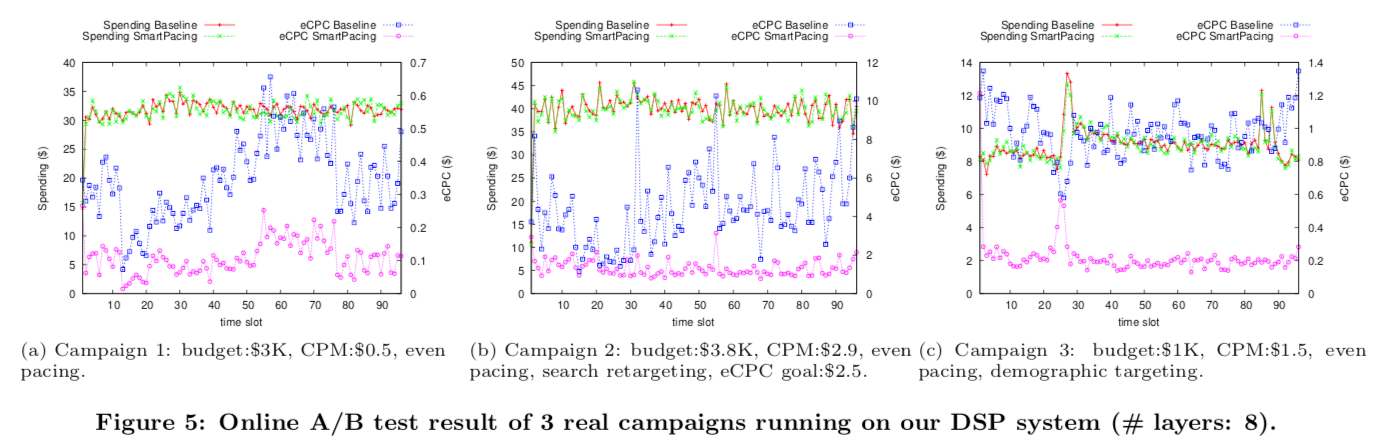
除此之外,还对比了两种方法在保证成本约束的效果,结果如下图所示,从结果来看,分层处理后能够有效降低成本,同时花费不变
同时文章与另外一篇论文 Budget Pacing for Targeted Online Advertisements at LinkedIn 中的 budget pacing 方法进行了对比,结果如下所示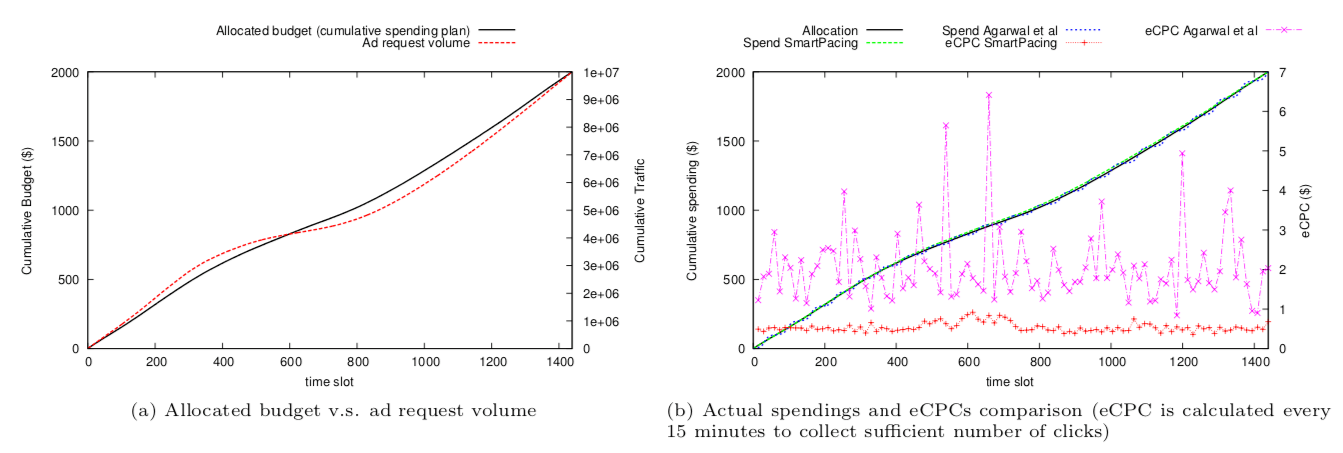
从结果来看,相比于 Budget Pacing for Targeted Online Advertisements at LinkedIn 中的方法,这篇文章调节 budget 的花费得更为平缓,同时成本的控制也更好,因为 Budget Pacing for Targeted Online Advertisements at LinkedIn 论文中的方法没有考虑成本问题。
工程实现
本文的方法的工程实现架构如下图所示,架构不复杂,左边的部分通过 message queue (如 kafka) 搜集后验数据,用于更新 in-memory data source 中各层的 pacing rate;右边的 Controller 则会利用 in-memory data source 中的 pacing rate 进行 budget pacing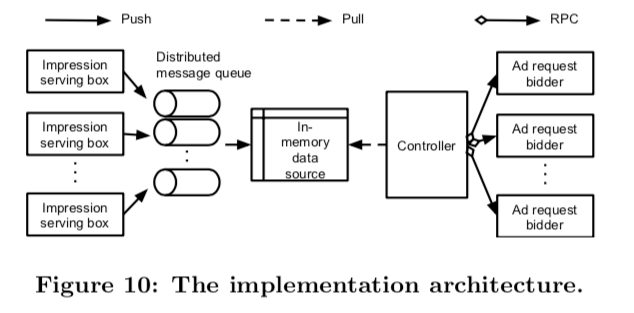
因为 pacing rate 是存储在内存中,存在丢失问题,因此会根据 message queue 中的日志进行恢复,其原理看起来跟 redis 的 AOF 模式恢复类似。
小结
这篇文章主要提出了两个基于 Probabilistic throttling 的算法用于解决 budget pacing 问题, 第一个算法仅解决了如何让预算更平缓地花完,第二个算法在第一个算法的基础上,不仅让预算平缓花完,还能保成本。文章中的方法的一个亮点在于根据 ctr 等指标将 request 分层,不同的层采用不同的 pacing rate,从而能够针对 ctr 高的 request 给予更高的 pacing rate,而这也是文章中的算法能够优化 performance 的原因。