《Modeling Delayed Feedback in Display Advertising》 阅读笔记
在计算广告中,转化是有延迟的,即在点击发生后过一段时间用户可能才会发生转化,且往往转化漏斗越深,延迟的时间越长;因此在训练 cvr/deepcvr 模型时,会有两种情况出现(1)过早把样本送入模型,把最终会转化但是还没回传 label 的事件当做负例,导致模型低估(2)过晚把样本送入模型,即让所有样本都等待一个足够长的时间才送入模型,导致模型没能及时更新
因此在建模时需要对转化的回传延时进行建模,这篇 paper 《Modeling Delayed Feedback in Display Advertising》是 criteo 针对这个问题提供的一个解决方法,主要思想就是对于还未观察到 conversion 的样本,不直接将其当做负样本,而是当前考虑 click 已发生的时间长短给模型不同大小的 gradient;paper 里称在 criteo 的真实的数据上验证了该方法的有效性。此外,文章从问题的建模到求解的思路不错,值得一看。
为什么要对延迟建模
与转化的回传紧密相关的一个话题就是归因(attribution),即将转化归到哪一个 click 上,paper 中用了常用的 last-click 归因,归因窗口固定在 30 天内,即在点击后 30 天以内回传的转化才认为是有效的。
对回传延迟建模往往要先分析延迟的分布,且对于不同的广告主、行业等,这个值的差异往往还是比较大的,在 paper 中统计结果如下图一所示,结果显示约 35% 的转化会在一小时内回传,50% 会在 24 小时内回传。
此外,paper 中还提到了新计划的问题,主要的观点是每天都会有大量的新计划被创建(如下图二所示),如果不能尽快将这些新计划对应的样本喂给模型,会导致模型在这些新计划上预估得不好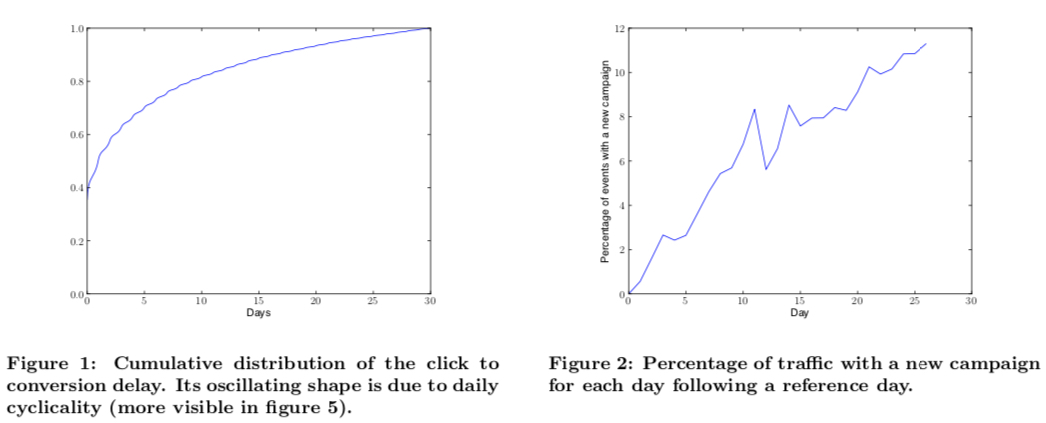
上面这两张图正好对应着文章开头说的要对 delayed conversion 进行建模的原因;图一表明如果样本不延迟做归因,会把最终会转化但是还没回传 label 的事件当做负例,导致模型低估,图二则表明如果等待过长时间才把样本送入模型,即让所有样本都等待一个足够长的时间才送入模型,会导致模型没能及时更新
问题建模
下面的建模采用到的一些符号及其含义如下所示
- \(X\): 特征
- \(Y \in \lbrace 0, 1\rbrace\): 当前时刻 conversion 是否已经发生了
- \(C \in \lbrace 0, 1\rbrace\):conversion 最终是否会发生
- \(D\):回传延迟的真正时间
- \(E\):当前已过去的时间
则当前如果
- 观察到转化还没发生即 \(Y=0\),有两种可能
- 转化最终不会发生 \(C=0\)
- 转化最终会发生,但是 \(D>E\)
- 观察到转化已发生即 \(Y=1\), 则肯定有 \(C=1\);即 \(Y=1\) 是 \(C=1\) 的充分条件
且 paper 中做了如下的假设,当前已过去的时间 \(E\) 与最终是否的转化时间以及是否会转化无关,即
\[\begin{align} P(C,D|X,E) = P(C,D|X) \end{align}\]
这个假设也是比较合理的,因为最终是否转化及转化的延迟时间与当前已经过去的时间长短无关。
paper 中对将问题分为两部分来建模,第一部分是常见的 ctr 预估模型,如下公式 (1) 所示,第二部分是通过指数分布来建模回传延迟 \(D\), 如下公式 (2) 所示;除了指数分布,weibull 分布、gamma 分布、log-normal 分布 也常被用来建模事件发生的时间间隔,这些分布是 Survival analysis 这个研究领域里常用的分布。
\[\begin{align} P(C=1|X=x)=p(x)=\frac{1}{1+\exp(-w_cx)} \tag{1} \end{align}\]
\[\begin{align} P(D=d|X=x, C=1)=\lambda(x)\exp(-\lambda(x)d) \tag{2} \end{align}\]
其中 \(\lambda(x)\) 在 survival analysis 中被称为 hazard function,其含义表示的是事件发生的频率 / 强度 ; 如对于指数分布,如果这个值越大,表示事件发生频率越大,事件间的时间间隔越短,则概率密度函数会越陡峭,如下图所示。此外,为了保证 \(\lambda(x) \gt 0\), 这里令 \(\lambda(x) = \exp(w_dx)\)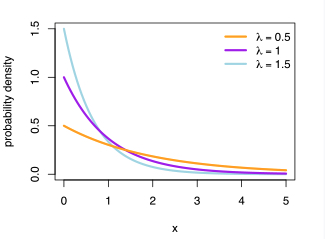
此外,指数分布用来建模两个事件发生的时间间隔,而泊松分布则用来建模某段时间里事件发生的次数,详细的讲解可参考知乎上的这个回答 指数分布公式的含义是什么?
有了公式 (1) 和公式 (2) 后,我们就可以推导在考虑回传延迟下 pvr 预估问题了;下面可分两种情况写出样本的似然:即已观察到 conversion 的样本和未观察到 conversion 的样本
已观察到 conversion 的样本的似然
即当前观察到 conversion 的概率可写成
\[\begin{align} \begin{split} p_1&=p(Y=1, D=d_i|X = x_i, E=e_i) \\\ &= p(Y=1,D=d_i|X = x_i) \\\ &= p(C=1,D=d_i|X = x_i) \\\ &= p(D=d_i|X=x_i, C=1)*p(C=1|X=x_i) \end{split} \end{align}\]
上面的推导的三步主要利用了以下三点
- 针对该问题的假设:当前已过去的时间 \(E\) 与最终是否会转化无关,同时与转化时间无关
- \(Y=1\) 是 \(C=1\) 的充分条件
- 条件概率公式 \(p(a|b,c) * p(b|c) = p(a,b|c)\)
最后可将概率表示成公式 (1) 和公式(2)的乘积,则
\[\begin{align} p_1=p(Y=1, D=d_i|X = x_i, E=e_i)=\lambda(x_i)\exp(-\lambda(x_i)d_i) * p(x_i) \tag{3} \end{align}\]
未观察到 conversion 的样本的似然
同理,可写出当前还没观察到 conversion 的样本的概率 \(p_0\) 为
\[\begin{align} \begin{split} p_0&=p(Y=0|X = x_i, E=e_i) \\\ &=p(Y=0|C=0, X = x_i, E=e_i)p(C=0|X=x_i) +\\\ &p(Y=0|C=1, X = x_i, E=e_i)p(C=1|X=x_i) \\\ &=p(C=0|X=x_i) + p(Y=0|C=1, X = x_i, E=e_i)p(C=1|X=x_i) \end{split} \end{align}\]
上面的推导的两步主要利用了以下两点
- 全概率公式 + 条件概率
- \(p(a|c)=\sum_{b_i}p(ab_i)\)
- \(p(ab_i|c)=\sum_{b_i}p(a|b_i, c)p(b_i|c)\)
- \(p(Y=0|C=0, X = x_i, E=e_i)=1\)
则上面的推导关键点在于求出条件概率 \(p(Y=0|C=1, X = x_i, E=e_i)\), 该条件概率的含义是当前未观察到 conversion 的样本最终会转化的概率,换种描述就是最终的延时 \(D\) 大于当前已过去时间 \(E\) 的概率,即可表示成如下公式
\[\begin{align} \begin{split} &p(Y=0|C=1, X = x_i, E=e_i) \\ &=p(D>E|C=1,X=x_i, E=e_i) \\ &=\int_{e_i}^{\infty} \lambda(x)\exp(\lambda(x)t)dt \\ &=\exp(-\lambda(x)e_i) \end{split} \end{align}\]
即最终有 \[p_0=p(Y=0|X = x_i, E=e_i)=1-p(x_i) + p(x_i) * \exp(-\lambda(x_i)e_i) \tag{4}\]
小结
综上
- 对于当前观察到 conversion 的样本,其似然函数为公式 (3) 即,
\[\begin{align} p_1=\lambda(x_i)\exp(-\lambda(x_i)d_i) * p(x_i) \end{align}\]
- 对于当前未观察到 conversion 的样本,其似然函数为公式 (4) 即
\[\begin{align} p_0=1-p(x_i) + p(x_i) * \exp(-\lambda(x_i)e_i) \end{align}\]
可以看到,这里 \(p_0 + p_1 \ne 1\), 跟我们常见的建模方式不一样
问题求解
上面的问题的解法的基本原理是 MLE (极大似然估计),但是根据是否显式地写出变量 \(C\) 的条件概率有两种解法,第一种是将 \(C\) 当做隐变量,通过 EM 算法求解;第二种没有直接写出隐变量 \(C\) 的概率密度函数,而是直接写出样本集的 likelihood,因为从上面的问题建模中已经基于当前观察到的 \(y_i\) 写出对应的似然函数了。
EM 算法
关于 EM 算法的推导,CS229 的讲义 EM algorithm 里讲得比较详细了,证明的基本流程就是
- 在似然函数中通过全概率公式引入隐变量
- 通过 Jensen’s inequality 把隐变量提出来
- 优化目标转转为最大化 Jensen’s inequality 的下界,让 Jensen’s inequality 取等号得到隐变量的概率密度函数 (E-step)
- 将隐变量的概率密度函数带入似然函数中做 MLE 即可 (M-step)
知乎上也有一个比较通俗的回答人人都懂 EM 算法,因此证明过程这里就不再展开赘述了
简单来说,EM 算法中的 E-step 是为了通过条件概率 \(p(z|x;\theta)\) 来表示隐变量 \(H\),从而替换掉似然函数中的隐变量;进而在 M-step 中只针对 \(\theta\) 来进行进行极大似然即可. 如下图所示是 CS229 讲义里的一次迭代的流程,里面的 \(i\) 表示隐变量可能的状态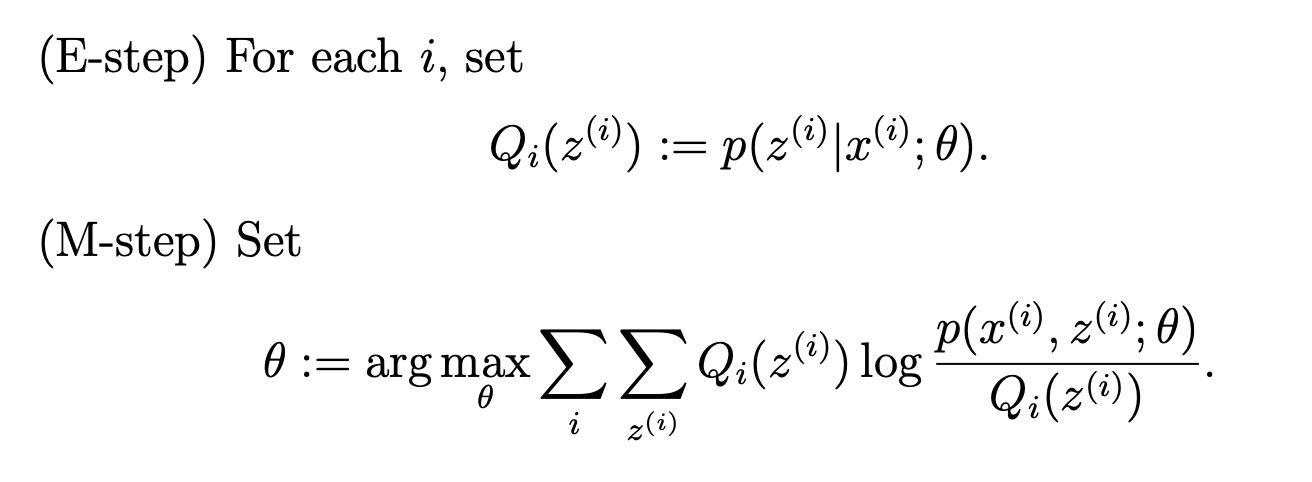
EM 算法的证明中通过证明了算法会随着 E-step + M-step 逐步收敛的,但是不能保证收敛到全局最优,如果我们的优化目标是凸的,则 EM 算法可以保证收敛到全局最优,因为对于凸函数局部最优即全局最优。
回到这个问题,由于 \(C\) 是隐变量,则 E-step 和 M-step 的过程分别如下
E-step
给定一个样本 \((x_i, y_i, e_i)\), 令隐变量的条件概率为
\[\begin{align} p(C=1|X=x_i, Y=y_i) := w_i \end{align}\]
相比于上面的 EM 算法的流程,我们这还多了一个 \(y_i\), 因此还要对 \(y_i\) 的值进行分类讨论
- 当 \(y_i=1\) 时,可知 \(w_i=1\)(因为 \(Y=1\) 是 \(C=1\) 的充分条件)
- 当 \(y_i=0\) 时,其计算方法如下, 即
\[\begin{align} \begin{split} w_i&=p(C=1|Y=0,X=x_i,E=e_i) \\\ &=p(Y=0|C=1, X = x_i, E=e_i)p(C=1|X=x_i) \\\ &=p(x_i) * \exp(-\lambda(x_i)e_i) \end{split} \end{align}\]
计算出 \(w_i=p(C=1|X=x_i, Y=y_i)\) 后,\(p(C=0|X=x_i, Y=y_i) = 1-w_i\)
M-step
M step 最大化的似然函数根据 \(Y\) 和 \(C\) 的值可分为四项,分别对应与上图中 M-step 中的两层 \(\sum\) 嵌套,且在 \(Y=1\) 的情况下 \(C=0\) 的概率为 0,最终 M-step 的似然函数如下所示
\[\begin{align} \begin{split} L&=\sum_{i,y_i=1}w_i \* \log p(Y=1,D=d_i|X=x_i,E=e_i) + \\\ &\sum_{i,y_i=0}[ w_i \* \log p(Y=0,C=1|X=x_i,E=e_i) + \\\ &(1-w_i) \* \log p(Y=0,C=0|X=x_i,E=e_i)] \end{split} \end{align}\]
且由前面可知,\(w_i\) 取值为
\[\begin{align} w_i = \begin{cases} 1 & &y_i =1 \\\ p(x_i) * \exp(-\lambda(x_i)e_i) & &y_i =0 \end{cases} \end{align}\]
因此,利用公式 (3) 和公式 (4) 的推导,导入上式最终化简得到结果为
\[\begin{align} \begin{split} L&=\sum_{i}w_i \log p(x_i) + (1-w_i) \log(1-p(x_i)) \\\ &+\sum_{i} \log(\lambda(x_i))y_i - \lambda(x_i)t_iw_i \end{split}\tag{5} \end{align}\]
除了 \(w_i\) 的值要根据 \(y_i\) 的值变化外,公式 (5) 中的 \(t_i\) 也需要根据 \(y_i\) 的值变化,即如下所示
\[\begin{align} t_i = \begin{cases} e_i &y_i =1 \\\ d_i &y_i =0 \end{cases} \end{align}\]
至此,可通过公式 (5) 对 \(p\) 和 \(\lambda\) 进行 MLE 了,且从公式 (5) 中可看到,对 \(p\) 执行的优化是一个 weighted logistics regression 的过程,而对 \(\lambda\) 执行的优化构成则是一个 exponential regression
Joint Optimization
在上面的问题建模中,基于当前观察到的 \(y_i\) 已经能写出样本对应的似然函数了,因此虽然问题中包含隐变量 \(C\), 但是不一定要显示的将 \(C\) 的条件概率写出来(当无法写出样本对应的似然函数了需要这一步,这个时候就一定要通过 EM 算法求解了)
根据 MLE,求解的问题可表示成如下形式
\[\begin{align} \arg \min_{w_c,w_d} L(w_c,w_d)+\frac{\mu}{2}(||w_c||_2^2 + ||w_d||_2^2) \end{align}\]
上面的公式中加入了 L2 regularization,要求教的 \(w_c,w_d\) 分别是 \(p\) 和 \(\lambda\) 的参数;根据公式 (3) 和 (4), 可写出 \(L(w_c,w_d)\) 为
\[\begin{align} L(w_c,w_d) = -\sum_{i, y_i=1} \log(p(x_i)+ \log \lambda(x_i)-\lambda(x_i)d_i - \\\ \sum_{i, y_i=0} \log[1-p(x_i) + p(x_i) \exp(-\lambda(x_i)e_i)] \end{align}\]
其中,\(p(x)=\frac{1}{1+\exp(-w_cx)}\) , \(\lambda(x) = \exp(w_dx)\)
则对 \(w_c\) 和 \(w_d\) 的导数如下图所示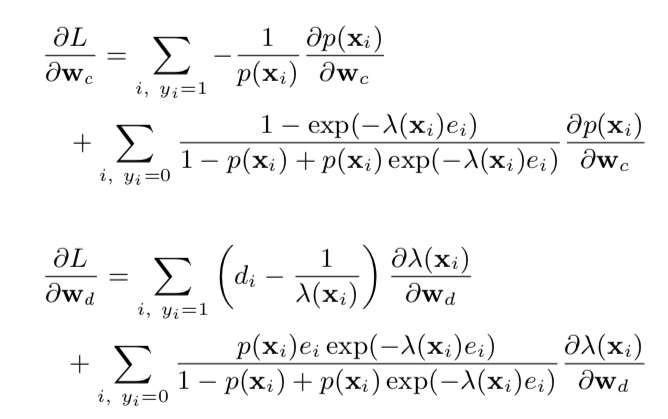
从上面的求导的表达式可知,对于当前 \(y_i=0\) 即 label 还没回传的样本,其对 \(w_c\) 的影响可从下面两方面去了解
(1) 当 \(\lambda(x_i)e_i \ll 1\), 即当前已经过去的时间 \(e_i\) 远小于平均的回传时间 \(\lambda(x_i)^{-1}\) 时,\(\sum_{i, y_i}\) 这一项几乎为 0,表示 click 发生的时间还很短,没法完全确认最终是没有 conversion 的 (2)\(\lambda(x_i)e_i \gg 1\), 即当前已经过去的时间 \(e_i\) 远大于平均的回传时间 \(\lambda(x_i)^{-1}\) 时,对 \(w_c\) 贡献的梯度是 \(1/(1-p(x_i))\), 相当于在 logistics regression 中的一个负样本的梯度,表示已经过了较长时间还没观察到 conversion,可认为这个样本是负样本了
小结
前面主要讲了求解建模好的问题的两种解法,第一种方法是显式地写出了隐变量 \(C\) 的条件概率,并通过 EM 算法求解;第二种方法则是直接写出所有样本的似然函数直接求解。值得注意的是,在 serving 的时候只使用 ctr 预估模型,而不用建模延时的指数回归模型,因为在做反向传播过程中已经考虑了回传延迟对参数进行了修正
实验
实验数据:实验数据使用了 criteo 里的真实数据(但是 paper 里附的实验数据链接打不开了);7 天测试数据,每天的测试数据对应的训练数据是其前 3 周的数据(约 600w 条样本)
实验设置:为了与实验提出来的 DFM 模型作对比,对照组里提供了若干个模型
- Short Term Conversion (STC): 采用了两个模型
- 第 1 个模型用来预估样本在某段时间内转化的概率,即 \(p(C=1,D \le 1 day|X=x)\)
- 第 2 个模型用来预估在这段时间内转化的样本占所有转化样本的比例,即 \(p(D \le 1 day|C=1, X=x) = p(C=1,D \le 1 day|X=x)/p(C=1|X=x)\)
- 则最终预估的概率是 \(p(C=1|X=x)=\), 即是上面两个模型预估值之比
- NAIVE: 不考虑样本的转化的回传延迟
- SHIFTED:所有样本都等待 30 天后,确认每个样本的 label 都是准确后才把模型送入样本进行训练
- ORACLE: 拥有上帝视角的模型,即在样本送入模型时就能知道这个样本最终是否会转化
- RESCALE:与 NAIVE 一样,但是预估的 cvr 会除以一个常数,
实验结果如下图所示,评估指标是平均 negative log-likelihood(NLL),因为 NLL 比起 AUC 等指标更能反映预估 cvr 值的准确性。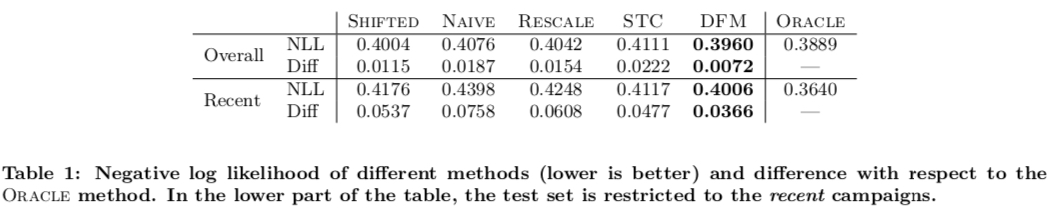
实验中提供了两套评估数据集,overall 和 recent,前者是全集,后者则是专门针对新计划的,从实验结果来看,DFM 模型的预估结果次优于有上帝视角的 ORACLE 模型。
小结
综上,paper 针对转化回传有延迟的问题提出了一种建模方法,建模的思想是不把还没观察到 conversion 的样本直接当做负样本去处理,而是考虑其距离当前 click 发生的时间长短给予模型不同权重的梯度。
除了之外,这个问题另一种思路就是直接用 regression model 来建模回传延迟的时间。而转化回传的延迟除了会影响 cvr 模型的预估,还会影响以保成本为目标的 bidding 方式,即当前 conversion 还没回传时,不能直接认为没有 conversion,而是要考虑一种更为平滑的 pacing 策略。