程序的表示、转换与链接 - week2
本文的内容主要是 程序的表示、转换与链接 这门课第二周的内容,主要介绍了浮点数和整数在机器内如何编码和存储 (大端和小端) 的,了解这些细节后,能够更好地理解代码中进行数值计算和比较时出现的违反直觉的结果,同时也能避免出现这样的问题。
数据在机器中都是 01 编码的,而在程序中常用的数值类型是整数和浮点数,下面会描述下两者在计算机中的表示方式,且会重点描述浮点数部分
整数的表示
整数主要分为带符号(signed) 和无符号 (unsigned)的,需要注意的是无论是否带符号,整数在内存中都通过补码来表示,正数和 0 的补码就是该数字本身。负数的补码则是将其对应正数按位取反再加 1
对于 C 语言,需要注意的是,若同时带有无符号和带符号整数,C 编译器会将带符号整数强制转为无符号数,比如说对于如下关系表达式,某些结果并不符合直觉就是由这个原因引起的
下图中的后面带 U 的数字表示这是个无符号的整数,反之就是有符号的,其中标红的就是结果不符合直觉的例子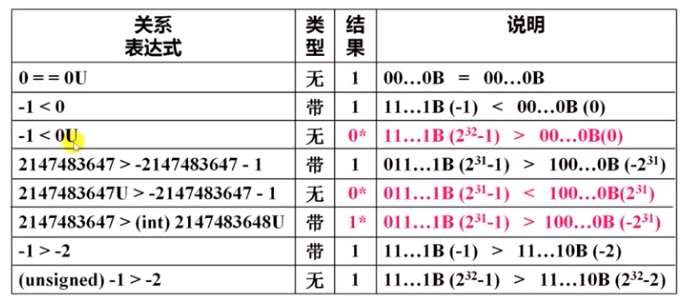
上面那三个不符合直觉的例子原因分析如下
- 第三个例子由于右边的 0U 是个无符号数,因此左边的 -1 也被解析成一个无符号数,而其补码是 32 个 1,被解析成无符号整数后就是 \(2^{32}-1\)
- 第五个例子由于同理,右边的结果 -2147483648 的补码是首位的 1 加上 31 个 0,被解析成无符号数后就是 \(2^{31}\)
- 第六个例子中, 2147483648U 的补码同样也是是首位的 1 加上 31 个 0,但是因为前面加了一个 (int) 后被转换成一个带符号整数,则在解释的时候变成了 \(-2^{31}\)
同理,在 printf 时通过 %u 和 %d 分别将整数解析成无符号和带符号的,因此也会出现如下结果
浮点数表示
在介绍浮点数之前,先介绍一些移码的含义,因为在浮点数的表示中用到了这个概念
整数的通过 01 表示很好理解,那小数中的小数点该如何在计算机中表示?采用的基本思想就是用科学计数法来表示小数,然后将科学计数法中不同部分 (包括正负、尾数部分和指数部分三大部分) 分段存储在 01 序列中,如下是详细的描述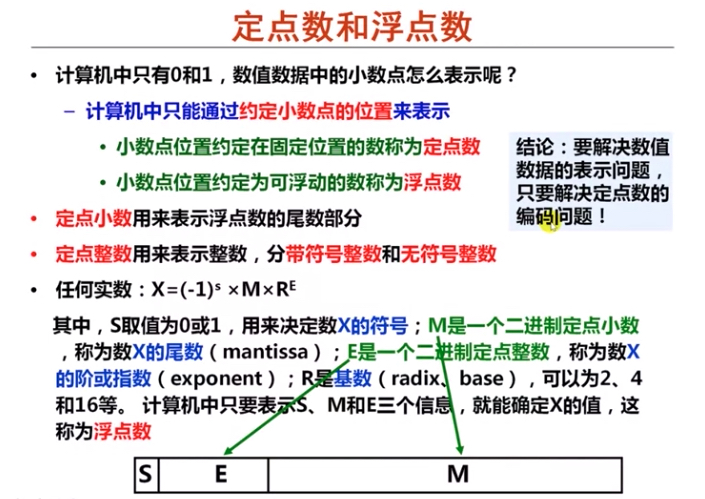
上面提到了任何实数都能通过科学计数法表示成 \(X=(-1)^s × M × R^E\), 而在计算机中都是二进制表示的,因此 R 固定为 2
而 M 的取值则可以有很多种方式了,如让 M 的取值小于 1 且小数点后第一位为 1, 则对于十进制的 12.0,写成二进制是 1100.0,相当于 \(0.11×2^4\),则可以得出 s=0,M=0.11,R=2,E=4; 且由于 M 的小数点后第一位总是 1,可以将其省略掉,则对于浮点数有以下的表示方式
而在通用的 IEEE754 标准下,定点小数 M 是一个值在 1-2 之间的数;比如说对于十进制的 12.0,写成二进制是 1100.0,相当于 \(1.1×2^3\),则可以得出 s=0,M=1.1,R=2,E=3;而对于十进制的 - 12.0,相当于 - 1.1×2^3 吗,则 s=1,M=1.1,R=2,E=3,因此 IEEE745 的标准跟上面的很类似,具体如下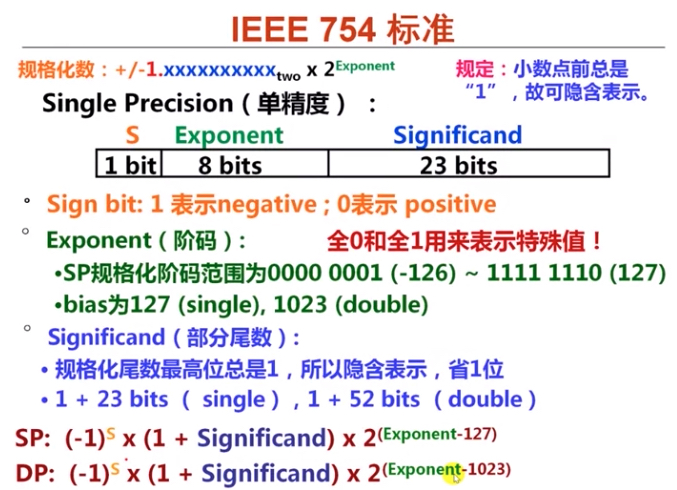
如下是通过 IEEE754 标准来存储和解析浮点数的两个简单的例子
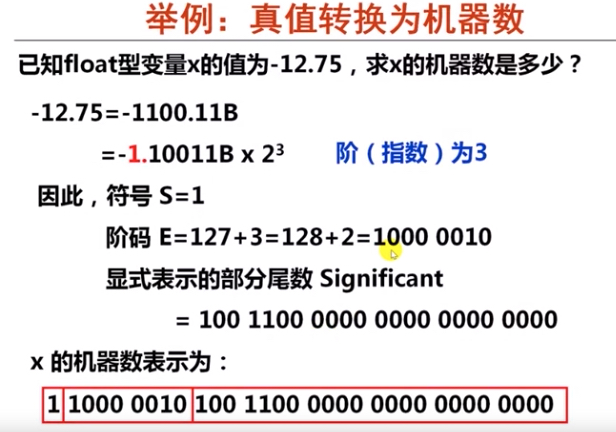
上面的 IEEE754 标准中,阶码是全 0 和全 1 表示的是特殊值,而这可以分为以下几种情况
| - | 尾数 M 全 0 | 尾数 M 非全 0 |
|---|---|---|
| 阶码 E 全 0 | 0 | 非规格化数 / Denorms |
| 阶码 E 全 1 | 无穷大 | 非数 / Nan (Not a number) |
Nan 表示的是不合法的数值如 \(\sqrt{-4.0}\)、\(0/0\)、\(+\infty+(-\infty)\) 等都是非数
而 Denorms 则是被用来标识前面通过 IEEE754 标准中最小正数到 0 之间的这段距离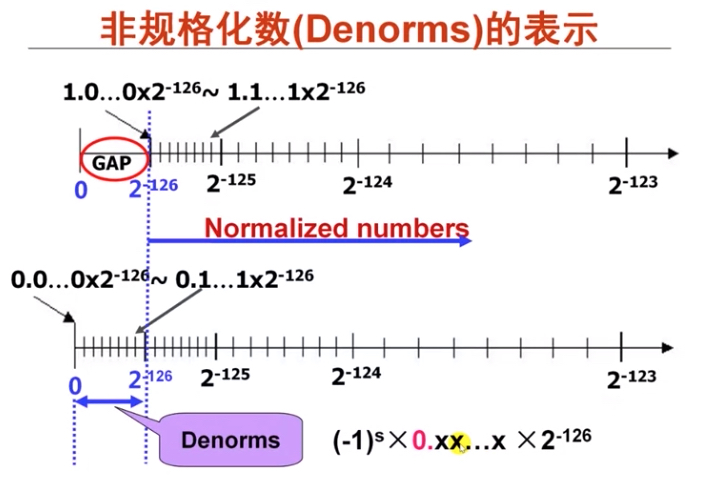
从上面的描述中可知,并非每个浮点数都可以用 01 精确表示,对于那些无法找到精确表示的浮点数,只能进行舍入来进行近似,如下图所示是一个例子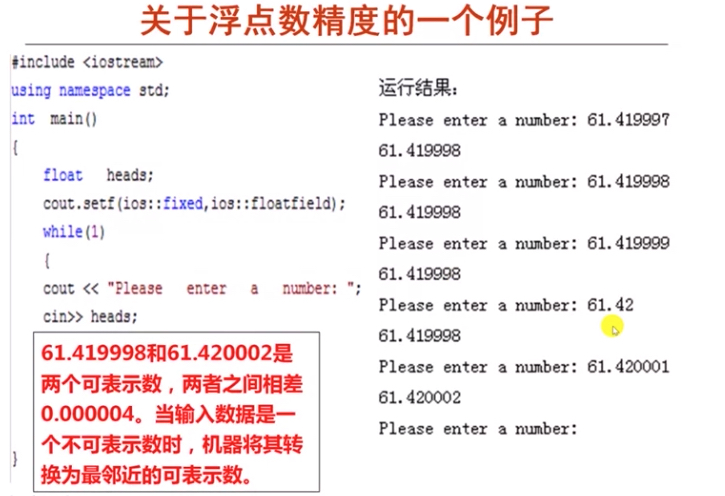
大端与小端
大端与小端其实就是数据的字节在地址中是如何排列的:大端指的是 MSB 所在的地址是数的地址,小端指的是 LSB 所在的地址是数的地址

小结
week2 的内容很多细节,但是比较重点的就是整数和浮点数是如何在计算中表示和存储的,其中整数都是以补码来表示的,同时要注意同一个补码会根据上下文被解析成 signed 或 unsigned,而这会导致一些违反直觉的情况出现;而浮点数通过科学计数法写成了三个主要部分:正负号、尾数和指数,并在计算机中分三段分别存储这些数,解决了无法直接表示小数点的问题,单精度和双精度的表示凡是是一致的,只是各个段的长度不一,需要注意的是,并非每个浮点数(这个集合是无穷大)都可以用 01 精确表示,对于那些无法找到精确表示的浮点数,只能进行舍入来进行近似,因此在浮点数进行比较时要慎重使用 ==