Dynamic Creative Optimization in Online Display Advertising

发表于 2022-02-01 标签计算广告

最近在研究广告创意相关内容，笔者根据当前的调研，将这个领域划分为创意生成、创意优选和创意投放三大块，每一块的具体职责如下

创意生成：利用素材 (标题、图片、视频、落地页等) 生成候选创意 (用户看到的广告)
创意优选：从计划的候选创意 (一个计划下的候选往往有多个) 中选择 topk 个用于投放
创意投放：将优选出来的创意投放至线上

严格来说，这三部分其实也并非泾渭分明，比如前两部分可以统一理解为创意生成 (从最原始的素材生成最终要投放的创意)，后两部分可以统一理解为创意投放过程 (从候选中选出来并投放至线上)。

本文主要侧重讲述与创意投放相关的一篇 paper, 而且偏向于上面提到第三块内容 (没有基于 E&E 的优选过程)，paper 的标题是 Dynamic Creative Optimization in Online Display Advertising，这篇 paper 将素材在线投放问题建模成一个二部图匹配问题，并提供了严格求解的方法和在线的近似求解方法。更重要的是，这种建模的方法不局限于创意领域，能应用到更多投放场景下。

问题建模

online advertising 的绝大多数方法，如 targeting、ranking、bidding 等，本质上都是在解决在线分配问题，即让合适的广告分发给合适用户，从而使得收入最大化（同时需要考虑生态、用户体验等），因此也可以从分配的角度去构造出一个如下简单二部图的形式，左边是 user，右边则是具体的广告 (在这里为创意), 连接的边表示这个用户访问了这个广告 / 创意，边的权重可根据具体的业务目标决定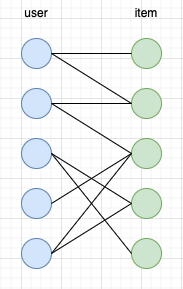

基于上图的二部图，paper 里将问题建模成如下的最优化问题

符号含义如下

$u$: user 的 index
$i$: item 的 index, 这里的 item 指的是创意 (creative)
$r_{iu}$: 第 $u$ 个 user 访问了第 $i$ 个 item 的 revenue，比如消耗 / 点击等，即上图中的边权
$T_u$: 第 $u$ 个 user 的总访问次数
$x_{iu}$: 第 $u$ 个 user 访问了第 $i$ 个 item 的次数
$\underline{k_{iu}}$: 第 $u$ 个 user 访问了第 $i$ 个 item 的次数的下限
$\overline{k_{iu}}$: 第 $u$ 个 user 访问了第 $i$ 个 item 的次数的上限
$y_{iu}$: 第 $u$ 个 user 是否访问了第 $i$ 个 item
$l_i$: 第 $i$ 个 item 触达的不同用户数的下限 (防止只给一个用户出广告)

上面的最优化问题中，(1b) 到 (1d) 中的三个约束，对应的是如下三个约束

(1b) ad fatigue constraint, which aims to help in avoiding customers becoming fatigued by seeing a product too many times. This constraint says that a particular item $i$ can be shown at most $\overline{k_{iu}}$ times to user $u$. To calibrate ad fatigue, this parameter can be set using historical data showing when customers stop engaging with ads.
(1c) ad retargeting constraint, which focuses on showing products to customers that have seen or searched for them before. In this constraint, we say that a particular item $i$ has to be shown at least $\underline{k_{iu}}$ times to user $u$. To retarget an ad, this parameter can be set postive for items that the user saw just before the ad campaign is planned.
(1d) user diversity constraint, which addresses the requirement that advertisers want to increase reach and purchasing by showing their products to many different customers. This constraints says that at least $l_i$ users have to see a particular item $i$. These parameters are specifically set by the advertiser.

问题求解

这里问题的求解分为了离线和在线两部分，区别是离线时是以上帝视角看这个问题，即能够获取用户的访问次数 $T_u$，但是在线时则是不知道的。因此，离线可采用严格的求解方法，在线则只能采用近似的求解方法。

离线求解

假如能够获取 $T_u$（即用户当天的访问次数），就能够采用来求解上面的最优化问题，这类问题通常会被变换成一个网络流问题来求解，关于网络流更详细的介绍可以参考算法学习笔记 (28): 网络流

而上面建模出来的问题，可以被转变成网络流中的最小费用最大流问题 (minimum-cost flow problem), 这部分更详细的描述也可参考算法学习笔记 (31): 最小费用最大流

因此，基于最小费用最大流的概念，可以构造出如下的网络流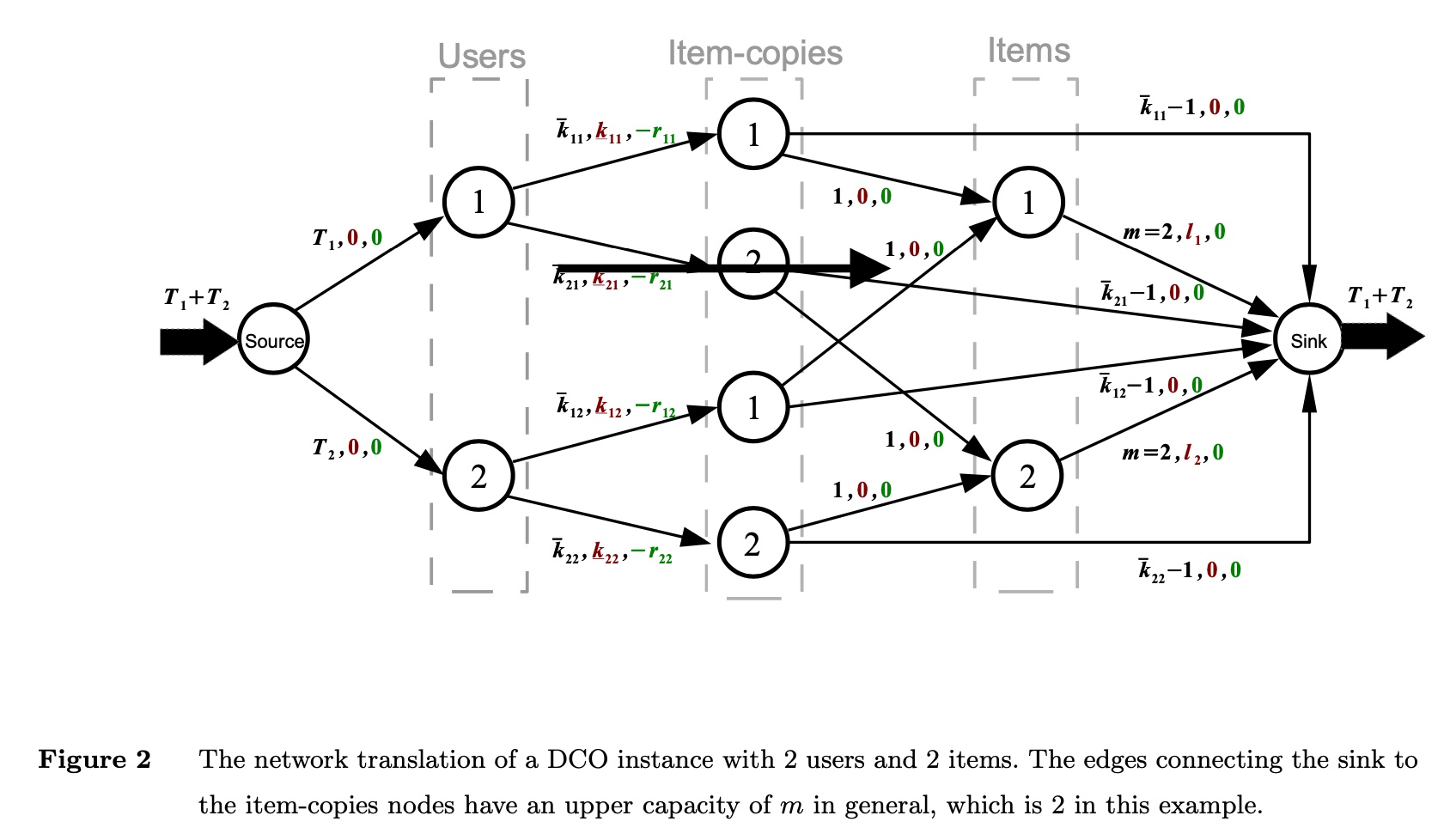

上面的网络流中有 2 个 user 和 2 个 item，理解以下几点就能够理解上图的含义了

每条边的三个参数的含义分别是 (流量上限，流量下限，费用)
从 source 出发到第 $u$ 个 user 的流量上限为 $T_u$(即用户当前访问的次数)
每个 user 访问每个 item 的次数的上限（ad fatigue constraint）和下限（ad retargeting constraint）的约束体现在 users->item-copies 的边上
item-copies->items 的连边是为了满足上面的 user diversity constraint，即保证访问第 $i$ 个 item 的不同用户的数量不小于 $l_i$
item->sink 中，流量上限为 $m$, 即访问第 $i$ 个 item 的不同用户数的上限是总用户数

此外，在构图中还需要考虑如下几个问题，paper 里没有给明确的答案，也算比较 open 的问题，需要针对不同的业务场景设计对应的技术方案了

(1) 边的权值 (即上面说的费用的负值) 的物理含义是什么？缺失的边的权值怎么计算？
(2) 采用 id 粒度过小可能导致整个图可能过大，进而导致图的求解比较困难，如果做 clustering 要怎么做？
(3) 新 uid/item-id 如何处理？

在线求解

上面的解法是离线解法，即能够拿到了用户当天的访问次数 $T_u$, 然后用严格的方法求解最优化问题，这个模式往往可以用来大致摸底方法的收益天花板（通过回放历史精排日志），但是在实际投放中，并不知道用户当天的访问次数 $T_u$(笔者附：如果用历史平均来近似，误差会有多大？)，因此在线需要提供一种近似最优的求解方法

deterministic algorithm

paper 指出了 deterministic algorithm（简单来说就是不会有 random 操作，反例是启发式算法）对于在线问题表现效果很差，至于有多差，paper 给了一些证明，这里略过过程，只给出其中一些核心概念和结论

paper 在这个过程中使用了 competitive ratio来衡量 deterministic 算法的效果，这个指标主要用来描述极端情况下，online algorithm 的效果相比于 offline 的有多差，引用这个讲义里的定义如下

The competitive ratio of an online algorithm for an optimization problem is simply the approximation ratio achieved by the algorithm, that is, the worst-case ratio between the cost of the solution found by the algorithm and the cost of an optimal solution.

有了 competitive ratio 的概念，paper 针对 deterministic algorithm 给出了如下结论（证明的详细过程可以参考 paper 中的 4.1 小节)，即 deterministic algorithm 的效果很差，哪怕给 reward 加了 bound

Proposition 1. The competitive ratio of any deterministic algorithm for the
online DCO problem is arbitrarily small
Proposition 2. Suppose that the revenue associated to all item and user pairs are bounded, that is, there exists an $r$ such that $\underline{r} ≤ r_{iu} ≤ 1$ for all items $i$ and users $u$. In this case, the competitive ratio of any deterministic algorithm for the online DCO problem is $\underline{r}$

deterministic algorithm with assumption

上面给出的结果中，没有任何的假设，因此在这个方法中加入了一个 assumption：即用户 $u$ 每天至少有 $c_u$ 次访问，paper 中引用了 IAB (Interactive Advertising Bureau
) 的一个结论，认为这个数据是比较容易能得到的，paper 描述如下，

Using historical data, advertisers can make accurate estimates about the minimum number of times they expect a user to visit the platform during the advertising period (Interactive Advertising Bureau 2020).

但是 paper 中给出了这一结论的参考资料中似乎只是一些统计数据的罗列，并未提及上面这个结论的推导过程。。。而从逻辑上讲，笔者猜测虽然用户 $u$ 准确的访问次数 $T_u$ 比较难预测，但是这个访问次数的 lower bound $c_u$ 的难度也许会比较容易获得

在 $c_u$ 比较容易获得的 assumption 下，paper 里给出了第一种在线算方法，总体算法流程如下

其实跟 offline 的区别不大，就是用了 $c_u$ 替换了 $T_u$, 在线分配时优先满足约束，而满足了约束后，就可以在 ad fatigue 的约束下去拿 highest revenue 的边

paper 里绕了一大圈才给出了上面的算法流程，给出了各种符号、 lemma、proposition，但是跟最终的结论的关系又不是非常大，有点凑字数的感觉；而且比较核心的部分即 $c_u$ 是如何获取的则是基本没怎么提。。。

paper 里还给出了这个算法的 competitive ratio 的 lower bound 是（证明过程可参考 paper，这里略过）

\[\begin{align} 1-\frac{(\overline{r} - \underline{r})n_1}{\underline{r}(n_1+n_2)} \end{align}\]

各个符号含义如下

$n_1=\sum_{u=1}^{m} c_u$: 即所有用户的最少访问次数之和
$n_2= T- n_1$: $T$ 是所有用户的实际访问次数之和
$\underline{r}=\min_{i=1 \dots n, u=1 \dots m}r_{iu}$: 即所有 pair 的 revenue 的最小值
$\overline{r}=\max_{i=1 \dots n, u=1 \dots m}r_{iu}$: 即所有 pair 的 revenue 的最大值

greedy algorithm

paper 里还提到到了另一种贪心的算法，其 assumption 是每个 item/user 都有一个 reserved revenue, 第 $i$ 个 item 的 reserved revenue 记为 $
_i$, 第 $u$ 个 user 的 reserved revenue 记为 $\beta_u$, 则有

\[\begin{align} r_{iu} = \alpha_i + \beta_u \end{align}\]

基于这个假设，paper 里给了如下的 online algorithm，并且证明了这里的 competitive ratio 能跟最优的一致

但是笔者觉得这里的 assumption 有很大的问题，即假设了每个 item 对所有 user 的 revenue 是一样的，这样显然不合理，因为正是每个 user 的兴趣不同，才需要进行个性化的推荐，也是当前推荐 / 广告里各种算法和策略有效的原因，所以这里的算法笔者觉得可以看一下数学的原理，但是在实际应用并不现实

小结

总的来说，这篇 paper 将在线广告的分配建模成一个经典的二部图问题，提供了离线和在线的解法，并给出了一些理论证明，笔者觉得可以学习一下其中的思想，但是如果照搬 paper 的方法在实际应用的话比较难

第一个 online algorithm 的问题在于 $c_u$ 的获取并没有给出具体的方法，第二个 online algorithm 的问题在于本来的 assumption 就不合理

笔者认为利用用户 $u$ 过去一段时间的访问次数来近似（或者通过预估的方式）作为其未来的访问次数 $T_u$ 是一种可行的方法，但是这个方法还需要解决如下的问题

（1）如果求解出来某个 item 需要分配给某个 user，paper 里说了是直接展示，但是在实际的系统中往往是 “召回 + 精排” 的结构，需要如何保证这个 item 一定能被 user 看到？或者说，实际中的系统往往已经有一套召回和精排的策略，怎么让这套新策略融入现有的系统中

（2）user-item 边的权值的物理含义是什么？缺失的边的权值怎么计算？

（3）采用 id 粒度过小可能导致整个图可能过大，进而导致图的求解比较困难，可以怎么做，如果做 clustering 怎么保证两次聚类的结果差异性不大？

（4）新 uid/item-id 如何处理？