A Hybrid Bandit Model with Visual Priors for Creative Ranking in Display Advertising
之前的文章 Dynamic Creative Optimization in Online Display Advertising 中提到,广告创意往往可分为创意生成、创意优选和创意投放三大块,本文主要讲创意优选这部分的一些做法,这个过程一般会涉及到 E&E 的过程。
本文的主要内容是选自阿里发表的一篇 paper:A Hybrid Bandit Model with Visual Priors for Creative Ranking in Display Advertising,paper 通过 list-wise 的训练方式达到对同一计划下的候选创意进行排序 (即优选) 的目标;list-wise 可以算作 Exploitation 部分,paper 还通过了一个 bandit model 达到 Exploration 的目的,总体的做法比较合理,也在业界实际场景验证了有效性,值得一看。
paper 里提出的方法主要分为两大模块:VAM (visual-aware ranking model) 和 HBM (hybrid bandit model), 总体的模块图如下所示,VAM 即上面提到的基于 list-wise 优选做 exploitation 模块,HBM 则是基于 badnit model 做 exploration 模块,下面也主要从这两个模块进行介绍。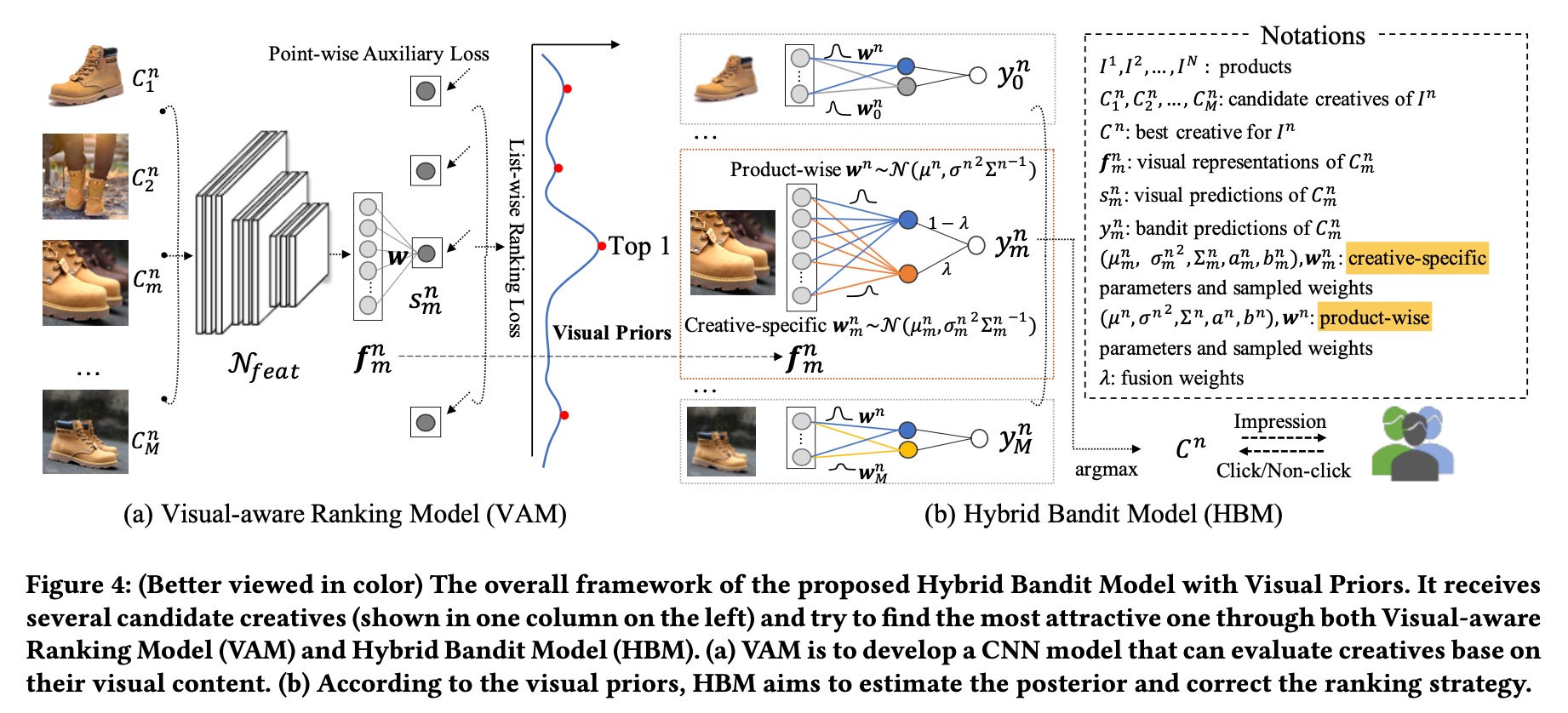
VAM
list-wise loss
list-wise 是 learning to rank 里一种建模方式,另外两种分别是 point-wise 和 pair-wise,常见的 ctr/cvr 预估都是采用 point-wise 的方式;
关于这几种建模方式可参考下面两篇 paper,两篇都是 Microsoft 发表的 paper,第一篇讲了 point-wise -> pair-wise 的过程,第二篇讲了 pair-wise 到 list-wise 的过程
- From RankNet to LambdaRank to LambdaMART: An Overview
- Learning to Rank: From Pairwise Approach to Listwise Approach
VAM 采用的 list-wise loss 即是第二篇 paper 中的提出的 loss,其流程如下图所示,更详细的推导可参考上面第二篇 paper

VAM loss
回到 VAM,上图的 query 相当于商品 (product),而 list 则是每个 product 对应的所有创意 (一个 product 往往会有多个候选的创意)
因此,list 中的每个 item 的 prediction
adjust the scale of the value so that make the probability of top1 sample close to 1,则对于第
除了常规的 list-wise loss, paper 里还添加了一项 point-wise 的 auxiliary regression loss,其含义也比较直观,就是让 VAM 的 prediction 尽可能接近其真实的 CTR 值,其表示如下
根据原文的描述making the outputs close to the real CTRs will significantly stabilize the bandit learning procedure,其作用是让后续的 HBM 训练更加稳定,则第
noise mitigation
这里的 noise mitigation 指的是部分创意的 impression 会比较少,统计的后验 CTR 波动性较大 (极端的比如只曝光一次),
一个粗暴的方法是对 impression 卡个阈值,小于阈值的 item 就不作为训练数据,但这样可能会导致训练的数据量过少,paper 里采用了如下 2 种方法
第一种方法是 label smoothing, 也是这篇 paper 提出的方法 Click-Through Rate Estimation for
Rare Events in Online Advertising,其思想是基于贝叶斯学派给点击数 clicks 和 CTR 值整个先验分布,这样遇到极端值时也有分布约束,导致最终的值不会太离谱,
第二种方法是 weighted sampling,就是给点击数少的样本更小的权重,paper 的做法是对点击数取了个 log 变换作为这个样本的 weight。
HBM
HBM 本质上是一个 Bayesian Linear Regression,从名字大概就能猜测,这个是贝叶斯学派的方法,即认为模型参数是服从一个分布,通过从分布里采样达到 exploration 的目的,其推导过程如下
假设线上的数据按照如下方式产生,
paper 里将
参考上面 wiki 的推导过程,总体模型的 training 和 serving 过程如下所示
公式 18 可以认为是 training 过程 (对于贝叶斯方法,有个特定的名字 Bayesian inference),在贝叶斯的方法中,更新模型就是更新假定的 distribution 中的各个参数,本例中就是上面两个分布中的
而 serving 则是从 training 得到的分布中抽样得到
上面的计算 score 的方法是第
paper 这样做的原因是
This simple linear assumption works well for small datasets, but becomes inferior when dealing with industrial data. For example, bright and vivid colors will be more attractive for women’s top while concise colors are more proper for 3C digital accessories. In addition to this product-wise characteristic, a creative may contain a unique designed attribute that is not expressed by the shared weights. Hence, it is helpful to have weights that have both shared and non-shared components.
所以 paper 根据曝光量算对 score 算了一个权重
则最终的 socre 如下
这里的思想是在某个 product 的曝光量充足时,更加相信其 product-wise 的 score,反之则更相信 creative-wise 的 socre
但是笔者对这里的做法存疑,笔者认为这个
因为如果每个 creative 都有足够的后验数据来进行训练,那做到 creative 粒度的个性化参数效果上应该会是最好的,但是问题是现实是很多 creative 的后验数据非常系数甚至是没有后验数据的,这个时候采用 product-wise 的 score 相当于是做了一个 clustering,笔者认为这样更加 make sense
因此,HBM 的算法流程如下图所示

实验
paper 里采用了 2 个评估指标:Simulated CTR (sCTR) 和 Cumulative regret, 前者模拟 online learning 过程,后者则是评估 bandit model ,两者计算方法如下,但是好像这两个指标不是非常通用?


采用的评估数据集有 2 个,一个是自建的,另一个是公开数据集,效果上自然也是 paper 提出的效果最好,但是 paper 没有做在线的 ab 实验,逼近离线指标跟线上的效果还是有 diff 的
小结
总的来说,这篇 paper 提出一种 creative selection 的方法,由 VAM + HBM 组成,笔者认为有以下几点值得学习
- VAM 利用投后数据 (ctr), 通过 list-wise 方法学习出 creative 的 visual representation
- HBM 利用 VAM 的 visual representation 通过 bandit model,来实现 exploration 部分,同时考虑了 product-wise 和 creative-wise 建模和预估 score 的融合
但是也有以下几点笔者是存疑的
- product-wise 和 creative-wise 的分数时,
参数只考虑到 product-wise 的信息,没能很好体现 creative-wise 的权重,具体原因上面说了 - 广告系统通常是召回 + 精排的环节,精排往往是 creative 粒度的,上面提出的系统未必能完整地融入现有的广告系统,倒是 VAM 训练得到的 visual representation 作为精排模型的一个 feature 是一种可能的方法
- VAM 已经可以对候选创意做优选了,为什么还需要 HBM 来做 exploration?或者说 exploration 是为了拿什么收益? 根据笔者的经验,在广告系统中 exploration 意味着破坏原来系统 feedback loop 所形成的分布,这往往会破坏系统由于马太效应形成的稳态,往往会造成收入的下降,相对应兑换的是一些生态指标或者信仰指标的提升。