浅谈算力优化
当前的推荐或广告系统基本都是做到请求级别的预估和优化,在效果最大化的同时带来的问题是机器成本的上升;而流量分布的不均匀使得这个问题更为严峻,比如说对于抖音或美团,一天内流量往往有两个峰:午高峰和晚高峰,因为这两个时间点餐、刷手机的人数会陡增,而其他时间段流量会下降比较多,如下图所示
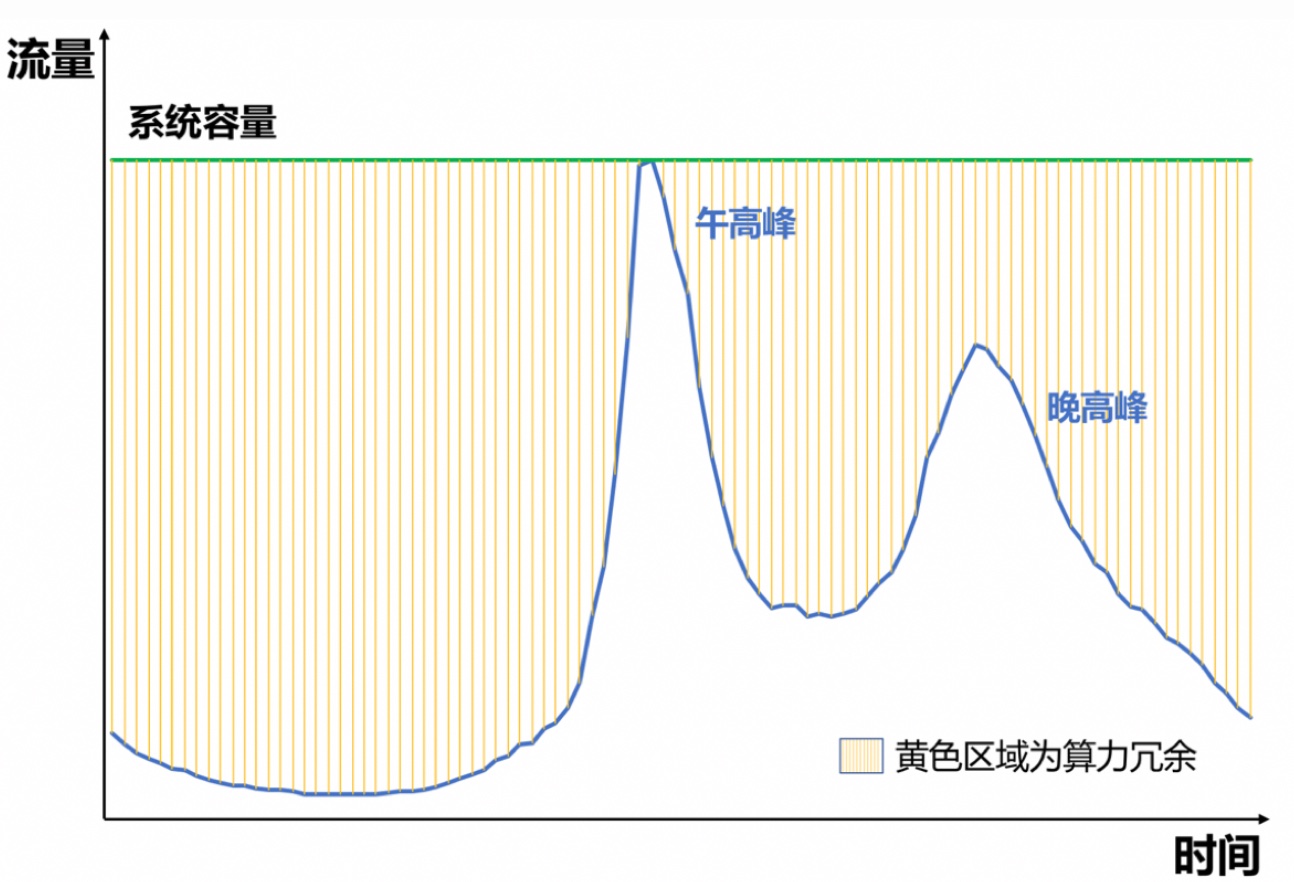
这意味着如果准备足以抗住高峰的机器,那在其他时间段大部分机器是空转的,或者说 roi 很低,因此往往在高峰的时候都需要扩容或降级。降级一般是指指降低请求数,按比例 drop 流量,但是 drop 流量对总体效果肯定是有损的,因此也衍生出了算力优化这个研究方向,算力优化本质上就是做效果和机器成本的 trade-off, 或者说如何尽可能无损地降本
本文主要介绍一些算力优化的常见手段,笔者将其总结为 drop、cache 和 dynamic 三类方法;而如果把消耗的算力拆解,可以直观拆成 2 部分:请求量 × 请求消耗的算力,因此可以从这两部分出发去优化算力
- drop:直接把流量 drop 掉,即直接减少 “请求量”
- cache:将之前的预估结果存到缓存中,每次预估不用经过实际机器的 inference,即减少了 “请求消耗的算力”
- dynamic 则是根据请求的价值,动态控制每条请求消耗的算力,这个方法也是减少了 “请求消耗的算力”,DCAF 是这类方法的代表
上面的几个方法都是偏流量维度的优化,还有一些方法是对模型 inference 的 耗时进行优化的,主要方向是计算并行(硬件升级)、模型压缩(量化、蒸馏、结构调整等),本文就不详细展开了
drop
drop 流量可以说是最原始和粗暴的降级手段,但是在流量突增等场景还是比较有效和立竿见影的手段,除了无差别地 drop 流量的粗暴方式,还可以进一步做得更精细:通过 rule-based 或 model-based 手段来判断一条流量是否要 drop
rule-based 的方法往往需要定义具体业务中的无效请求,比如说这里的 “无效” 在推荐可能是一些用户无点击且停留时长短的请求,在广告可能是由于没有曝光导致的无扣费等。这样的话就可以梳理出一些基本的规则,比如说针对连续 n 次出无效请求的用户,在下一次的请求可以直接 drop 掉
model-based 的方法跟 ruled-based 方法差不多,一般可建模成一个分类或回归的问题;如果是分类问题,需要明确定义二分类中的正例和负例 (即无效请求);如果是回归问题,需要定义每条流量的价值(如推荐或广告最终排序时使用的预估分)
这里值得注意的点是 为了数据集无偏或者说避免 feedback loop, 需要从不生效 drop 策略的流量中随机划一部分来生成训练集(holdout 数据集)
cache
cache 也是常用的一种节省算力的手段,即把之前请求的预估结果缓存下来,然后相似请求过来后,把缓存的预估结果直接返回;这里有 2 个关键问题
(1) 缓存的粒度,一般粒度越细,预估结果越准确,但同时消耗的 kv 存储会越大;常见的可以考虑的维度包括用户、设备、媒体位置、访问时段等,具体缓存的粒度可以从中选出若干个维度叉乘出来
(2) 缓存的预估偏差,由于不是实时预估的,所以预估偏差往往会比实时预估的要高很多,最直观的解决思路就是在 cache 结果直接再套一个 calibration module(如 Platt scaling);这个问题其实也跟缓存的 TTL 比较相关,一般 TTL 越大,预估偏差会越大,同时消耗资源会越少,所以保证缓存的预估偏差小对节省资源也是有较大意义的,因为这个时候的 TTL 可以设得更长
这里的预估偏差反映在后验上一般是高估,其实是因为被低估了的流量竞价会失败而没法曝光。这个现象跟很多 ab 实验的 “小流量高估问题” 的原因是一样的,实际上并不只是高估,而是预估不准,只是看到的投后数据都是高估投出来的
但这里两者预估不准的原因并不完全一致,前者更多是因为不实时带来的,后者(即小流量高估)本质上则是因为有 2 个模型同时产生训练数据集,两个数据集的分布不太一致(feedback loop),可理解为有 2 个 domain,然后处于小流量 domain 的模型使用了大流量 domain 的模型产生的数据集,总体被大流量的模型的数据主导看不到自身的高估(证据之一就是,如果把两个模型的数据严格隔离开,这个问题会大大缓解,但对大盘有损,因为小流量模型数据太少,这部分流量的变现效率就很低);所以实际中往往会把一些能区分 domain 的特征(如 model name、rit 等)加入到模型里,也能缓解所谓的小流量高估问题
dynamic
dynamic 可以说是研究得最多的方法,其思想也比较符合直觉:根据每条流量预估的价值,动态调整每条请求消耗的算力,如果价值越高,分配的算力越高,反之亦然
基于这个思路,很自然能想到有 3 个需要解决的问题:(1)流量价值的预估(2)算力的预估(3)分配策略
针对第(1)个问题,在搜广推的业务场景中,会涉及到排序的过程,因此可以把排序分数近似作为流量的价值;对于推荐,这个价值的物理含义可能不是那么强,但对于广告这类业务场景,基于 ecpm 的排序就是意味着这条流量能给平台带来的实际收入
针对第(2)个问题,在召回、粗排、精排的经典三段漏斗中,可以把进入各个模块的候选数来衡量算力;值得注意的是:候选数和算力两者是正相关,但不是线性的,后面会详细展开这个问题
针对第(3)个问题,对流量价值和算力进行量化后,可以很自然地用最优化的思路建模这个分配问题,最常见的模式是在算力约束下,最大化流量价值,变量则是每条流量的候选数
分配策略的一个代表性工作是阿里在 2020 发表的 paper,DCAF: A Dynamic Computation Allocation Framework for Online Serving System,paper 主要解决的是上面的第三个问题,下面会先讲 paper 中的分配策略,然后再探讨下流量价值和算力建模的一些思路
DCAF
问题建模
paper 很自然把算力分配建模成如下的问题

上面相关符号含义如下
- \(i\): 请求的 index
- \(j\): action 的 index,这里的 action 一般是指进入各个模块的候选数
- \(x_{ij}\): 是否采用第 i 条请求中的第 j 个 action,取值为 0 或 1,每条请求只能采用一个 action
- \(q_j\): 第 j 个 action 消耗的算力资源,注意这里的假设是相同 action 消耗的算力资源与请求无关
- \(Q_{ij}\): 第 i 个请求中的第 j 个 action 带来的价值
- \(C\): 总体的算力限制
在建模完这个问题后,paper 提到了这种建模方式面临的 2 个重要问题,其实也是这类最优化范式通常都有的问题
第一个是需要实时求解最优化问题,这个问题的原因在于我们通过这种方式建模时,默认是能拿到全部数据的,如果统计过去 n 天的数据是可以做到的,但是在线上实时 serving 是无法做到这点的
这个问题其实跟 bidding 场景下的最优化建模的问题一致,《Bid Optimization by Multivariable Control in Display Advertising》阅读笔记 是一个例子,而 bidding 的一般套路是先通过求解最优化问题求解出最优的出价公式的形式,然后线上通过实时调控的来决定公式里的未知变量,后面我们讨论这个问题的求解时,会发现这篇 paper 里的解决的思路有些不一样,需要直接求解最终的解
第二个是流量价值即 \(Q_{ij}\) 计算的问题,paper 里给出的思路是通过模型预估,且提出了模型需要足够轻量级,因为流量维度的预估 qps 会比较大
问题求解
问题求解是通过拉格朗日对偶方法进行求解的,关于这个方法的原理可以参考这篇文章 凸优化总结 里面的拉格朗日对偶部分, 根据理论可以写出上面的最优化问题的拉格朗日对偶问题如图下式子(3)所示

与 bidding 中的推导不同,在 bidding 中只需要获取最优出价公式而不需要具体的解,因此可以最变量直接求导数为 0 推导出最优出价的公式,这部分详细过程可以参考《Bid Optimization by Multivariable Control in Display Advertising》阅读笔记 中的另一种推导方法
而在这里需要作出具体的决策或者说需要具体的解,即在请求 i 中应该选择哪个 action,即需要让哪个 \(x_{ij}\) 的值为 1,所以需要求解这个问题,paper 的推导过程如下

下面是笔者对上面推导步骤的理解
1)只有当 \(-Q_{ij} + \lambda q_j + \mu_i \ge 0\) 时,公式(3)中的式子才有下界(笔者不太理解这一点,因为这里的 \(x_{ij}\) 取值是 0 或 1,而不是任意整数,所以即使 \(-Q_{ij} + \lambda q_j + \mu_i \lt 0\),也不会出现无下界 (负无穷) 的情况)
2)有了 \(-Q_{ij} + \lambda q_j + \mu_i \ge 0\) 条件后,可以将 min 的约束取消掉,上图的公式 (4)因为这个时候的取 min 一定会使得 \(x_{ij}(-Q_{ij} + \lambda q_j + \mu_i)\) 这一项为 0,这个其实跟推导拉格朗日对偶的过程有点像,如下图所示(来源)

3)取消掉 min 约束后,剩下的 max 问题的变量就是 \(\lambda\) 和 \(\mu\), 从约束条件 \(-Q_{ij} + \lambda q_j + \mu_i \ge 0\) 可以推出 \(\mu_i \ge Q_{ij} - \lambda q_j\),即遍历第 i 个请求下的所有 action 的 \(Q_{ij} - \lambda q_j\) 的最大值,也应该比 \(\mu_i\) 小,又因为 max 问题跟 \(\mu_i\) 是负相关的,所以 \(\mu_i\) 的取值应该为公式(5)所示
4)因此,对于第 \(i\) 个请求,真正生效的约束条件是 \(\max_j (Q_{ij} - \lambda q_j)\), (这个约束条件是紧致的),只有这个时候 \(x_{ij}\) 的值才不是 0, 亦即最终的 action(见公式(6) )
因此,从公式 (6)可知,线上 serving 时,还需要知道 \(\lambda\) 的值(\(Q_{ij}\) 和 \(q_j\) 的建模方法下面一部分会讲)
但是 \(\lambda\) 的解析解在这个问题中比较难求解,paper 在这里做了 2 个假设
假设一:\(Q_{ij}\) 随着 \(j\) 的增加而单调递增
假设二:\(Q_{ij}/q_j\) 随着 \(j\) 的增加而单调递增
假设一的含义是随着候选数越多,能从这次价值得到的流量越大(笔者觉得这里还要加个约束,就是线上的资源能抗住的情况下,否则候选数越多可能会导致错误率增加,流量价值下降,paper 后面提到的一个 MaxPower 的概念就是在讲这个事情),假设二的含义是随着候选数的增加,边际收益是递减的,这个比较 make sense
基于这两个假设,可以推导出总体的算力 \(\sum_{ij} x_{ij}q_j\) 会随着 \(\lambda\) 增大而单调递减 , 这部分可参考 paper 中的 4.2 部分,笔者这里做一个更直观的解释,由上面推导的公式(5)可知,\(\max_j (Q_{ij} - \lambda q_j) \ge 0\), 即 \(Q_{ij}/q_j \ge \lambda\), 而 \(Q_{ij}/q_j\) 的物理意义可以理解为单位算力的收益,由假设 2 可知,随着算力的增加或者说候选数的增加,算力的边际成本是下降的。因此,随着 \(\lambda\) 的增加,意味着对算力成本的要求增加,即候选数需要减少(这其实也是 \(\lambda\) 的一个物理含义)
有了上面的 “总体的算力 \(\sum_{ij} x_{ij}q_j\) 会随着 \(\lambda\) 增大而单调递减” 的结论后,可以通过二分法寻找一个 \(\lambda\) 使得消耗的算力刚好接近总体的算力 quota \(C\),算法如下图所示,11 行的符号应该是写反了

系统设计
DCAF 的总体框架如下图所示,左边部分主要是建模 \(Q_{ij}\), 右边部分则是在线 serving 系统
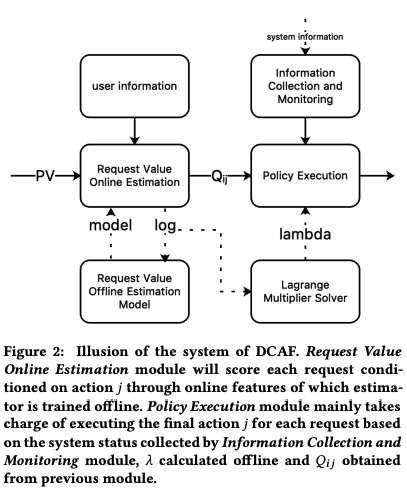
左半部分比较好理解,这里着重讲下右半部分,其中右上角的 Information Collection and Monitoring 部分,会实时搜集当前系统负载的各项数据,如错误率,超时率等,并通过 PID 算法控制错误率和超时率,或者说控制系统当前能承载的上限避免整个系统被打崩,paper 里也把这个称为 MaxPower,可理解为根据系统的实时负载调整每次请求的候选数的上限
这部分在实验设置里也能体现出来,即随着系统负载 qps 增加,MaxPower 会自动下调,保证整体系统的稳定性,如下图所示
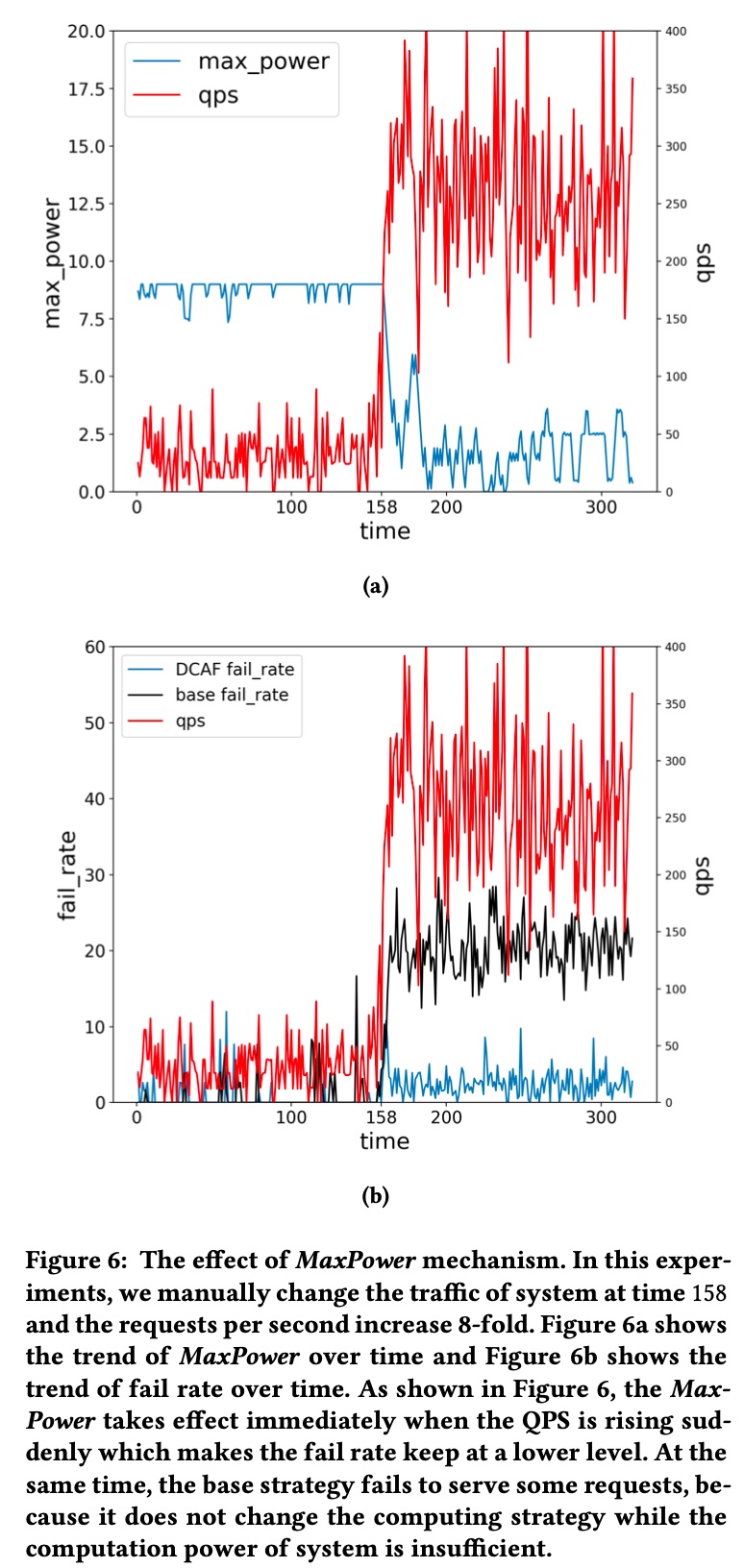
\(\lambda\) 则是根据上面的二分搜索算法,利用采样一段时间的数据实时计算 \(\lambda\) 的最优值,算法中的容量 \(C\) 则是根据 QPS 做了兑换计算,如下是离线计算 \(\lambda\) 的过程

实验设计
实验部分做了 2 个实验,离线和在线的
离线实验主要是做了流量回放,\(\lambda\) 还是按照上面的方法计算,算力 \(q_j\) 表示请求的候选数量, \(Q_{ij}\) 表示算力 \(q_j\) 下候选里 top-k 个 ecpm 广告的和
- Action \(j\) controls the number of advertisements that need to be evaluated by online CTR model in Ranking stage.
- \(q_j\) represents the advertisement’s quota for requesting the online CTR model
- \(Q_{ij}\) is the sum of top-k ad’s eCPM for request \(i\) conditioned on action \(j\) in Ranking stage which is equivalent to online performance closely. And \(Q_{ij}\) is estimated in the experiment.
离线实验结果如下,左纵轴的 ecpm 是实际的流量价值,右纵轴是实际消耗的算力,从结果可知,离线回放能做到算力下降同时流量价值上涨,且随着 \(\lambda\) 值的增大,DCFA 总体消耗的算力和流量价值都是下降的,这个其实跟前面推导 \(\lambda\) 的过程是一致的,因为 \(\lambda\) 的物理含义就是增加候选数的边际收益的一个门槛,随着候选数增加,边际收益是递减的,而小于 \(\lambda\) 时就是要截断的候选数,也就是 \(q_j\) 具体的值
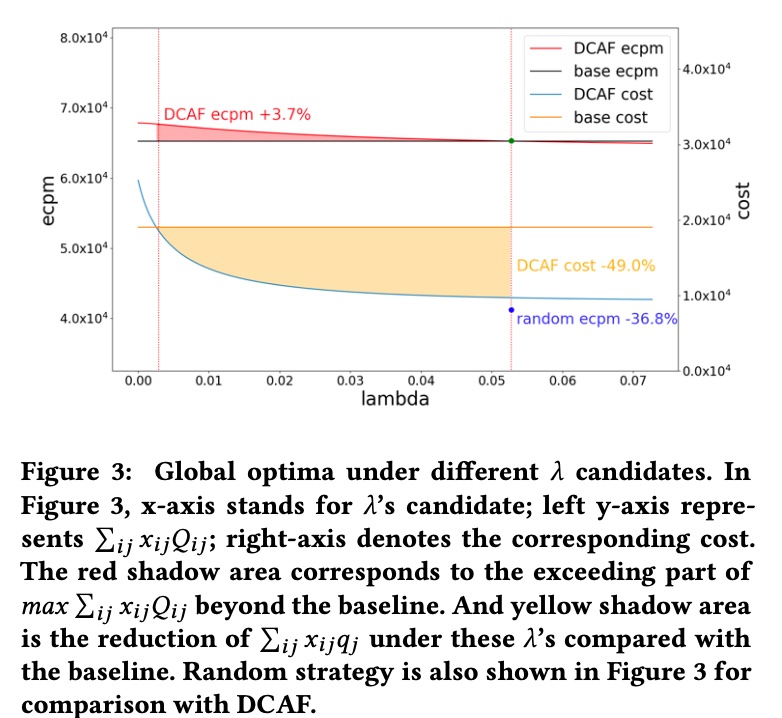
虽然离线实验显示打平算力 ecpm+3.7%, 打平 ecpm 机器成本 - 49%,但毕竟是离线环境,比较稳定,选择的 action 也不会影响环境,所以如果开线上实验,效果一般会打个折扣,paper 里的在线实验也显示了这一点
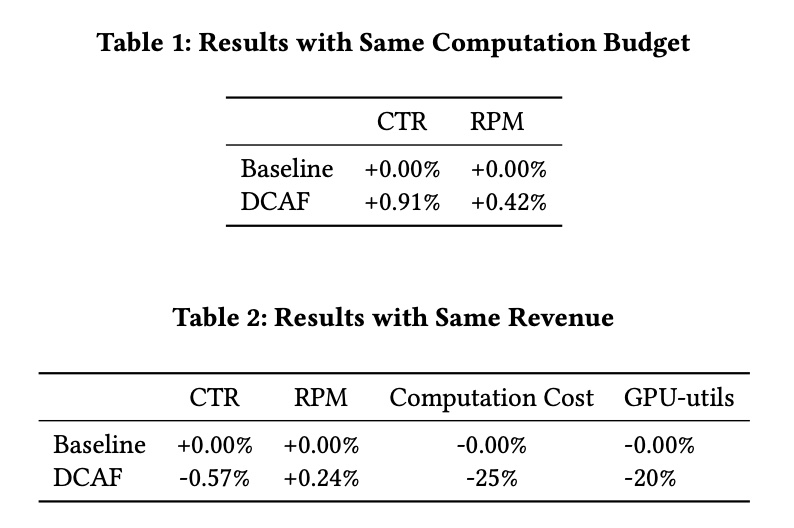
流量价值与算力建模
DCAF 这篇 paper 着重讲了分配策略,但是对流量价值和算力的建模讲得比较少,只提到了 \(Q_{ij}\) 是通过一个简单的线性模型来预估,而 \(q_j\) 则只是候选数,没有进行建模;但是这两个变量的建模对结果影响又是非常大的,尤其是 \(Q_{ij}\)
值得注意的一个点是,流量价值 \(Q_{ij}\) 和消耗算力 \(q_j\) 都跟候选数正相关,且候选越多,越能接近流量的最大价值(错误率可控前提下),同时消耗的算力也会越大
直接把候选数当做消耗的算力不是非常精确的做法,比如说所有候选都只需要抽一次特征,这个时间不会随着候选数增加而增加;而如果以候选数为横轴,算力为纵轴,大概率会画出一条 \(\log(ax)+b\) 形式的曲线(\(a\) 和 \(b\) 是两个参数),即随着候选数增加,边际的算力成本是下降的,\(Q_{ij}\) 同理,所以可以把 \(Q_{ij}\) 和 \(q_j\) 都写成 \(f (候选数)\) 的函数形式
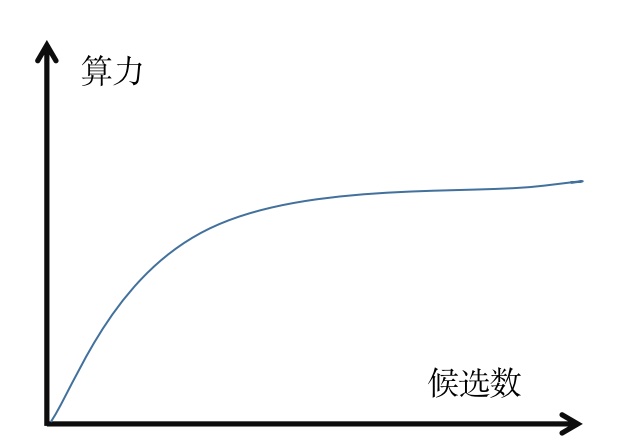
美团在这篇文章中也描述了其对 DCAF 的一个改进,美团外卖广告智能算力的探索与实践,其中就包括了对这两部分的详细的建模,下面会大概讲一下美团的做法,并讨论一下其他可能的做法
流量价值建模
如果直接建模 \(Q_{ij}\)(比如说通过 multi-head 的方式,每个 head 代表一个 action),需要保证 \(Q_{ij}\) 随着 \(j\) 是单调递增的,可以通过在 loss 增加一项 regularization 项来尽量保证预估值是递增的,如在 loss 中增加一项 \(ReLU(pred_{j}-pred_{j+1})\) 来让预估值尽量保序,但这也不能完全保证预估是有序的
针对这个问题,上面的美团的文章的做法是预估整条流量的价值,然后通过每个广告的预估分来估算不同档位的价值(即下图的档位价值预估),这样理论上能够计算所有可能的 action,相比于 multi-head 的做法要更加灵活和轻量级
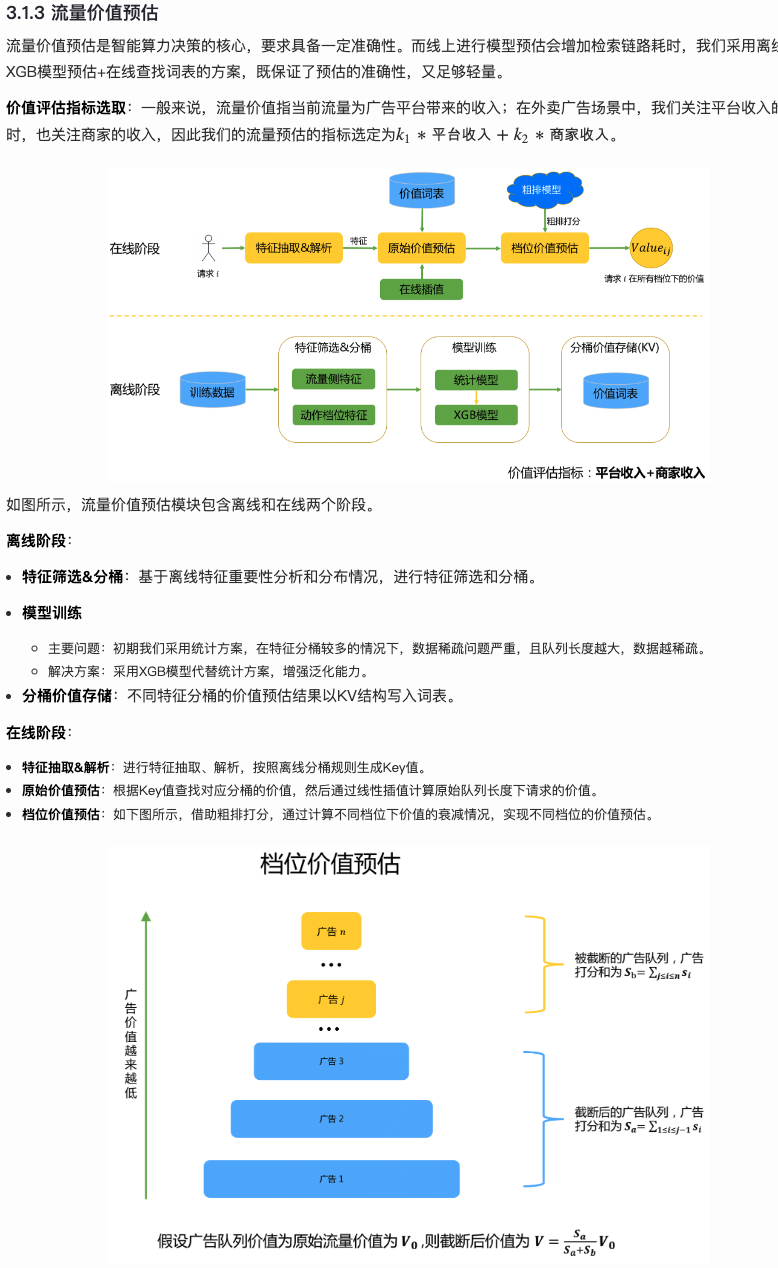
而价值预估上,为了保证在线的效率,美团采用的是 “离线预估,在线查询” 的方法,即离线通过对特征分桶来划分流量,然后通过 xgb 预估每个桶里的流量价值并写入外部 kv;在线时通过实时查询 kv 和插值的方法来 serving,保证任何流量都有一个预估值,最后通过档位价值预估的方法来得到不同 \(j\) 下的 \(Q_{ij}\)
除了这个思路,前面提到了如果以候选数为横轴,算力为纵轴,大概率会画出一条 \(\log(ax)+b\) 形式的曲线(\(a\) 和 \(b\) 是两个参数),我们可以基于这个先验来做更简单的推理和求解,比如说最简单就是基于后验数据直接拟合出 \(a\) 和 \(b\) 这两个参数,但是需要考虑做在何种维度,比如说 user 维度、user × 广告位维度等,核心问题是要考虑做在何种维度,如果维度太细数据过于系数,可能需要考虑做到更大的维度;同时也可以考虑贝叶斯这一类方法
算力建模
美团的文章里算力的建模跟价值的建模很类似,都是离线预估、在线查询的
离线先做特征分桶,然后在桶里建模条数和算力的关系,每个桶的建模采用了分段线性拟合,与上面的价值建模不同的点在于,这里没有插值的过程(就是默认所有流量都能找到对饮的桶?)
而相比于 DCAF 原文采用条数来衡量算力,这里采用了 CPU 的耗时来衡量算力,总体方法如下
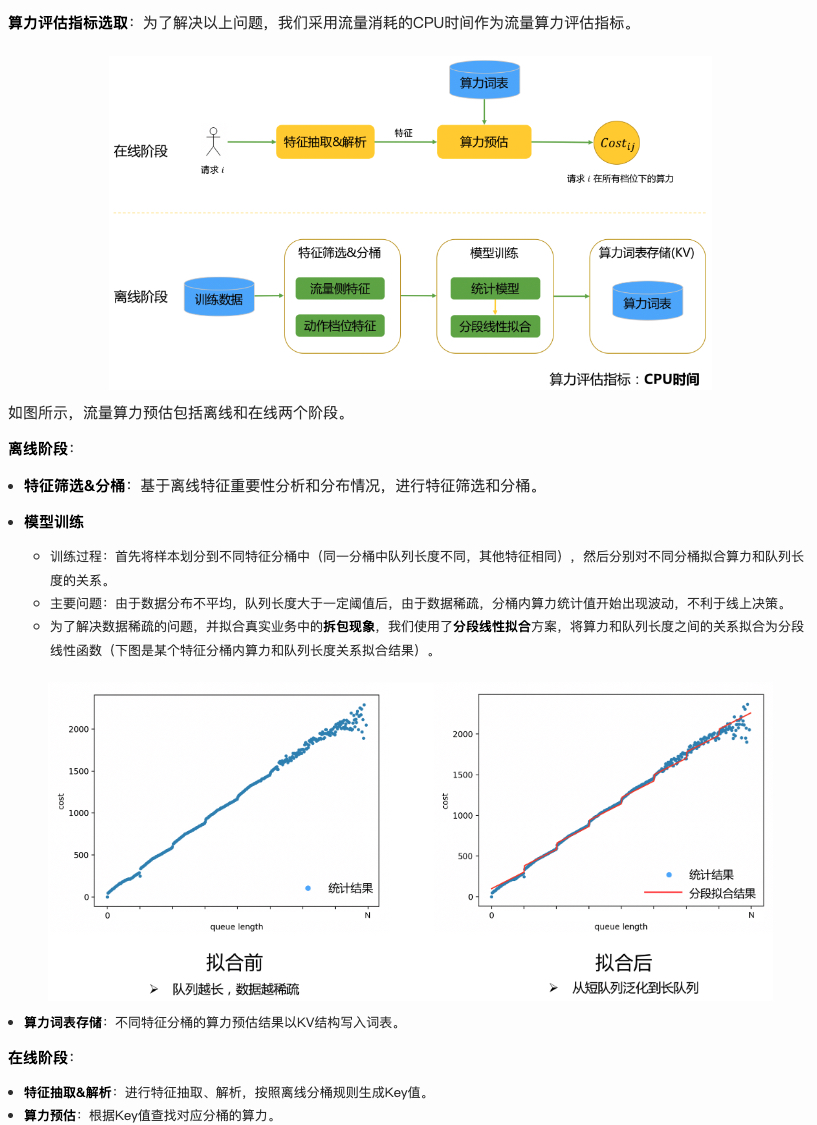
而另一种思路跟上面提到的利用 \(\log(ax)+b\) 形式作为先验比较相似,也是需要考虑在特定维度去拟合 a, b 这两个参数
小结
本文主要从流量维度介绍了一些算力优化的手段,可以将其分为 drop、cache 和 dynamic 三类方法,如果我们把算力拆解为 “QPS× 平均请求消耗算力”,drop 相当于是有丢弃一些低质请求,cache 则是通过缓存降低平均请求消耗的算力,两个方法都比较直观
dynamic 也是在尝试在降低平均请求消耗的算力,或者更准确的说是重新分配算力,做到在打平业务效果减低机器资源,或者打平机器资源提升业务效果;DCAF 是这类方法的一个典型工作,DCAF 对问题的建模和求解比较值得学习,但是对流量价值和算力的建模讲得比较粗糙,美团技术团队的一篇文章对这部分做了较好的补充,本文也提出了建模这两个变量的一个思路;总体来说,这个方法在理论推导和业界落地上都证明了其有效性,值得学习。