回归任务里的损失函数

在搜广推相关业务中，除了 ctr、cvr 这类常规的二分类任务，还存在着预估 stay_duration、LTV、ECPM、GMV 等一系列回归任务

ctr、cvr 这类二分类任务常用的损失函数是交叉熵损失，基本假设是事件服从伯努利分布，最终学习的输出是正样本的比例，而回归任务中存在着非常多种的损失函数可选，如 mse、mae、huber loss、log-normal、weighted logistics regression、softmax 等

每种损失函数都有其假设和适用范围，如果真实 label 分布与假设差异较大，容易导致结果不佳，因此，本文会重点关注这些常见 loss 的推导过程以及假设

MSE/MAE/Huber

这三个 loss 是回归任务中最直观也是最常见的 loss，前两者都假设了误差服从某种特定分布，然后通过 MLE 最终的 loss 形式，huber 则是前两种 loss 的混合版本

MSE 其假设是预估值和真实值的误差服从标准高斯分布，然后写出误差的似然 (likelihood) 函数，并通过 MLE 推导出来最终的 loss 的形式，其推导过程如下图所示（来自 CS229 的教材）

根据误差服从均值为 0 的高斯分布可以写出如下的似然函数

然后根据 IID 的假设和 MLE，可以写出最终的损失函数

MAE 的推导跟 MSE 很类似，只是假设误差服从拉普拉斯分布，把拉普拉斯的概率密度函数替换成上面推导过程中的高斯分布，便能得到了最终 MAE 的损失函数形式

从 loss 函数形式，可以直观看到，对于第 \(i\) 个样本

• MSE 反向传播的梯度大小为 \(-(y^{(i)} - \theta^{T}x^{(i)})x^{(i)}\)
  
• MAE 反向传播的梯度为 \(- \frac{y^{(i)} - \theta^{T}x^{(i)}}{|y^{(i)} - \theta^{T}x^{(i)}|}x^{(i)}\) (其实就是 ±\(x^{(i)}\), 绝对值的求导可参考 绝对值的导数)

从回传的梯度可知，MSE 容易收到异常值的影响，比如说有个异常样本的 label 非常大，则算梯度时 \(y^{(i)} - \theta^{T}x^{(i)}\) 的值也会非常大，容易把样本带偏，而 MAE 受到这一点影响会更小

所以 Huber Loss 也是考虑到了这点，对于 label 较小的样本采用 MSE，label 比较大的样本，则采用 MAE, 整个损失的形式如下图所示

ZILN(Log-normal)

这是 google 一篇预估 LTV 的 paper 中提出来的 loss，A Deep Probabilistic Model for Customer Lifetime Value Prediction

现实任务的数据往往是长尾切稀疏的，拿 paper 里的 LTV 任务为例，会有非常多的 0 值，也存在极端高的值，如下图所示是 paper 里展示的 LTV 的分布（这里的 LTV 含义是首次购买后产生的价值，0 值代表很多客户只购买了一次）

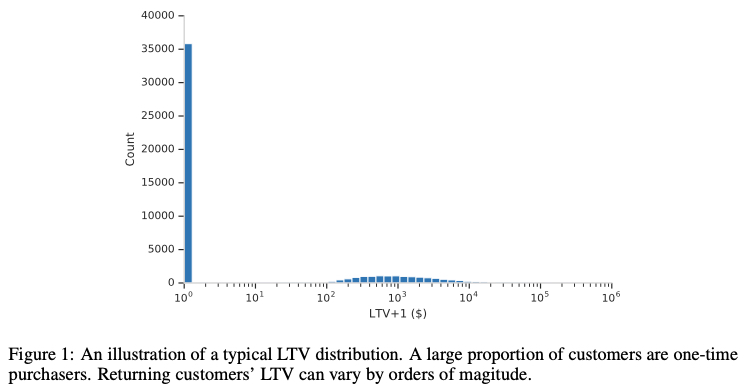
paper 提到直接用 MSE 会有如下问题，其实也是上面提到了 MSE 存在的问题

MSE loss does not accommodate the significant fraction of zero value LTV from one-time purchasers and can be sensitive to extremely large LTV’s from top spenders

所以 paper 提出了 ZILN (Zero-Inflated LogNormal) 的这个 loss，loss 形式如下图所示（注意这里的 \(x\) 是 label)

\[\begin{align} L_{ZILN}(x;p,\mu,\sigma)= -\mathbf{1}_{x=0} \log(1-p) - \mathbf{1}_{x>0}(\log p - L_{Lognormal}(x;\mu,\sigma)) \end{align}\]

这里的 loss 其实有 2 项，对应着 paper 里建模 LTV 分成了 2 个任务，一个是预估购买概率（上面公式里的 \(p\)），另一个是预估购买金额， ，第一个任务是常规的分类的 cross entropy 损失；这种思想其实也比较常见，即引入中间信号建模，这样往往能让总体的效果更好，比如说把 ctr、cvr 分开建模，把 send2click 拆成 send2show 和 show2click 各自建模等

这里重点讲第二个任务，即预估金额的损失 \(L_{Lognormal}(x;\mu,\sigma)\)， 这个 loss 的形式如下图所示，其实就是对 log-normal 分布的概率密度函数取了 log 变换得到的，其隐含的假设是 LTV 服从 log-normal 分布，同时将 \(\mu\) 和 \(\sigma\) 参数化，即用一个 DNN 来预估（注意这里的 \(x\) 仍然是 label)

\[\begin{align} L_{Lognormal}(x;\mu,\sigma)=\log (x \sigma \sqrt{2\pi})+\frac{(\log x - \mu)^2}{2 \sigma^2} \end{align}\]

最终的模型会输出 3 个预估值 \(p\), \(\mu\) 和 \(\sigma\)，如下图所示

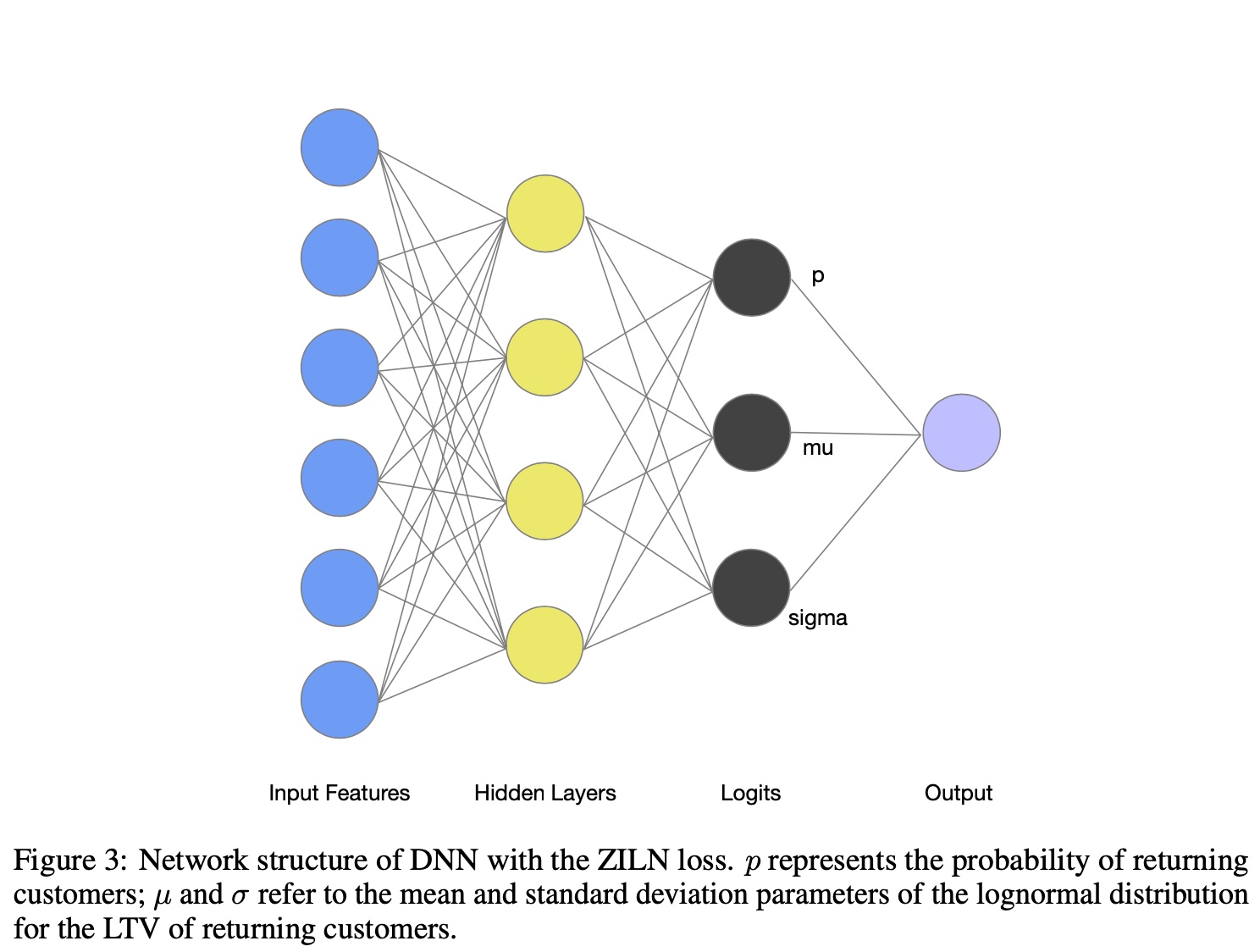
log-normal 形式的推导可以参考前面的 wiki 链接或者对数正态分布（Log-Normal Distribution），简单来看，当一个变量 \(X\) 服从 log-normal 分布时，其对数 \(\ln X\) 服从正态分布，反之亦然

相比于 MSE，log-normal 在预估值异常大时，loss 也不会非常大，一定程度上缓解了前面提到的 MSE 的问题

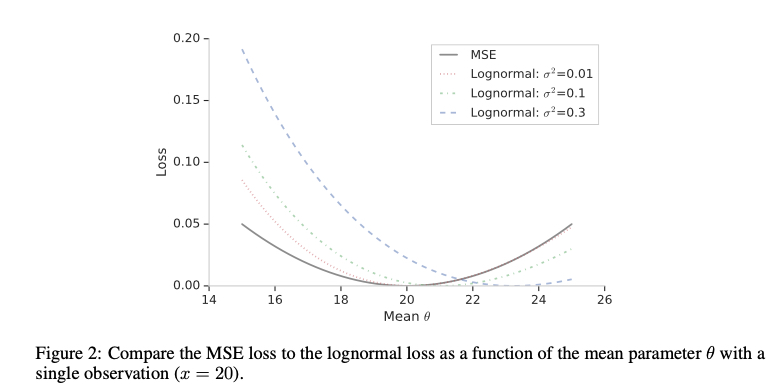
Weighted Logistics Regression

这个 loss 在 Google 这篇 2016 的神文里被应用来预估用户的观看时长，Deep Neural Networks for YouTube Recommendations；在实际业界，也有非常多的基于这个思想的 variant 和落地，相当于把回归任务转到了分类任务

从名字大概能猜到 Loss 的形式了，在一个分类的 loss 上做 reweight，具体的做法是使用 cross entropy 这个损失函数，然后对于正样本（在建模观看时长中是点击的样本），使用具体的观看时长 \(T\) 来做 reweihgt，负样本不变

做了 reweight 后，相当于改变了原来的样本中的正负样本的比例（这里把观看的作为正样本，不观看 / 点击 作为负样本），我们知道 cross entropy 最终预估的概率值是正样本的比例，而 reweight 后，对于 label 为 \(T\) 的样本，相当于在分类任务中变为了 \(T\) 个正样本

则总体样本的正样本的比例变成了 \(\frac{\sum_{i=1}^k T_{i}}{N + \sum_{i=1}^k T_{i} -k}\), 其中 \(N\) 是总样本数，\(T_i\) 则是每个正样本的观看时长，\(k\) 是正样本的数量（这里的推导过程跟 paper 里推导过程不太一样，但原理和结果是一样的，会更直观一点）

而根据 Logistics Regression 的预估值为正样本的比例可知

\[\begin{align} \frac{1}{1+e^{-logit}}=\frac{\sum_{i=1}^k T_{i}}{N + \sum_{i=1}^k T_{i} -k} \end{align}\]

由于正样本的数量往往非常少，因此 paper 把 \(k\) 省略掉，令 \(P=\sum_{i=1}^k T_{i}\), 则上面的式子变为了

\[\begin{align} \frac{1}{1+e^{-logit}}=\frac{P}{N + P} \end{align}\]

左边分子分母同时乘上 \(e^{logit}\), 右边分子分母同时除以 \(N\), 最终可以推导出 \(\frac{P}{N} = e^{logit}\), 由于这里的 \(P\) 是取了 sum 的，平均到每个样本上，最终 serving 时预估的时长的值就是 \(e^{logit}\)

则在训练时使用的损失函数还是 cross entropy，同时对正样本做 reweight，serving 时得到 logit 后，取 \(e^{logit}\) 作为最终的预估值，paper 里这张图很好地展示了这个过程

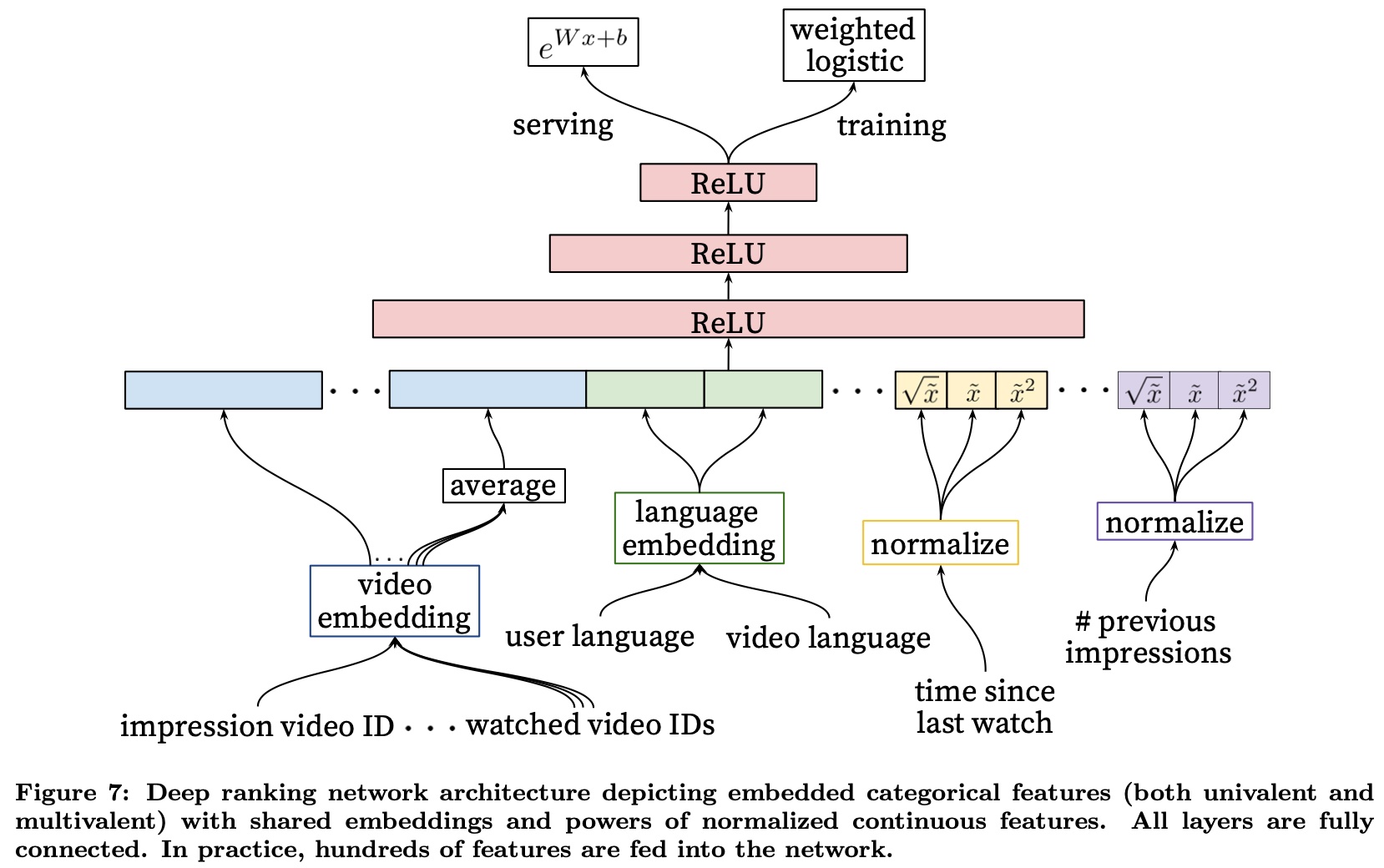
上面的推导过程中忽略了原来样本中正样本的数量 \(k\)，从严格意义来讲，这会导致预估值有偏，所以最简单的方法是对于 label 为 \(T\) 的样本，把它当做 \(T\) 个正样本和 1 个负样本，相比于原来的做法，为原来每个正样本多增加了一个负样本

则原来的公式会变成如下所示，等式右边的分母里，第一个 \(k\) 表示原来的正样本的数量，第二个 \(k\) 则表示新增的负样本的数量，这样就不用有 “正样本的数量往往非常少可省略” 的假设了

\[\begin{align} \frac{1}{1+e^{-logit}}=\frac{\sum_{i=1}^k T_{i}}{N + \sum_{i=1}^k T_{i} - k + k} \end{align}\]

回到这个 loss 的假设，我们知道 cross entropy 的假设是 label 服从参数为 \(p\) 的伯努利分布（这里的 p 为成功的概率），然后通过 MLE 可求得 cross entropy 的形式

而在 cross entropy 基础上做了如上的 reweight 后，相当于是假设了 label 服从了参数为 \(p\) 的几何分布（不是非常严谨，因为这里的 \(p\) 是失败的概率），reweight 时使用的值（即 label \(T\)），就是几何分布的 pdf 取 log 后提到前面的值，表示连续失败 \(T\) 次（这里跟原来的几何分布的物理含义刚好相反）

Bucketing With Softmax

在回归中，还有另一种套路就是分桶 + softmax，其思路也很直观，就是对 label 的值域进行分桶，然后根据每个样本的 label 把样本分到某个桶里，训练时转为一个多分类问题，通过 softmax 损失函数进行训练

serving 时利用 softmax 预估的概率分布，对每个桶做加权求和，如下式所示，\(n\) 表示有 \(n\) 个桶，\(p_i\) 表示每个桶的概率，\(v_i\) 则表示每个桶的值（往往会取桶的中值）

\[\begin{align} pred = \sum_{i=1}^{n} p_i v_i \end{align}\]

这个方法的关键在于如何分桶，包括分桶的数量和每个桶的大小，这两个变量对最终的效果影响会比较大，分桶过多，容易导致每个桶的样本过于稀疏，而分桶过少，预估值有没有区分性

一般的做法是人工根据 label 的后验分布进行划分，且由于实际中的数据往往会比较长尾（即 label 较小的样本会比较多），所以会在 label 较小的时分桶数量较多，桶的间隔也会越小，目的还是让每个分桶的样本尽量均衡；但桶的数量和大小，是需要不断调整的超参

除了直接使用桶的均值作为最终的加权求和项，还可以在每个桶都套上一个前面提到的损失如 mse 等，不过这样就相当于是分区间的 multi-task 建模了，或者说是 ensemble 中的 stacking 方法了

在这类方法中，另一个常见的操作就是 ** label smoothing**，这个方法的出发点是对于原来的方法丢掉了 label 之间的大小关系，比如说把 label=50 的样本分到 [0,10] 的桶和 [51, 100] 的桶的损失是没有区分性的，因此自然的一个想法是让原来 one-hot 的 label 变得更加 smooth

具体的思想是在训练时对 label 做变换，让其变为类似高斯分布或拉普拉斯分布的形式，比如说原来的 label 是 [0, 0, 0, 0, 1, 0, 0, 0], 对其进行 smooth 后会变为 [0, 0, 0.01, 0.03, 0.9, 0.03, 0.02, 0.01], 而这里变换的方法也相当于一个超参了

总的来说，这个方法涉及到比较多的先验知识，包括如何分桶，如何选择 label smoothing 的函数；但是避免了对 label 的先验假设，理论上适用于任意的回归任务，但是需要定期 review，防止总体数据有变，先验假设失效

Ordinal Regression

Ordinal regression 是一种适用在关注不同值的序，但不怎么关注具体的值的场景，套用 wiki 的话是这么说的

variable whose value exists on an arbitrary scale where only the relative ordering between different values is significant. It can be considered an intermediate problem between regression and classification

常见的任务比如说评级，例如针对图片、视频的色情程度做出评级，不直接采用分类的原因，跟上面提到的 bucketing 方法里的 label smoothing 一样，分到不同的桶里没有区分性，

具体的 loss 形式也是基于 MLE 来推导，但是不同于前面的算式基于 PDF
(Probability Density Function
) 做 MLE 的推导，这里采用的 CDF (Cumulative Distribution Function)，这里用了基于 CDF 的 MLE，推导过程如下图所示，从推导过程可知，这里的推导的假设也是 “误差 \(\epsilon\) 服从标准正态分布”，跟 MSE 一样

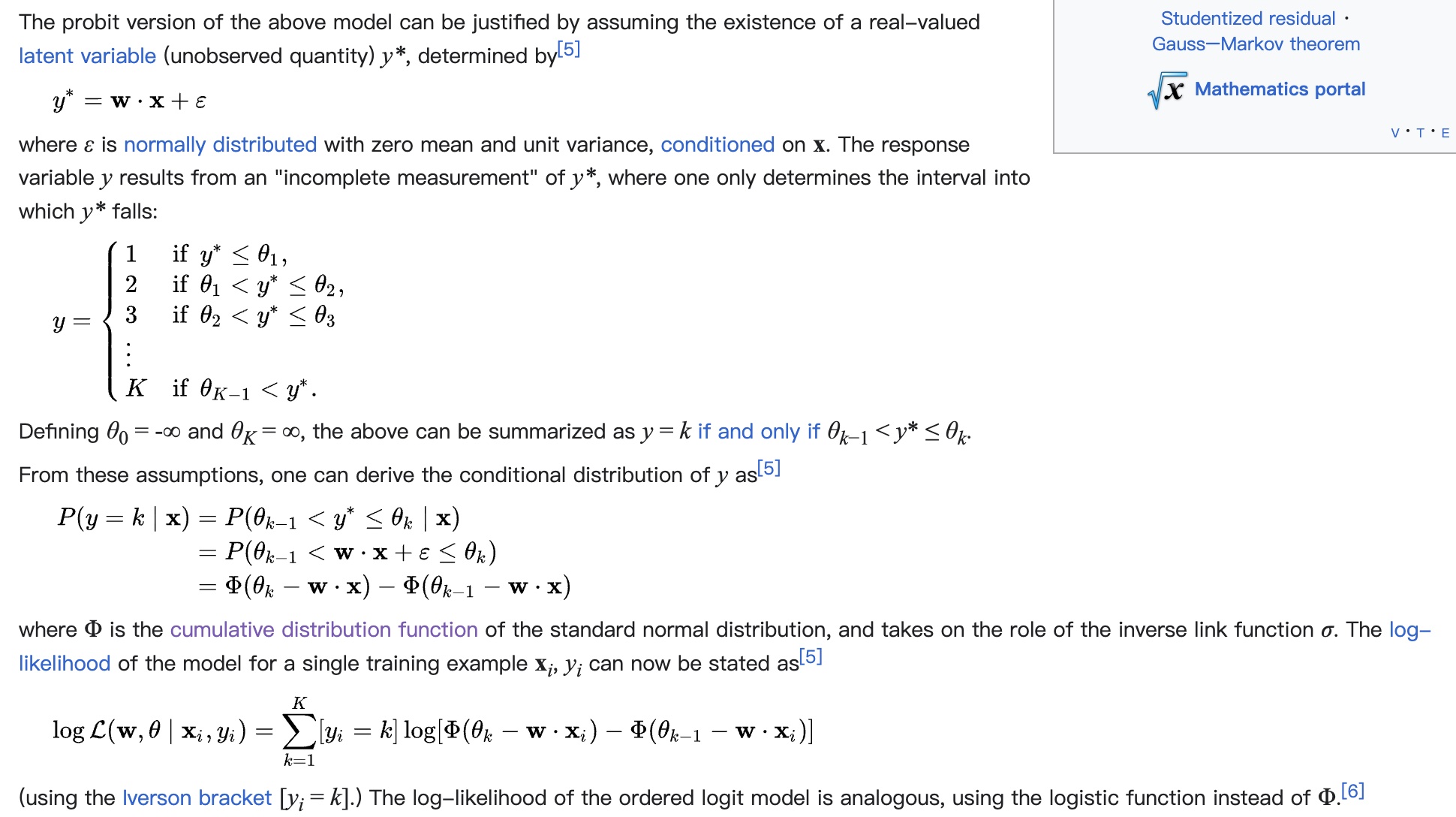
用来区分样本处于不同区间的 \(\theta\) 也是需要通过训练得到的参数，最终的 serving 输出也是依赖 \(\theta\) 和具体的预估值， 这篇文章提供了一个实现参考：处理分级问题的利器 Ordinal Regression

值得注意的是，对于评级任务，label 是比较明确的，但是对于一般的回归任务，还是存在着划分区间，或者说给每个 label 评级的过程，这个跟上面的 softmax 类方法一样，也是需要拍的超参

小结

本文主要描述了回归任务中常见的一些损失函数，每种损失函数背后的假设不相同，其适用范围也不一样

MSE、MAE、Huber Loss 是回归中比较常用和直观的回归损失，其假设是预估值和真实 label 服从正态分布或拉普拉斯分布

Log-normal 损失函数则直接假设 label 服从 log-normal 分布，通过 MLE 去求解 log-normal 的概率密度函数中均值 \(\mu\) 和方差 \(\sigma\) 这两个参数（二分类中的 cross entropy 的求解原理也是这样，只是分布改成了伯努利分布，参数改成了事件发生的概率 \(p\)）

除了直接预估，也有通过转为分类来间接预估最终的值的，主要有 2 类方法（1）Weighted Logistics regression （2）Bucketing With Softmax

Weighted Logistics regression 通过把一个 label 为 \(T\) 的样本当做 \(T\) 个正样本（和一个负样本），在统计意义上推导保证了预估的无偏，在实际中应用也较为广泛，其背后的假设是 label 服从几何分布

Bucketing With Softmax 则是通过对 label 进行先验分桶，然后通过 softmax 预估 label 落在每个桶的概率分布，最后对每个桶进行概率加权求和得到最终的预估值，这种方法的好处是对分布没有任何假设，理论上适用所有的分布，但效果非常依赖分桶的数量和桶大小，其中也涉及 label smoothing、stacking 等改进技巧

Ordinal Regression 则是一种关心序但不关心绝对值误差的回归 loss，其假设跟 MSE 一样，但是使用了 CDF 而不是 PDF 来推导最终的损失，并通过训练得到分割不同级别的阈值，一般在评级任务中较为常用；但是在更一般的回归任务中，还是会依赖人工划分区间给予不同样本不同的评级