adload 约束下的混排价值最大化
之前写的混排文章,主要介绍了《Ads Allocation in Feed via Constrained Optimization》里的基本做法,同时拓展讨论了混排中的一些开放性问题,这篇 paper 解决的问题是 request 维度的插入规则,但是没有考虑到一些比较实际的约束如 adload,即出广告的比例是有限的
而如果考虑到 adload 的约束,就不能只考虑 request 内的价值比较了,而是要考虑到 request 之间或者说 session 维度的价值最大化了,如在某些高价值请求上多出,低价值请求上少出或不出,以此达到 adload 约束下收入最大化。这篇 paper《Hierarchically Constrained Adaptive Ad Exposure in Feeds》为这个问题提供了一个解决思路;paper 整体做法还是 beam search 和 generator+evaluator 的混排范式,但是在这个过程中会把整体约束考虑到这个在线的求解过程中;相较于常规做法把控 adload 独立在混排之外,是一个比较好的思路,值得一读~
问题建模
定义
paper 把整体问题定义如下

其中有两点值得注意
- 价值度量
价值度量或者说量纲对齐,是混排阶段无法绕开的问题; paper 里推荐候选的用户价值即 \(U^{rec}(s|\pi_s)\) 和广告的商业价值即 \(U^{ad}(s|\pi_s)\) 量纲的对齐,还是用一个货币化超参 \(\alpha\) 来做的
这也是业界常见做法,究其原因,应该还是商业价值(ecpm)有比较明确的物理含义,且不容易突变(因为 bid 基本稳定、ctr、cvr 预估也有准确性要求),像推荐往往只关注序不关注高低估,这可能导致的问题是推荐的分一旦抖动时,容易导致出现积压,所以往往也会对推荐分做一些稳定性的保障,如 cap 掉异常值,整体做归一化等
- application level 建模
如背景提到的,前一篇 paper 主要在于建模的是 request-level 价值的最大化,但没有考虑到有 adload 约束(即下图的 \(m^*\))的时的情况,而这里建模时会把一个 session 的 request 共同考虑
建模
上面的问题虽然定义起来比较简单,但是如果要直接求解 \(\pi\) 还是比较难的,所以还需要对问题做一些转化,转换成数学上可求解的形式,具体的方法是把整体的策略拆解成两部分,分别是 application-level 的策略 \(x\) 和 request-level 的策略 \(\pi\), 如下所示 \(x\) 解决否在这个请求出广告,而 \(\pi\) 解决在这条请求出多少广告;除了这两个符号,paper 使用的符号定义如下
在 reqeust 维度定义了出广告的价值 \(v\) (\(\pi_0\) 表示不出广告)和广告数量 \(w\) ,如下所示;这里有个点 paper 里没有说得很清楚,就是 \(v\) 的详细计算方式,乍一看下面的公式(4),\(v\) 就是广告的价值之和,最直观的方式就是纯广告候选的 \(\sum ecpm\),但这种方式是考虑不全的,一是只考虑了商业价值, 二是广告插入后对推荐内容的影响没被考虑在内
猜测实际的计算方式应该是:同时出推荐内容和广告的 list 价值 - 只有推荐内容的价值 , 这也意味着在 beam search 中每个 list 的价值时,需要同时计算两个,即有广告的 \(U(s|\pi_s)\) 和无广告的 \(U(s|\pi^0)\);另外,paper 这里也没给出具体的 \(U(s|\pi_s)\) 和 \(U(s|\pi^0)\) 计算方式,实际的计算应该还要考虑位置的衰减,即需要乘上 position_discount

在 adload 约束下的价值最大化,其实就是一个典型的 0-1 背包问题,adload 就是背包的容量,需要最大化出广告的请求的价值,则基于上面定义的符号,可以写出下面的最优化稳定的定义,\(x_s\) 就是某条请求是否要出广告

但与传统背包算法不同的点是,物品的价值是会动态变化的,即由 request-level 的策略 \(\pi_s\) 决定的,因此 paper 设计了 two-level 的算法来优化这个问题,一个是 application level,一个是 request level
问题求解
application level
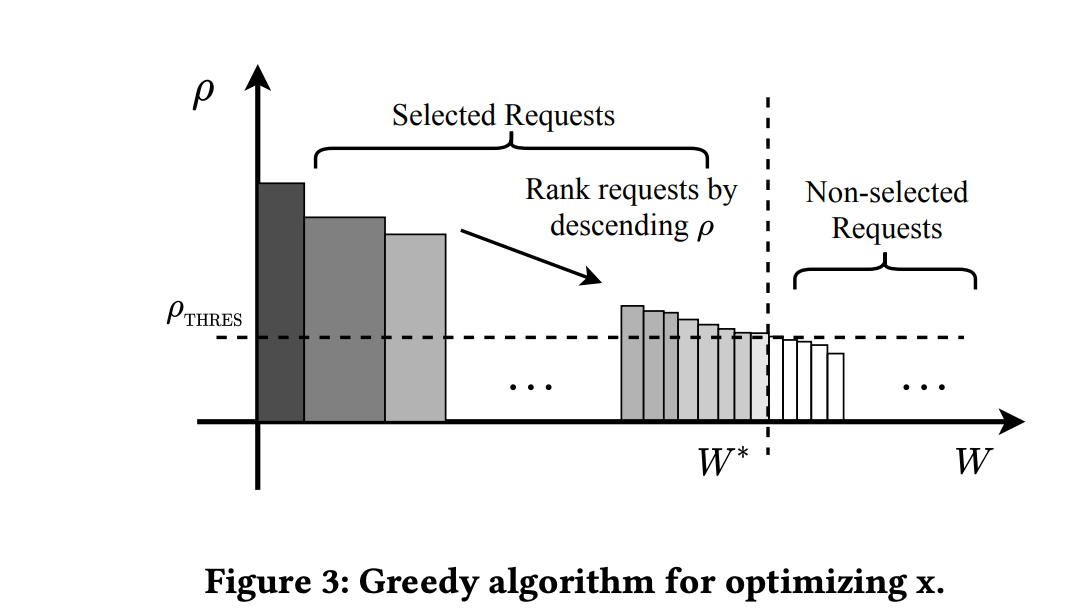
这里是通过贪心算法求解 application-level 的问题的,即决定当前请求是否出广告(ps,贪心算法求解背包问题非最优,但足够轻量级),具体做法就是基于上面定义的 \(v\) 和 \(w\) 计算 \(\rho = v/w\) (可以理解为广告的边际价值),然后基于 \(\rho\) 排序,然后在 adload 的约束下求一个 \(\rho\) 的门槛,线上 serving 时只有门槛大于这个的请求才能出广告,如下图所示
request level
request level 要决定的就是具体出广告的策略 \(\pi_s\)
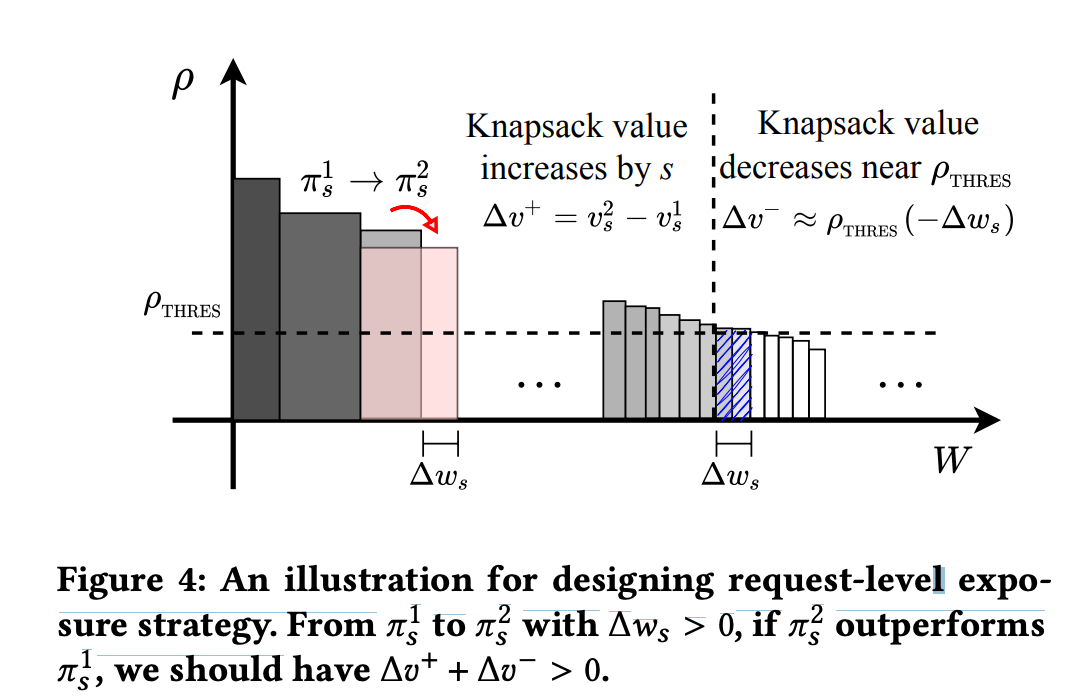
假设出广告策略从 \(\pi_1\) 变到了 \(\pi_2\),相应的这个请求的 \(v\) 和 \(w\) 都会发生变化(记为 \(\Delta v^{+}\) 和 \(\Delta w_s\)),而由于 \(w\) 发生了变化,会导致其他请求会多出或少出广告,进而影响 application-level 的价值
如下图所示,在这个请求内增加的价值的为 \(\Delta v^+\),但是其他请求减少的价值为 \(\Delta v^-\)(近似值,用上面求出来的请求门槛近似减少的广告的价值,极端情况下不一定成立),而只有这两者加和大于 0 时,这个策略才是有效的
而如果对 \(\Delta v^{+} + \Delta v^{-} > 0\) 做展开,可以得到下图的公式 (10),而根据公式 (10) 可以得到得到最优的 \(\pi_s\) 的思路是要找到一个 \(\pi_s\),使得 \(v(s|\pi_s) - \rho_{thres} * w(s|\pi_s)\) 最大,即下图(11)
这是非常关键的一步,能够把一个跨请求的优化转为当前请求就能解决的优化的问题,因为 \(v(s|\pi_s)\) 和 \(\rho_{thres} * w(s|\pi_s)\) 都是当前请求就能得到的值

保序问题
混排中另一个常讨论的问题是,是否要对输入的队列保序;即输入的推荐队列和广告队列在混排后,内部是否保序,如广告队列 [A1,A2,A3] 在混排后,内部保序意味着整体队列会长这个样子 [...A1...A2...A3...]
直观来看,保序有两点比较重要的意义 (1)不影响各链路精排的迭代,即精排 auc 的指标的迭代是有效,而如果在混排改了精排的序,是有可能导致精排 auc 的不可读 (2)对于广告扣费,需要保证广告排序时按照 sorted_ecpm 降序排列的,否则扣费会有问题
paper 则从拍卖机制出发,从 Incentive Compatibility (IC) 和 Individual Rationality (IR) 强调了保序的重要性
IC 就是常说的激励兼容,具体来说,一个机制是激励兼容的,意味着当且仅当每个参与者在这个过程中真实表达自己的偏好时,能获得的效用比边际要更高,即这个机制就是鼓励参与者表达真实的价值预期,放在广告里就是 bids truthfully。IR 直译过来就是 “个体理性”,指的是每个参与者在参与拍卖机制时,其效用不低于不参与拍卖时的效用,即参与拍卖不会使参与者变得更糟,这两者的联系,用 paper 的话是这么说的
Formally, if every participant advertiser bids truthfully (i.e., bids the maximum willing-to-pay price), IR will guarantee their non-negative profits, and IC can further ensure that they earn the best outcomes
那为什么这个跟保序有关?其实跟上面说的扣费原因是一样的,因为一旦破坏了序,意味着扣的钱就会发生变化,而这会破坏上面提到的 IC 和 IR,更严格的理论可参考 Myerson–Satterthwaite theorem, 这里不再详细展开
但是混排也不是完全不能改精排的序,因为混排有很多精排感知不到的 context 信息(如上下文的推荐内容、位置等),因此在混排基于 context model 重新预估 ctr、cvr(相当于让 ctr、cvr 预估更准确),这种情况也是有可能改序的,但这种改序的同时也改了 ecpm,也保证了 ecpm 是递减的,也不违背上面说的问题,这种方式也是笔者认为在混排改序唯一合理的方式
混排算法
整体的算法还是基于 beam search 的框架来做,如下图所示,下文的 exposure template,均指的是基于 beam search 搜出来的候选 list
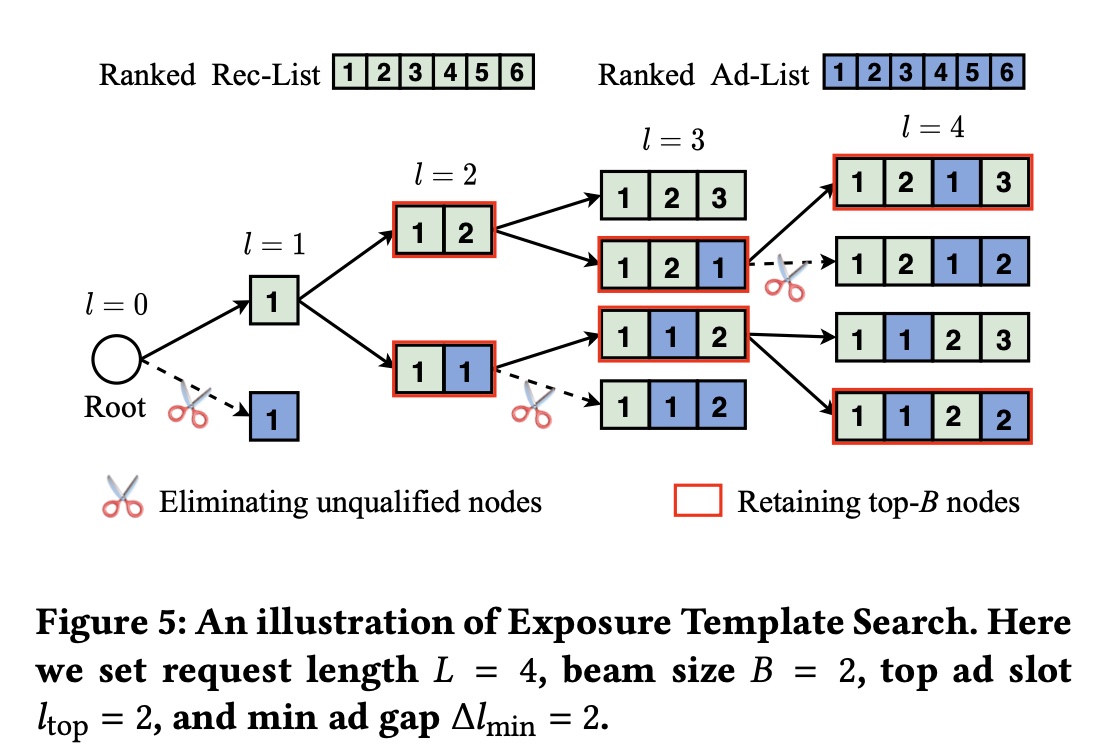
整体的算法如下图所示,第 6 行和第 9 行的公式 14 ,其实就是上图的公式 12,即找到 \(v(s|\pi_s) - \rho_{thres} * w(s|\pi_s)\) 最大的候选 list;12 是对当前候选做剪枝,即把候选中突破了红线约束(如 mingap)的候选排除,减少计算复杂度;13-14 行的含义是选择当前价值最大 \(B\) 个候选 list 进入下一步的 search,比较标准的一个 beam-search 算法

而在 beam search 最终选择出来的候选中,最终决定是否要插入广告,会基于上面提到的 application-level 求解出来的价值门槛 \(\rho_{thres}\),如下图所示
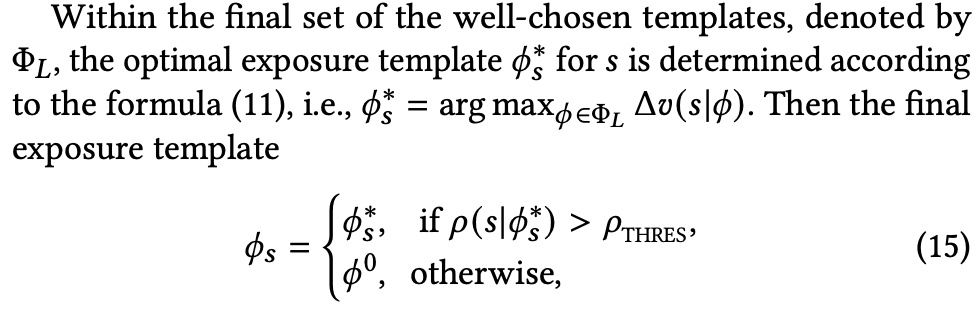
一个值得注意的问题是 \(\rho_{thres}\) 的求解频率,如果做天级更新,即根据过去 n 天数据计算一个 \(\rho_{thres}\) 然后在当天保持不变,容易出现的问题是当前流量如果有波动,容易导致 adload 超或打不满;一种解决方法是提高求解 \(\rho_{thres}\) 的频率,同时使用更实时的数据来求解(eg 每小时求解一次,用过去 n 个小时的数据),另一种解决方法就是在输出的 \(\rho_{thres}\) 基础上再叠加一个 pacer,调控实时的 adload,即当 adload 超了就提门槛,反之降门槛(跟常见的调控 sorted_ecpm 门槛控制 adload 一个道理)
小结
paper 在当前业界广泛使用的 “list 价值评估 + beam-search” 的混排框架下,考虑了在 adload 约束下,整体价值(自然 + 广告)最大化的问题;相较于更常见的仅考虑广告侧信息控 adload 的方法(如调整 ecpm 门槛),有创新的地方,而除了 adload 约束,其他的约束也可以考虑利用这套建模和求解方法,来融入到整体的混排算法中