Multi-channel Budget Allocation and Bidding
最近一段时间在研究 multi-channel bidding 的问题,套用 Google Ads 的 Power More Conversions and Value through Cross-Channel Bid Optimization 是这么定义这个问题的
Traditionally, advertisers have applied automated bidding to campaigns that target a single channel. For example, they might use a bid strategy that maximizes conversion value on separate campaigns for Search, Display, and Video. But there are limitations to this siloed approach. But multi-channel bid optimization can help you to drive better results compared to single-channel bid optimization by maximizing marginal CPA or ROAS in each and every auction
简单来说,就是一个计划在更多流量位上同时投放,能够更好优化预算的边际收益(marginal CPA or ROAS),这个也很好理解,因为有了更丰富的流量库存,同一笔预算效率理论上是能做到更优的;这跟国内当前各个媒体平台近年提的 “通投”、“全站投放” 等产品,本质上也是类似的。这类产品广告主提供了使用门槛更低的产品,省去了广告主在不同 channel 分配预算或设置出价的过程,同时平台能够通过算法能力把预算的效率变得更高
从技术视角上来看,这里的 multi-channel 有两个问题值得讨论
(1)统一出价是否是最优的?如果不是,分 channel 出价要怎么做
(2)预算是否要显式分配到各个 channel
上面讨论的 multi-channel 的例子都是在一个大的平台下的 channel,这种情况下各 channel 的预算和出价是比较容易共享的;而另外一个常见的 multi-channel 的定义是跨平台的,比如说很多广告主会同时在 google 和 meta 两个 channel 投放,这个时候显然预算和出价是不能共享的;那站在广告主的视角下,怎么分配是最优的也是一个值得讨论的问题
本文主要讨论前者,即在同一平台的多个 channel 同时投放时,budget allocation 和 bidding 的相关问题;同时会提一下在不同平台(channel)投放时的一些研究,祝开卷有益~
上面提到,在同一平台上的多 channel 投放,有两个问题需要解决,一是出价,即是否要分 channel 独立出价;二是预算分配,即是否要限制各个 channel 使用的预算,下面分别谈一下这两部分
统一出价 vs 分 channel 出价
在 multi-channel 中常见的一个问题是,统一出价(即在各个 channel 中使用同一个出价)是否是最优的
直观来看,把所有 channel 当做一个整体的广告位,然后统一来出价似乎是比较合理的?但如果进一步分析,结论不一定如此;可以粗略把出价产品分为成本类出价和非成本类出价
对于成本类出价(如 target-cost、cost-cap),往往是基于后验做 bidding,这一做法本质上是在为模型预估不准做兜底;当各个 channel 的模型预估准确时,统一出价是最优的,但这一点往往很难成立,更常见的情况是在 channel A 高估,在 channel B 低估,或者高估程度不太一致;而如果仅靠一个统一的出价,无法很好处理各个 channel 高低估不一致的问题,比如说统一提价能解决低估的 channel 问题,但是会加剧高估 channel 的问题
非成本类出价(如 lowest-cost)没有上面的问题,但非成本类往往会通过 budget allocation 来间接控制成本,而 budget allocation 曲线的一个很重要的信号就是 channel 的流量分布,会倾向于把预算更多分配到流量更多的时间片,而各个 channel 的流量分布往往是不一致的,即各个 channel 的最优预算分配曲线往往也是不一致的
因此,无论是成本类出价还是非成本类出价,比较合理的的做法往往是各个 channel 独立出价,而这又有常见的两种方式
(1)所有 channel 的出价都独立,即独立搜集数据,独立 pacing
(2)基于所有 channel 的后验计算出一个基础的出价,然后各个 channel 基础的出价上再做扰动
选择哪种方式,也跟出价类型、数据稀疏程度等因素有关
成本类出价理论上两种方式都可用,如 target-cost 和 cost-cap 这一类产品,广告主是有明确的成本目标 / 限制的,各个 channel 只要锚定广告主明确的诉求,其实就可独立做出价,这里还有个问题是数据的稀疏程度,方式(1)有效的前提是各个 channel 的后验数据都比较充足,否则数据过于稀疏冷启问题会比较严重
而对于 lowest-cost 这一类非成本类出价的产品,使用方式 1 就有点困难了,主要原因有两个
一是方式 1 要求每个 channel 的预算是明确的,但这在通投场景是没有的(可通过算法分配一个,后面预算分配会提到)
二是 nobid 虽然没有明确的成本约束,但是 channel 之间的成本差异不能过大,一个很直观的想法是,成本更高的 channel 向成本更低的 channel 的成本看齐,这样会就是一个动态的 target-cost 产品,且预算花完是没有保证的;因此实际中往往是一个主 channel 负责把钱花完,其他 channel 把成本对齐主 channel
综上,这部分基本的观点是分 channel 出价在实际中往往是更优的,而分 channel 出价是否要做到各 channel 完全独立,取决于多种因素。在广告主明确表达了成本的产品上,理论上是可以做到完全独立出价的,但需要各 channel 后验数据充足;lowest-cost 因为没有显式的分 channel 预算,做独立出价有点难,最直观的做法是在主 channel 的出价基础上做一些扰,做成一个动态 target-cost (主 channel 的成本)的产品,后面也会提到的一个做法是在不同 channel 之间做预算分配
预算分配
预算分配跟出价是紧密相关的,尤其是对于 lowest-cost 这一类出价,预算分配是最主要的调控手段;这里的预算分配的主要问题是预算是否要显式分到各个 channel;而这部分的做法同样跟具体的出价类型相关
成本类出价
对于 target-cost 或 cost-cap 这一类有广告主明确的 given_cpa 的出价,由于是有明确的成本目标,理论上是可以共享预算,即各个 channel 都锚着固定成本去 pacing 后验成本达到这个目标,这种情况下不需要对预算做显式的划分,哪个 channel 能在 given_cpa 的约束下能花更多的钱,这个渠道就是更优的;不过共享预算 + 基于后验 pacing 的 target-cost 也有一些其他问题
除了上面说的数据稀疏,基于后验成本 pacing 的成本类出价一直面临的另一个挑战是,后验数据回传延迟(delayed feedback)问题,这个问题会导致当前计算的后验成本不准确,往往需要建模来解决(模型也会面临这个问题,关于这个问题的一些解决方法可参考 Delayed FeedBack In Computational Advertising)
也有业界的做法是做了预算的划分的,比如说这篇 paper 《Spending Programmed Bidding: Privacy-friendly Bid Optimization with ROI Constraint in Online Advertising》,就是对成本类出价的预算做了划分,并且通过实验验证效果是更优,文章建模的思路挺值得学习的
SPB 大致的做法就是先基于后验数据(不一定要非常实时,整体还是要考虑数据的时效性与有效性的 trade_off),离线建模 cost2convert 的函数,然后基于 given_cpa 计算一个 budget,最后基于预算分配曲线把 budget 花完,这样理论上收到上面的影响会更小,paper 中的是这么说的
SPB is a two-stage framework that separates long horizon delivery spend planning (the macro stage) and short horizon bidding execution (the micro stage). The macro stage models the target ROI to achieve maximum utility and derives the expected spend, whereas the micro stage optimizes the bid price given the expected spend.
这个方法的关键点是建模 cost2convert 的函数 \(f(cost) = convert\),常见的一个先验假设是随着 cost 增加,转化数的增加速度逐渐减小,或者说边际成本是逐步增加的,如下图所示(横轴是消耗,纵轴是转化数);这个假设也比较直观,因为对于一个计划而言,便宜的转化拿完了,需要出更高的价才能拿得到转化,转化成本是随之增加的
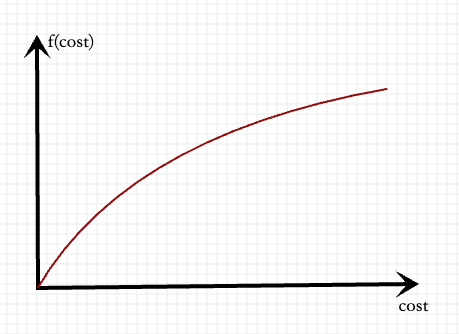
根据上面的定义,可以得到成本的公式为 \(\frac{cost}{f(cost)}\), 而边际成本则是上面曲线的斜率的倒数即 \(\frac{1}{f'(cost)}\),基于上面的边际成本随着 cost 逐步增加的假设,可以进一步假设边际成本与转化数 \(f(cost)\) 成线性关系(实际中不一定是线性,保证是递增的关系即可), 如下所示,其中 \(\omega\) 和 \(b\) 是需要拟合得到的参数
\[\frac{1}{f'(cost)} = \omega * f(cost) + b\]
通过如下推导

可以得到 \(f(cost)\) 的形式为 (这里省略了常数 \(C\), 且因为 \(f(cost)\) 不会为负数,因此只取了为正数的那一项)
\[f(cost) = \frac{\sqrt{2 * \omega * cost + b^2} - b}{\omega}\]
上面的推导,其实也可以直接基于边际成本上升直接给 \(f(cost)\) 一个先验的函数形式, 这里是直接对斜率做了假设然后推导的,但其实跟直接的假设没有多大的本质区别
利用客户给定的 given_cpa, 可以得到下面的等式
\[given\_cpa = \frac{cost}{f(cost)} = \frac{\omega * cost}{\sqrt{2 * \omega * cost + b^2} - b}\]
进一步求解上面的方程可得到分配的预算为
\[cost = \frac{(2 * given\_cpa - b)^2 - b^2}{2 * \omega}\]
因此,只要通过历史数据拟合得到 \(\omega\) 和 \(b\),就能沟通过客户给定的 given_cpa 得到规划的预算
上述的方法应用到多个 channel 的情况,可以为每个 channel 拟合出自己的 \(\omega\) 和 \(b\),然后基于上面公式来计算每个 channel 应该分配的预算
但这种方式也有其局限性,首先这种建模的精度不一定是非常准确的(因为如果能够准确建模出 cost2convert 的关系,相当于可以预估计划的实际成本了);其次是假设的先验形式,在实际中不一定是所有的计划都服从这样的形式(分段线性拟合的能力理论上要比这种纯先验的要好一些),甚至不都服从随着 cost 增加,边际成本上涨的假设;其次是由于 cost2convert 对转化数有要求,因此在 convert 数不足时,需要走探索出价,只有在转化数置信后才能建模
非成本类出价
在统一出价中提到,对于 lowest-cost 这一类非成本类出价的产品,使用完全独立出价有点困难了,主要原因是这种方式要求每个 channel 的预算是明确的,但这在通投场景是没有的明确的预算分配,那能不能通过算法算出一个? 我们在上面的 SPB 的 paper 里提到的计算过程,不就是一个分配预算的过程么?能否复用上面的方法呢
对于 lowest cost 这类没有广告主给定的出价,没有 given_cpa,理论上没法直接套用上面的那种模式;但我们能否给定一个 margin_cpa 作为 given_cpa,然后做到预算花完的前提下 margin_cpa 最小?答案是可以的,首先看上面 cost2convert 的形式
\[f(cost) = \frac{\sqrt{2 * \omega * cost + b^2} - b}{\omega}\]
如果直接看这个函数,大概长下面这个样子的;从红线到黑线,代表 \(\omega\) 从 1 变成了 3,\(b\) 不变,从红线到绿线,代表 \(b\) 从 1 变成了 5.2, \(\omega\) 不变,两者在花相同的 cost 前提下,转化数都更少了,即转化成本上涨了
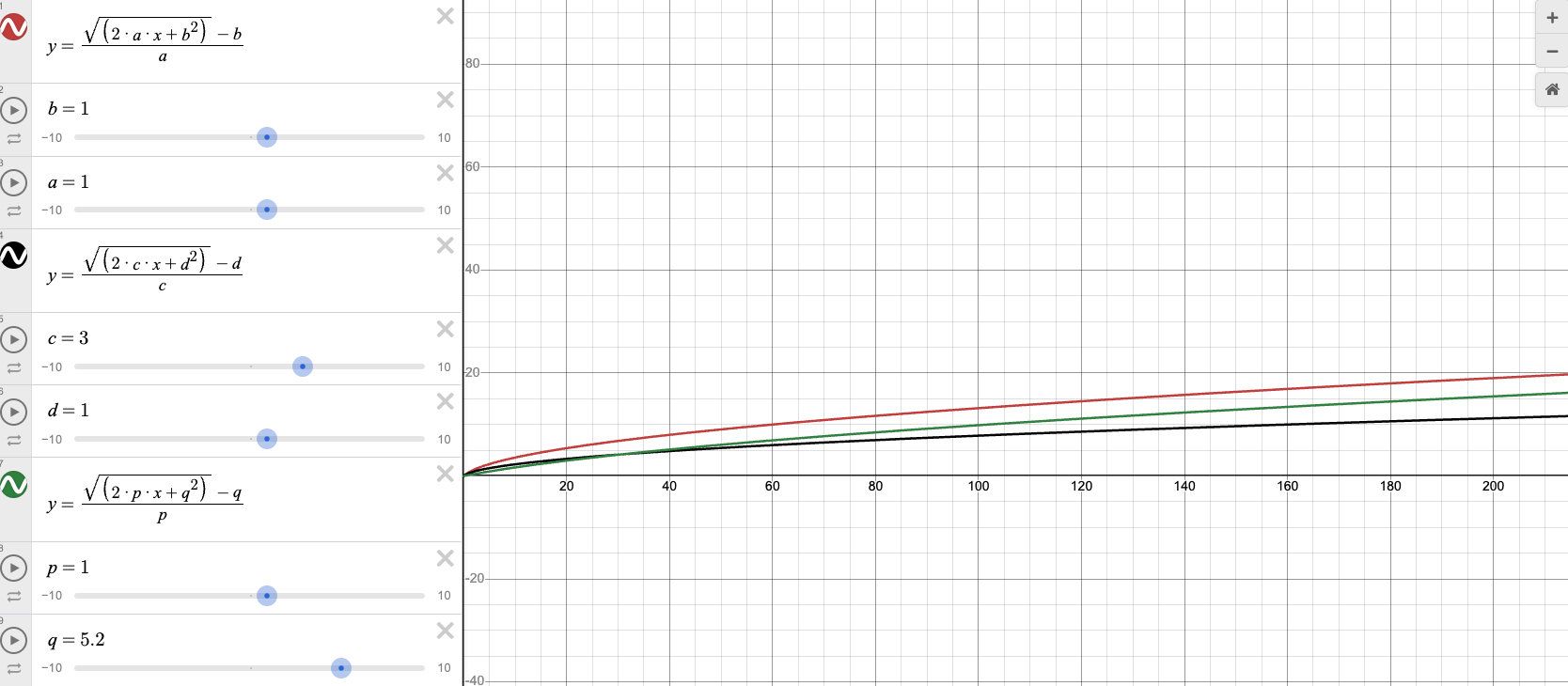
因为前面的推导中有个假设是边际成本与转化数 \(f(cost)\) 成线性关系(如下所示),则 \(\omega\) 和 \(b\) 的上涨就代表了成本的上涨,或者说每个 channel 拟合出来的 \(\omega\) 和 \(b\) 代表了其转换成本的高低情况,\(\omega\) 和 \(b\) 越大,代表成本越高
\[\frac{1}{f'(cost)} = \omega * f(cost) + b\]
而从最终的预算分配公式可知,一个 channel \(\omega\) 和 \(b\) 越大,分得得预算会越少,代表整体算法会把预算更多分配到成本更低的 channel 上
\[cost = \frac{(2 * given\_cpa - b)^2 - b^2}{2 * \omega}\]
同时从上面的公式可知,\(cost\) 和 given_cpa 是正相关,given_cpa 过低,能够花出去的钱也少,因为便宜的转化就那么多;有了这个单调性的特性,就可以通过二分查找的方式来找个一个最小的 margin_cpa,使得预算能刚好花完
基于这个查找到的 margin_cpa,便能够套用上面公式计算出各个 channel 的 budget,然后基于这个分配好的 budget,lowest-cost 这类出价能够很自然地做预算分配来出价投放
跨平台的 multi-channel
上面说的都是在同一个平台的 multi-channel 的预算分配和出价,也有一些研究是针对多平台的 multi-channel 的预算分配
这篇 paper 《Multi-channel Autobidding with Budget and ROI Constraints》 就是站在广告主视角下,如何通过设置各个 channel 的 budget 和 roi 来达到营销效果的最优(这也是广告主唯二影响他们投放效果的手段)
论文的篇幅比较长,这里重点说一下论文的一个核心结论:Solely optimizing per-channel budgets are sufficient to maximize conversion,即只优化各个 channel 的 budget 便能做到 max conversion,理论证明过程比较复杂,这里就不详细展开了,套用 paper 的话是这么说的
In Theorem 3.2 of Section 3, we show that solely optimizing for per-channel ROIs is inadequate to optimize conversion across all channels possibly resulting in arbitrary worse total conversions compared to the hypothetical global optimal where advertisers can optimize over individual auctions. In contrast, in Theorem 3.3 and Corollary 3.4 we show that solely optimizing for per-channel budgets allows an advertiser to achieve the global optimal.
在上面的结论基础上,paper 设计了一个算法,用于做各个 channel 的预算分配,整体算法流程如下图所示

这个算法结合了 SGD 和 UCB,整体目标是在 budget 约束下最大化总转换数;这里基本就是套用了 Multi-Arm Bandits 的范式,将连续预算空间离散化为有限臂(候选预算值),然后基于 MAB 的探索与利用机制:迭代选择臂、观测反馈、更新统计信息,优化预算分配策略;不同的点是引入了对偶变量和 sgd(上图的公式 10),用来处理预算约束,传统的 MAB 没有涉及到这一点
但是回到实际中,对于各类广告主尤其是 SMB 这种中小广告主,如果想直接用这个方法是比较困难的,因为使用门槛会比较高;而实际中,广告主往往会先在各平台投一小笔钱看效果,然后根据各平台效果再决定在哪个平台投入更多的预算,这其实跟上面的 SGD_UCB 算法的模式也比较像,只是精度没有那么高
小结
本文主要讨论了同一平台下 multi-channel 下的出价和预算分配问题;无论是成本类出价还是非成本类出价,比较合理的做法往往是各个 channel 独立出价;而对于成本类出价或非成本类出价,都有两种技术范式,选择哪种基本得看哪种更适合当前业务现状,而这基本又得靠实验来决策了
对于成本类出价,理论上是可以共享预算,然后独立 channel 来搜集数据和出价;但除了这种方式,另一种技术范式就是类似 Spending Programmed Bidding 这种算法:通过建模 cost2convert 的关系,然后基于 given_cpa 在不同 channel 之间做显式的预算分配
非成本类出价同样也有两种技术范式,一种是共享预算,然后以一个主 channel 的成本作为后验成本,当做一个动态 target-cost 产品;另一种也是借鉴类似上面的预算分配的思路,通过搜索出一个 margin_cpa,套用同样的算法,来在不同 channel 之间做预算分配,然后基于预算分配曲线来投放