搜索相关性:从建模到排序机制
最近一段时间在研究搜索的相关性问题,一个颇有搜索特色的问题。搜索场景下的相关性,指的是展示给用户的内容,跟用户输入的 query 必须满足一定的关联关系,比如说搜 “肯德基”,就不应该出现 “麦当劳” 的内容
不同于在 feed 场景下,用户对内容基本无预期,feed 场景的推荐算法可以基于用户历史浏览兴趣、最近热点内容等做 exploit,或是通过探索用户的一些新兴趣做 explore。但在 search 场景下,用户主动搜索输入的 query 往往是有强意图的,出的内容也是要符合用户的这个预期的,否则这些搜索就是无效的,进而会造成搜索留存(LT)的损失。而在用户视角下,如果平台搜索的算法做得足够好,应该在第一页就能够找到自己想要的内容,而这这其实也导致了单 pv 下 search 浏览深度会远比 feed 要低
场景上的差异,会导致 search 相较于 feed 的优化目标也有不小差异。比如说搜索 LT 的度量中,时长并不是最重要的指标;从排序角度,增加了相关性的约束,导致特定 query 下可被用来排序的候选有限(相较于 feed),同时排序公式中往往也要加入相关性因子来达成相关性目标,对最大化原目标(如广告就是收入)的效率造成干扰
排序的相关性约束,也是导致了很多在 feed 下有效的 ranking 迭代,在 search 中效果不优甚至无效的原因,比如说这个问题里提到的现象 为什么搜索系统技术文章很少,但推荐系统技术文章很多?,一个很重要的原因是给定 query,相关性候选不足导致了 ranking 搜索空间不足,而 ranking 本身的收益应该是随着候选量增加的边际效率是递增的
本文主要探讨下搜索场景下的相关性问题的解决思路。如果粗略地划分,相关性往往会涉及到两部分:相关性的建模,以及相关性模型预估分的作用机制,本文尝试对这部分的内容详细展开做一些讨论
相关性建模
如何判断 query 与内容是否相关?直观来看可以分为主观和客观两类指标
- 客观指标:就是看一些可基于用户行为来统计的客观指标,如用户搜索后的点击率(一般叫 “有点比”,越大越好)、或者在同一个搜索意图下是否频繁换 query(一般叫 “换 q 率”,越小越好)、以及用户的搜索行为是否在减少 (搜索 LT30)
- 主观指标:就是偏人工评估的指标,一般依赖约定好的标准,定义某个 query 下不同内容的相关联的程度,然后人工定期抽检判断当前的搜索的内容的整体相关情况;但这个标准一般在不同 APP 是不一样的,即使在同一 APP 内这些标准也是会频繁发生变化的
这里说的相关性建模,针对的是主观指标的建模,而主观指标其实也可以理解为是客观指标的一类中间指标,因为往往是由于搜索结果的相关性不足,导致了用户不点击或频繁换 query 重新搜索,甚至离开平台不再搜索
演进路线
从技术视角来看,判断 query 与 doc 内容是否相关,也经历了几个阶段变化,在文章《大众点评搜索相关性技术探索与实践 - 美团技术团队的文章》中就提到了这相关性建模的演进路线
阶段一:文本匹配。仅考虑 query 与 doc 的字面匹配程度,通过 TF-IDF、BM25 等基于 term 的匹配特征来计算相关性。这种方式计算效率高,但是泛化性比较差,匹配规则比较硬,没法处理一次多义或多词一义的问题
阶段二:传统语义匹配模型。这种做法不像文本匹配那么粗暴了,而是对于原始的 query 和 doc 做一个映射,映射到一个隐式的向量空间,然后在这个空间内计算 query 和 doc 的相似性;最常见的做法就是把 query 和 doc 都映射成一个 embedding,然后基于 embedding 计算向量距离或空间相似度作为得分(实际上双塔 DNN 模型隐式地做了这个事情)。比如说 Partial Least Square Regression 这一类方法;或者是将 Doc 映射到 Query 空间后进行匹配或计算 Doc 翻译成 Query 的概率,典型的方法可以参考这篇 paper Clickthrough-Based Translation Models for Web Search: from Word Models to Phrase Models
阶段三:深度语义匹配模型。这里相较于阶段二引入了深度神经网络模型 DNN。同时可以被粗略分为两种范式:基于表示(Representation-based)的方法及基于交互(Interaction-based)的方法
- Representation-based 方法
最常见的例子是类似 DSSM 这一类双塔模型,也是召粗环节最常见的建模范式,基于 Bert 等 encoder 结构,将原始的文本等特征映射至向量空间,再通过余弦相似度或点积计算最终相关性。在微软的 Bing 搜索的 NRM 模型中,doc 的特征除了基础的标题和内容,还考虑了其他多源 (Field) 信息,如外链、用户点击这个 doc 的历史 query 等;所以在 Doc 中有多个 Field,每个 Field 内又有多个 Instance(文本,如 Query 词)。模型首先学习 Instance 向量,将所有 Instance 的表示向量 pooling 得到一个 Field 的表示向量,将多个 Field 的表示向量 pooling 得到最终 Doc 的向量,如下图所示
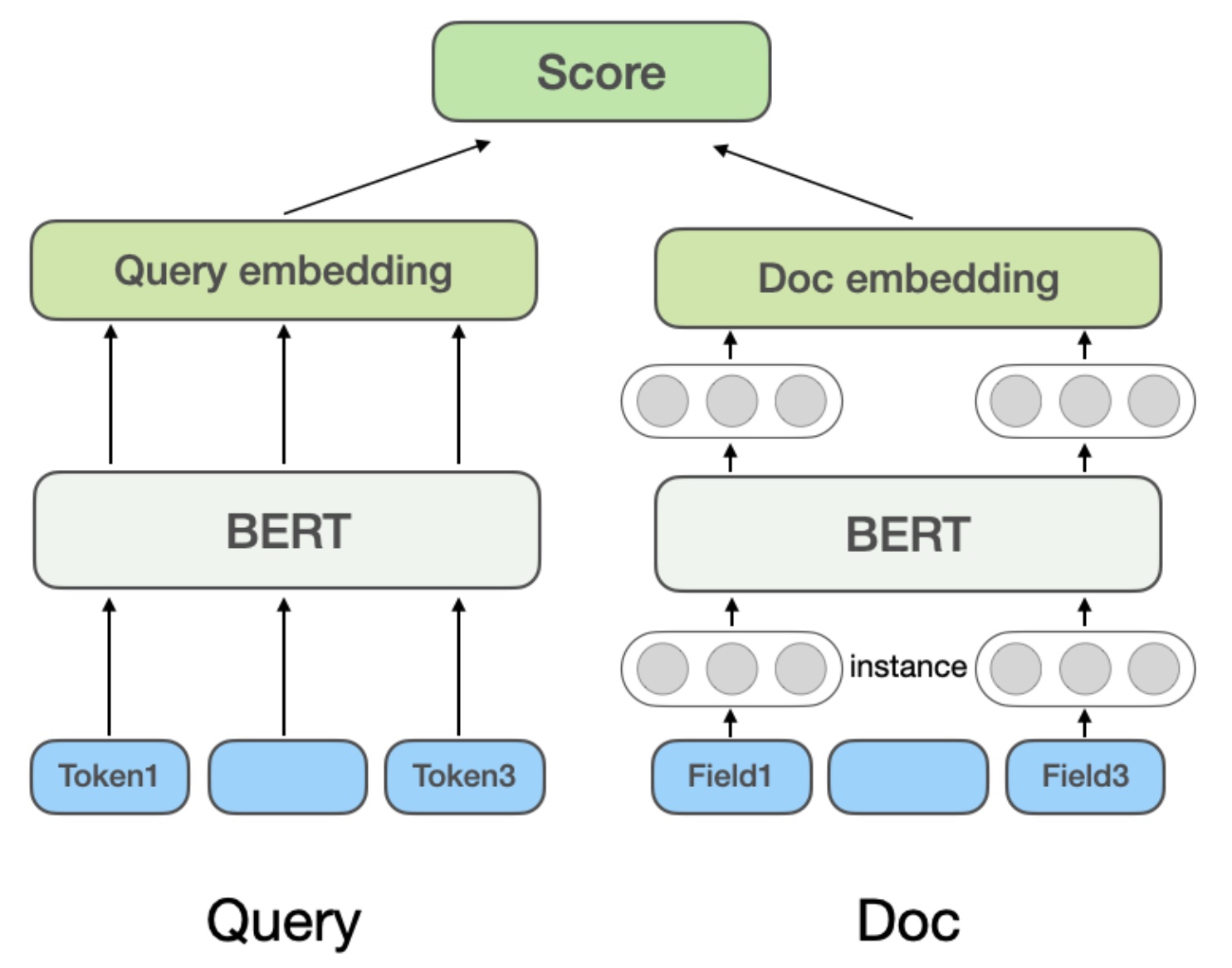
Representation-based 方法的好处是 doc 的向量可离线计算并缓存,线上服务时仅需计算 Query 向量并进行简单的相似度计算,性能好,延迟低,但缺点是 Query 和 Doc 在编码过程中缺乏直接的交互信息,仅依靠最终向量进行相似度计算,可能会丢失一些细粒度的匹配信号,表达能力有一定上限
- Interaction-based 方法
这种方法没有显式将 Query 和 Doc 分开来直接学习 Query 和 Doc 的语义表示向量,而是在底层输入阶段就让 Query 和 Doc 进行交互,如果说前面的双塔是召粗常用的范式,这里的模型是精排常用的范式。ESIM是预训练模型引入之前被业界广泛使用的经典模型,首先对 Query 和 Doc 进行编码得到初始向量,再用 Attention 机制进行交互加权后与初始向量进行拼接,最终分类得到相关性得分
而引入预训练模型如 BERT 后,通常将 Query 和 Doc 拼接作为 BERT 句间关系任务的输入,然后输入模型得到最终的相关性得分,如这篇 paper 的做法就是这样的 Multi-Stage Document Ranking with BERT。
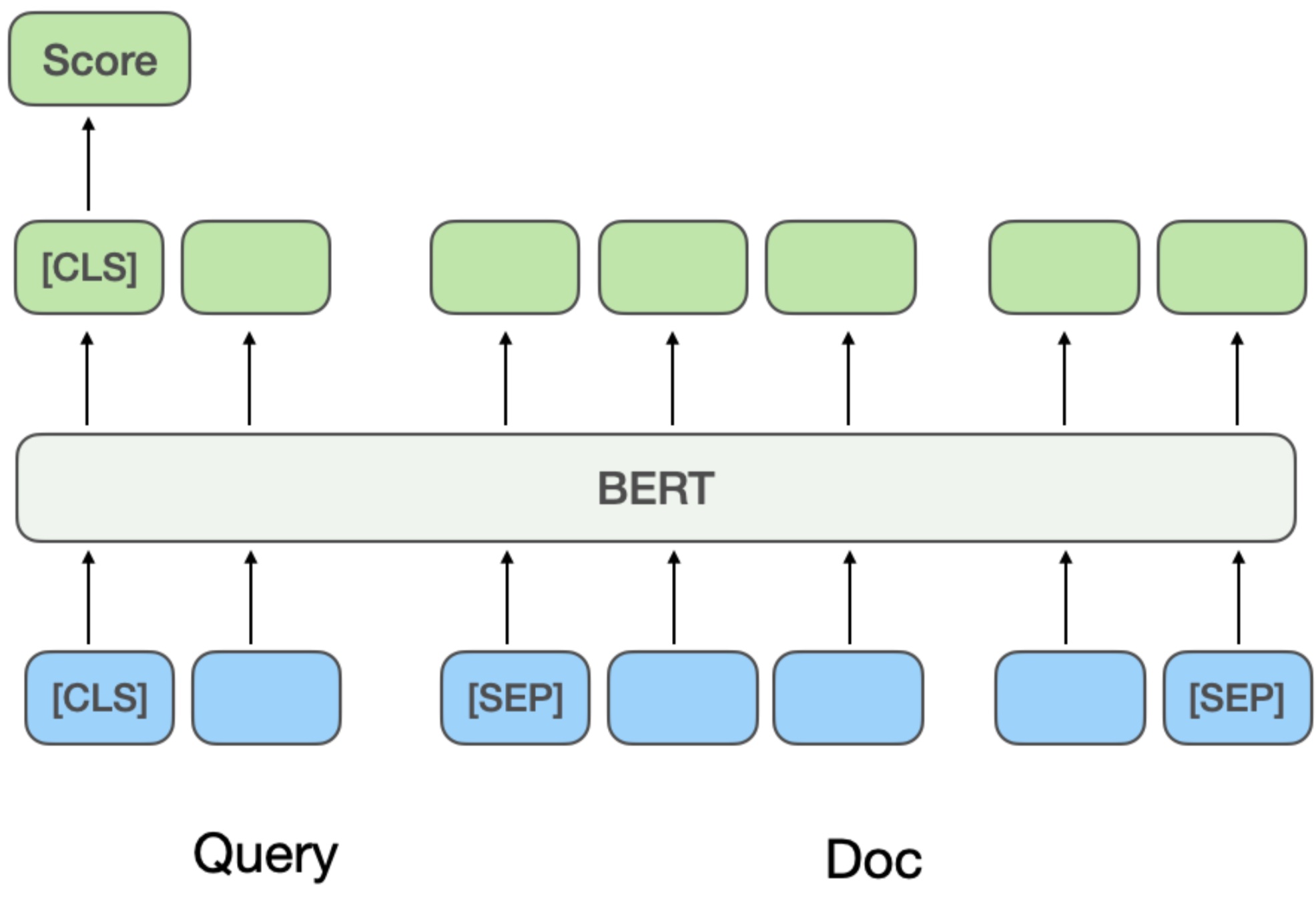
这种方法的优劣刚好跟 representation-based 方法相反了了,优点是匹配精度高,能捕捉非常细粒度的词语交互关系和深层语义信息;但同时计算开销巨大。线上服务时需要将 Query 和 Doc 实时拼接并送入大型模型进行前向计算,延迟高,对性能挑战大
多阶段训练
建模需要解决几个基础问题,包括训练样本获取、特征构造、模型指标等。而在相关性建模任务中,直接的领域打标数据获取是有不小成本的,所以需要考虑因此会通过多阶段训练尽量在成本可控的情况下,提升模型效果
- 训练样本获取
由于相关性标准是平台制定且会频繁变化的,因此相关性训练样本的 label 不像 ctr、cvr 这类任务有明确的 ground truth,而是依靠人工标注。且相关性标准如果有变化,label 也可能会有变化,因此实际中针对某个特定领域,相关性模型训练样本的获取的成本是比较高的
因此在实际的训练过程中,往往是结合预训练模型 + 大量容易获取 label 的相关领域数据先做一轮数据,然后再利用上面提到的人工标注的数据来做进一步的 finetune。以上面大众点评的文章为例(其他的领域其实大同小异),会先采用用户点击和负采样数据进行第一阶段领域适配的预训练(Continual Domain-Adaptive Pre-training),然后采用人工标注数据进行第二阶段训练(Fine-Tune)
第一阶段训练:这个阶段将用户是否点击来作为 “是否相关” 的 label,这种做法能够低成本获取很多训练样本。但如果直接将点击样本用于相关性判断会存在较大噪声,因为用户是否点击后受到很多信息的影响(最常见的就是位置信息,越靠前的越容易被点击,靠后的不被点击,但这并不是因为相关性问题),所以做法是引入了多种特征和规则来提高训练样本的准确率。具体规则如下
对于正样本获取,通过统计是否点击、点击位次、最大点击商户距用户的距离等特征筛选候选样本,将曝光点击率大于一定阈值的作为正例;对于负样本的获取,将位于点击 doc 之前且点击率小于阈值的 doc 才做为负样本,同时采用随机负采样的方式可以为训练样本补充简单负例,但考虑随机负采样时也会引入一些噪声数据,所以利用人工设计的规则对训练数据进行降噪:如当 Query 的类目意图与 doc 的类目体系较为一致时或者与 doc 名高度匹配时,则将其从负样本中剔除
第二阶段训练:第二阶段就是常见的 fine-tune 训练了,固定住底层参数,利用人工标准的更准确的 label 来对顶层参数做微调。但是不同样本被标注的价值也是不太一样,如模型本身就能很好判断的 easy pair,不如那些模型判断不清楚的 hard pair,因此在人工标注上,点评不是随机送一批样本给人工去标注的,而是通过难例挖掘和对比样本增强方式生产大量高价值样本交给人工去标注
- 难例挖掘:包括 1)将用户点击过但线上旧版模型判定为不相关的作为难例;2)通过边缘采样的方式挖掘具有较高不确定性的样本,如抽取模型预测得分在阈值附近的样本;3)模型或人工识别困难的样本,用当前模型预测训练集,将模型预测结果与标注标签不一致的样本,及人工标注标签有冲突的样本类型重新送标
- 对比样本增强:借鉴对比学习的思想,为一些高度匹配的样本生成对比样本进行数据增强,并进行人工标注确保样本标签的准确率。通过对比样本之间的差异,模型可以关注到真正有用的信息,同时提升对同义词的泛化能力,这里给了一个这样的例子
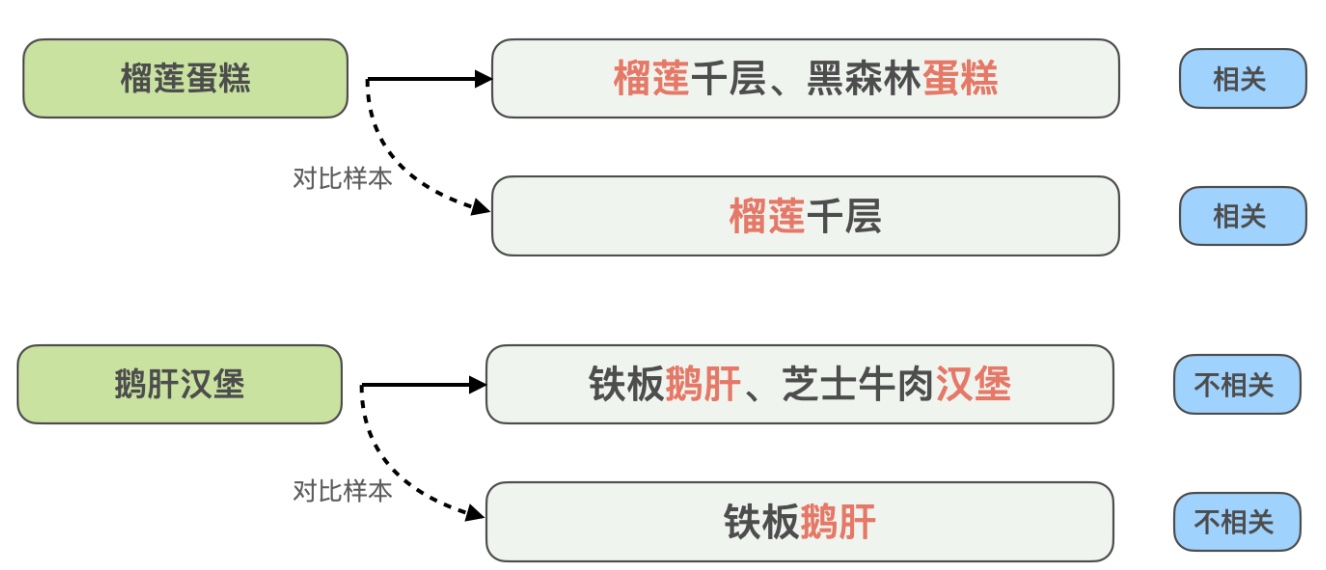
这里 query “榴莲蛋糕” 与推荐的 “榴莲千层、黑森林蛋糕” 是相关的,但 query “鹅肝汉堡” 与 “铁板鹅肝、芝士牛肉汉堡” 是不相关的,为了增强模型对这类高度匹配但结果相反的 case 的识别能力,文章的方法是构造了 “榴莲蛋糕” 与 “榴莲千层”、“鹅肝汉堡” 与 “铁板鹅肝” 这两组对比样本,去掉了与 query 在文本上匹配但对模型判断没有帮助的信息,让模型学到真正决定是否相关的关键信息,同时提升模型对 “蛋糕” 和 “千层” 这类同义词的泛化能力
- 特征
由于相关性是一个相对客观的标准(即给定一个 query 和 doc,后验的 label 是明确的),受 context 信息影响比较小(如位置信息、上下文信息),或者说在 query 和 doc 不会因为换了位置等信息,相关性就会发生变化。因此相关性模型使用的特征相对来说也比较简单,query 特征一般是原始的 query 文本,doc 特征一般是 doc 的多模态信息(如 title、image)和 meta 信息(如 doc 所属的类别、类目等)
而随着大模型的广泛使用,也发展出了利用大模型来构造额外的 query 和 doc 特征的路线。以 query 为例,基本的做法就是基于 query 构造 prompt(如基于 query 和各个平台搜索出来的结果),然后让大模型总结输出更准确和详细的 query summary,然后把这个 query summary 作为额外的 query 特征输入给相关性模型
在业界上一般是基于 RAG(Retrieval-Augmented Generation)来完成这个步骤,RAG 结合了检索(Retrieval)和生成(Generation)两种技术。基本的工作原理是当模型接收到一个 query 时,首先在一个大型的索引中检索相关的文档或信息片段,检索是基于相似性度量完成的,目的是找到与 query 最相关的信息,然后模型使用检索到的文档作为额外的上下文信息输入来生成内容,生成的这一步通常是由大模型来完成。如下图所示是一个基础的流程
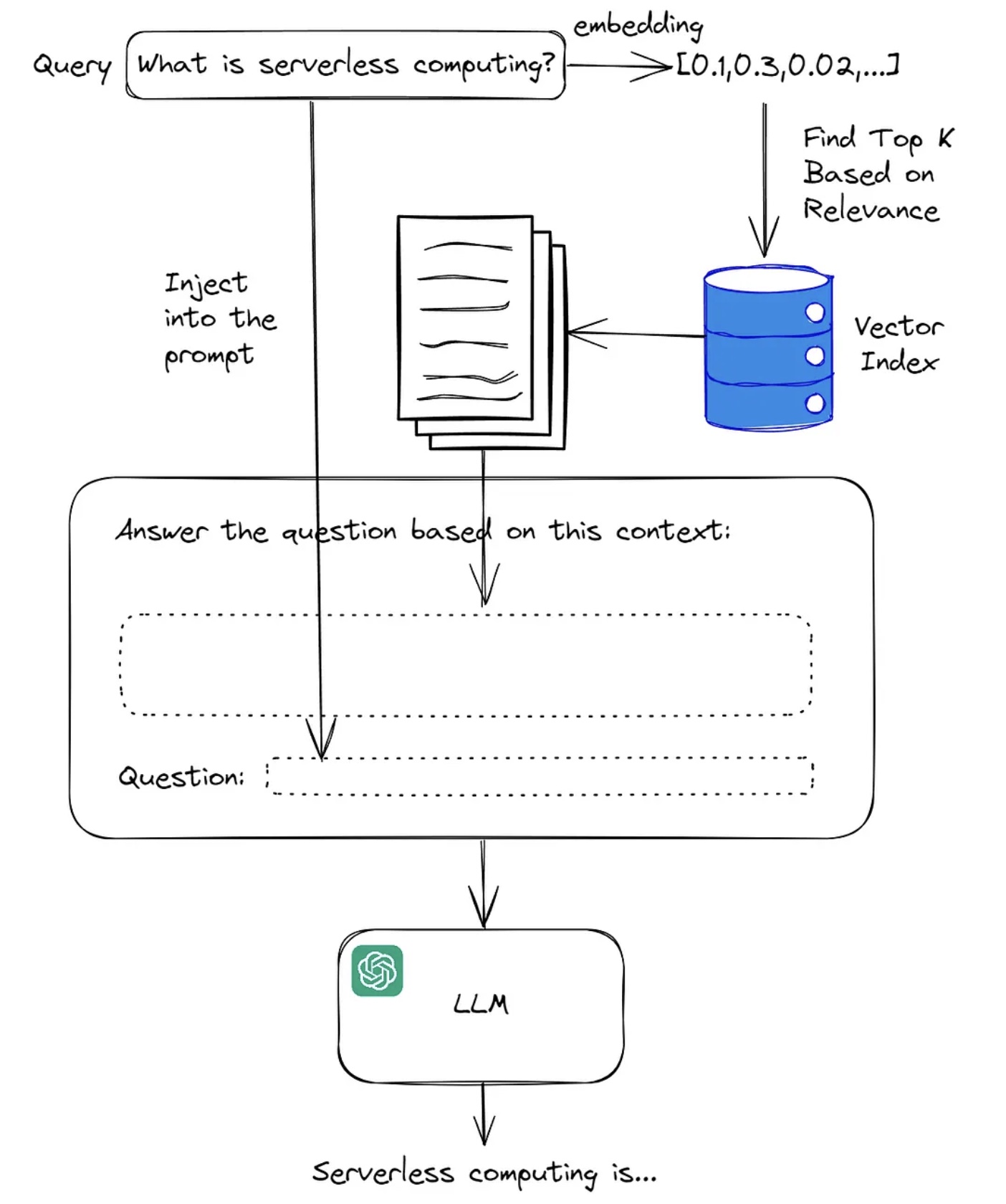
RAG 技术通过给 LLM 更详细的输入,能缓解 LLM 的幻觉问题,也通常被应用在特定的垂直搜索的领域。关于 RAG 更详细的介绍,可以进一步参考这篇文章 大模型 RAG(检索增强生成)含高级方法
排序机制
有了相关性预估分后,需要考虑的就是在线上如何应用这个预估分了。在系统中往往通过以下两个手段来保证相关性:相关性门槛和排序公式增加相关性项
- 相关性门槛:固定值,用于过滤低相关性广告候选
- 排序公式增加相关性项:动态变化值,控制投后相关性目标达标
搜索的相关性根本的目标是保证约定的 badcase 率约束不超,而相关性分的 label 如果定义为是否 badcase,那预估分的物理含义即为是否 badcase 的概率,就成了一个很常规的二分类任务了。则当模型预估准确的时候,通过控制投后的预估均值等于某个目标,即可控制 badcase 率在固定值附近。如 badcase 目标是 5%,相关性预估值准确情况下,让相关性预估均值保持为 0.95,即可达成这个目标
那这个在系统中的排序机制应该是怎么样的,下面会针对这个问题提供一个解决思路
最优排序公式
首先是最优排序公式的推导,通过下面的推导把问题形式化,这里以广告场景最大化 ecpm 为例
假设有 \(n\) 条请求,第 \(i\) 条请求曝光的广告的相关性预估分位 \(predict\_rel\_score_i\),广告价值为 \(ecpm_i\),相关性均值的目标为 target。则需要求解的问题的可形式化表达为如下形式(其中决策变量 \(x\) 为广告选择策略)
\[\begin{align} \max_x &\sum_{i=0}^{n-1} ecpm_i \\ s.t. \frac{1}{n} &\sum_{i=0}^{n-1} predict\_rel\_score_i=target \end{align}\]
问题建模
由于每条请求往往会有多条广告,上述问题可进一步细化到如下形式
假设每个请求 \(i\) 有 \(m_i\) 个候选广告。对于广告 \(k\) 在请求 \(i\) 上,定义:
- \(ecpm_{ik}\):广告的 eCPM 值
- \(s_{ik}\):广告的相关性预估分数(即 \(predict\_rel\_score\))
- \(x_{ik}\):引入二元决策变量,\(x_{ik}=1\) 表示在请求 \(i\) 上选择广告 \(k\),否则 \(x_{ik}=0\)
则问题可表述成如下形式
\[\begin{align} \max &\sum_{i=0}^{n-1} \sum_{k} x_{ik} \cdot ecpm_i \\ s.t. &\sum_{i=0}^{n-1} \sum_{k} x_{ik} \cdot s_{ik} = (\sum_{i=0}^{n-1} \sum_{k} x_{ik}) \cdot target \\ & x_{ik} \in \{0,1\} \quad \forall i,k \end{align}\]
问题求解
1. 拉格朗日松弛
由于约束是等式且全局,使用拉格朗日乘数法将约束融入目标函数。引入拉格朗日乘数 \(\lambda\),构造拉格朗日函数 \(L\):
\[\begin{align} L(\mathbf{x}, \lambda) &= \sum_{i=0}^{n-1} \sum_{k} x_{ik} \cdot \text{ecpm}_{ik} + \lambda \left( \sum_{i=0}^{n-1} \sum_{k} x_{ik} \cdot s_{ik} - (\sum_{i=0}^{n-1} \sum_{k} x_{ik}) \cdot \text{target} \right) \\ &= \sum_{i=0}^{n-1} \sum_{k} x_{ik} \cdot (\text{ecpm}_{ik} + \lambda \cdot (s_{ik} - \text{target})) \end{align}\]
这里的 \(\lambda\) 可以解释为相关性约束的 “影子价格”,表示每单位相关性分数变化对总 eCPM 的边际影响,则最大化 \(L\) 等价于最大化
\[\begin{align} \max L(\mathbf{x}, \lambda) \iff \max \sum_{i=0}^{n-1} \sum_{k} x_{ik} \cdot (\text{ecpm}_{ik} + \lambda \cdot (s_{ik} - \text{target})) \end{align}\]
2. 问题分解
对于每个请求 \(i\),最大化 \(\sum_{k} x_{ik} \cdot (\text{ecpm}_{ik} + \lambda \cdot (s_{ik} - \text{target}))\),等价于选择广告 \(k\) 使得 \(\text{ecpm}_{ik} + \lambda \cdot (s_{ik} - \text{target})\) 最大
\[\begin{align} k_i^* = \arg\max_{k} (\text{ecpm}_{ik} + \lambda \cdot (s_{ik} - \text{target})) \end{align}\]
因此,最优决策是对于每个请求 \(i\),独立选择广告 \(k\) 以最大化以下线性组合,同时也是每条请求的排序公式
\[\begin{align} score_{ik}=\text{ecpm}_{ik} + \lambda \cdot (s_{ik} - \text{target}) \end{align}\]
3. \(\lambda\) 求解
在数学上,\(\lambda\) 是拉格朗日乘数,通过求解约束方程获得。实际系统中,\(\lambda\) 可以通过迭代方法调整(如二分搜索、梯度下降或在线学习),如可以使用二分搜索方法(因为 \(s_i(\lambda)\) 是关于 \(\lambda\) 是单调递增的函数),步骤如下
- 初始化 \(\lambda_{low}\) 和 \(\lambda_{high}\)
- 对于每个 \(\lambda\),计算所有请求的选择(最大化 \(\text{ecpm}_{ik} + \lambda \cdot s_{ik}\)) 并计算平均 \(s_i\)
- 如果平均 \(s_i > \text{target}\),则减小 \(\lambda\)(降低相关性权重);反之增大 \(\lambda\)
- 重复直到平均 \(s_i\) 收敛到 target
上述方法需要我们获取的所有的流量和候选才能执行,相当于回放过去一段时间的流量得到的历史最优兑换比 \(\lambda\)。但这跟最优出价比较类似,实际中比较难直接应用。因为这里有两个前提:(1)获取到当天所有流量的数据(2)改变实际竞胜的广告不会影响竞价环境。在实际中这俩往往是难以满足
更常见的实际做法是基于过去一段时间搜集的相关性预估值均值,然后基于 pid 来做实时调控调整 \(\lambda\) 的值,pacing 的目标就是相关性均值等于 target。这部分其实跟出价调控比较类似,与计划最优出价类似,这也导致了实际的兑换比与理论最优兑换比有 gap,需要通过各种手段逼近理论最优的兑换比
逼近理论最优
如果进一步分析,会发现实际通过 pid 等控制器调控的方式,相较于流量回放直接解决最优化问题,差异在于调控过程中是否感知到了流量价值即 ecpm
因为在解决最优化问题时,有最大化 ecpm 这一目标在约束求解过程,会去寻找刚好满足 target 达成的 \(\lambda\)。但在实际的控制器调控中,只能感知到当前相关性均值是否达标了,当相关性不达标的时候会把 \(\lambda\) 调得非常大,导致 ecpm 项在排序中发挥的作用非常小,这就导致了 ecpm 非最优
比如说在两个连续的时间片内,前一个时间相关性是不达标的状态,但有高 ecpm 的候选,这个时候只考虑相关性,会把 \(\lambda\) 调的很大,导致高 ecpm 候选出不去(因为相关性项占了主导),而接着下一个时间片相关性有缓解了(因为前一个时间片出了高相关性广告),但候选没有高 ecpm 的,此时降低相关性项的权重,但出的广告 ecpm 也不是最优的了;但如果反过来,在前一个时间片降低 \(\lambda\) 后一个时间片升高 \(\lambda\),是可以做到打平相关性最大化 ecpm 的,而这需要的就是调控感知流量价值
在调控 \(\lambda\) 过程中感知到流量价值即 ecpm,最直观的就是用过去一段时间 \(t\) 内搜集到的流量和广告候选,然后直接通过上面提到的二分法直接求解这个最优化问题,求得最优的兑换比 \(\lambda^*\),用作下一个时间片的兑换比。但这里有一个比较强的假设是过去过去一段时间 \(t\) 的流量和候选分布,跟下一个时间片的类似(或者说差异不大),才能有效,否则约束比较难达成
除了上面的方法,还有一种更直观的方法,就是在调控过程中直接基于流量价值动态调整兑换比。如果把流量按照价值和相关性两个维度划分,可以划分为如下四个象限
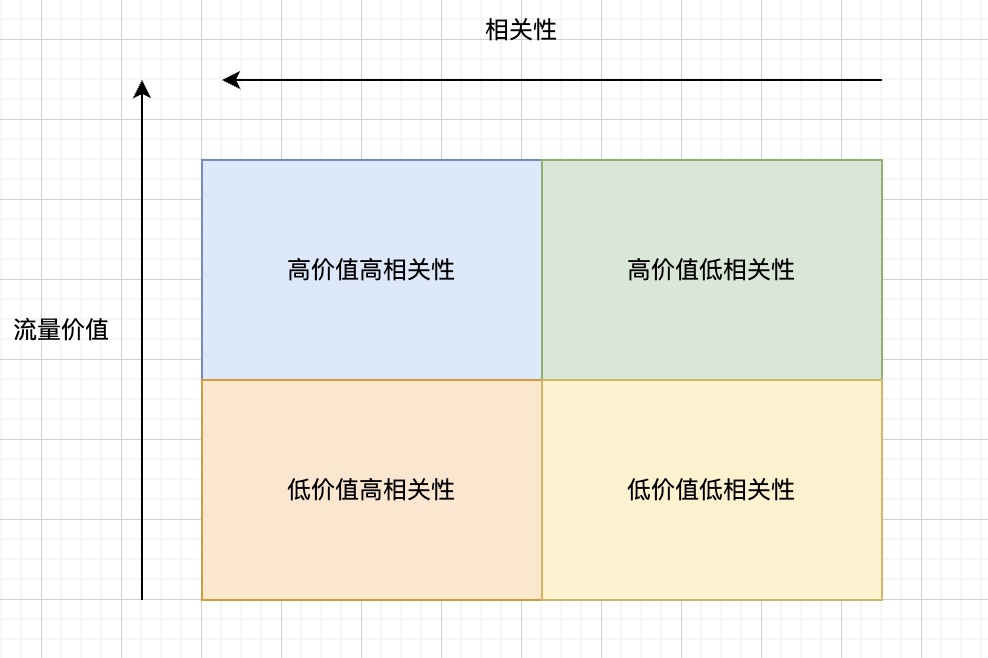
对于这四类流量,如果直观来看,可以先验给出如下的兑换原则
(1)高价值高相关性的流量,降低兑换比,尽可能多出高 ecpm 广告
(2)低价值高相关性的流量,提高兑换比,尽可能多出高相关性广告来填补高相关性
(3)高价值低相关性的流量,降低兑换比,但兑换比要比(1)更高,防止相关性不达标
(4)低价值低相关性的流量,提高兑换比,兑换比(2)要更高,尽量不出广告
这里的做法跟前面的理论最优推导出来的结论 “全局最优的兑换比是一个固定的 \(\lambda\)” 有点矛盾。因为这里相当于是给高价值流量和低价值流量不同的兑换比,而不是全局统一的;但事实上理论最优的假设(看到所有流量)是没法满足的,而我们当前本身就是在做理论最优解的逼近,所以不一定要遵循理论最优的固定的 \(\lambda\) 的这个结论
另外这个方法有效也有两个重要假设:1)高价值流量损失的相关性可以从低价值流量上找补回来;2)单位相关性在高价值流量上的兑换效率比低价值流量的更高。1)比较好理解,因为如果找补不回来那相关性就无法达成,而 2)指的是 ecpm 和相关性分数的分布在高低价值是不一样的,或者更直观地说:在高价值流量上获取单位相关性损失的 \(\Delta ecpm\) 会比低价值流量更大,而这其实取决于实际的库存分布(即 ecpm 和相关性分的分布),从实际系统来看,这个假设成立的概率还是不小的
另外,在实际调控中,需要考虑对这些兑换比调整后,大盘的 target 是能达到的。从这个角度来看,其实方案 2 比方案 1 是更能达成这一点的,因为可以基于统一的调控系数来做扰动。方案二的解决思路类似出价中的 “保浅优深” 的扰动策略,在保证大盘 target 目标达成的前提下,基于流量价值对 \(\lambda\) 做扰动;但是与出价不同的是,出价往往是在计划维度做这个事情,但相关性是大盘维度的,没法做在计划维度,一是 target 是大盘约束,没法很好拆解到各个计划上,二是做在计划维度上也不是最优的,因为做在计划上要求每个计划都有一个 target,这样计划之间就不好做兑换了,或者说要约束更多了,求解空间更小了。关于出价问题上类似的解决思路,可以参考这篇文章《Bid Optimization by Multivariable Control in Display Advertising》
小结
本文从搜索与推荐场景的差异出发,探讨了相关性建模的技术演进与排序机制中的最优控制策略,试图为这一经典问题提供系统性的解决思路。搜索场景的强意图特性决定了相关性问题的特殊性:与推荐场景的 “无目的性浏览” 不同,用户搜索带有明确预期,这要求结果必须精准匹配查询意图。从技术视角上可以分为相关性建模和排序机制两部分
在相关性建模中,基本的迭代经历了从文本匹配到深度语义匹配的演进。当前主流方法可分为基于表示(Representation-based)和基于交互(Interaction-based)两类范式,两者在精度与性能间各有权衡。而引入预训练模型及 RAG 技术后,模型对语义的理解深度和泛化能力得到了显著提升。关于相关性建模有两点值得关注,一是基于大模型的语义理解与生成:大语言模型(LLM)在语义理解、意图推理和内容生成方面展现出强大能力,未来有望深入应用 LLM 进行查询意图的深层解析、扩展与归一化,甚至直接生成或增强相关内容摘要,进一步提升相关性判断的准确性和可解释性;二是个性化相关性理解:搜索意图有群体共性,但亦存在个体差异;虽然当前的相关性与 context 不相关,但未来的相关性模型可能需要更好地融合用户个性化上下文(如历史行为、实时偏好),在保证基础相关性的前提下,提供更契合个体需求的精准结果
在排序机制中。通过最优化问题形式化推导了带相关性约束的排序公式 \(score =\text{ecpm} + \lambda \cdot \text{rel_score}\)。其中的拉格朗日乘数 \(\lambda\) 可视为相关性约束的 “影子价格”,通过调控 \(\lambda\) 可实现相关性目标的达成与 ecpm 最大化间的平衡
当前 \(\lambda\) 调控多基于大盘均值,难以感知流量价值差异。理想状态应实现分流量价值层的精细化调控,对高价值高相关性流量降低 \(\lambda\) 以提升 ecpm,对低价值高相关性流量提高 \(\lambda\) 以保证相关体验。同时需要考虑在不破坏大盘目标的前提下实现这种动态调控
搜索广告的相关性,归根结底是在用户意图、广告主诉求和平台价值三者间寻求最佳平衡的艺术与科学。它既需要深入的技术建模与算法优化,也离不开对用户搜索心理和广告主业务目标的深刻洞察。未来的搜索广告系统,或许将更加智能与自适应,能够动态感知不同场景、不同用户对相关性的差异化期望,并精准调控商业与体验的平衡点